基于极值理论的干扰聚集系统突发事件风险分析

韩正强 邓景毅

一、引言

当一个国家的人均GDP进入3000美元区域时，各种突发事件会集中爆发，我国每年由此造成的经济损失达到GDP总量的5%，加强对突发事件的应急管理已经成为我国各级政府的重要工作内容和目标。针对各类突发事件进行科学的风险分析，有利于提高应急决策水平，优化应急资源配置，进而降低灾害损失，实现组织的应急管理目标。

在灾害的演化研究中，人们往往更多地关注事件的异常性，如病毒基因的变异，两架飞机同时改变着陆机场而导致的空难。但是，随着研究的逐步深入，人们越来越认识到：灾害的损失与其产生的原因不存在比例关系，一些大的灾难往往是由于微小的干扰引起的，如导致美国航天飞机失事的O型圈事件；几乎导致美苏核战争的熊事件。对于该类事件，Perrow（1981）称之为正常事件（Normal Accident）。因此，在突发事件的研究中，我们可以界定这样一类系统，在这类系统中，存在大量的干扰，其发生的数量是随机的，这些干扰如果得不到及时处理，会对系统的生存造成重要影响，当这些干扰不断集聚，达到一定阈值时（本文的第三部分应用系统动力学仿真方法验证了阈值的存在性），将导致突发性的灾害事件，我们称之为干扰聚集系统。

本文以干扰聚集系统为研究对象，首先阐述了干扰聚集系统的基本概念，然后应用系统动力学仿真模型验证了干扰聚集系统中阈值的存在性；进而应用极值理论对干扰聚集系统突发事件的发生概率进行定量分析；最后对全文进行了总结，并展望了未来的研究方向。

二、相关文献

陈长坤等（2009）对危机事件的演化进行了分类；罗成琳等（2009）认为突发事件演化存在生命周期；孙康等（2006）利用一般模仿者动态模型和博弈论分析了群体性突发事件的演化过程；Rudolph等（2002）进行了灾害动力学的研究。从目前的研究来看，对于复杂系统（特别是包含人类行为的复杂系统）的演化研究，主要以定性分析居多，定量分析较少。

突发事件风险分析大部分针对某一专门领域，而且自然领域居多，社会领域较少。其中，季学伟等（2009）应用概率函数、层次分析等方法确定了火灾、地震等原生灾害引起的次生事件的发生概率；Sun等（2009）应用复杂神经网络对岩层突裂进行了预测；GuiKema（2009）利用统计学习理论对自然灾害导致的关键基础设施失效进行了风险分析；Iman和Eyke（2007）则采用基于模糊概率的方法对自然灾害进行风险评估；Jiang等（2009）对马来西亚的洪灾地区进行了实证分析，证实了模糊数学理论在洪灾风险评估中的有效性。关于社会系统的突发事件风险定量分析未见相关文献。

三、干扰聚集系统阈值的系统动力学仿真分析

干扰聚集系统首先是一个社会系统，控制人员在系统中负责处理各种干扰，但是单位时间内人的处理能力是有限的，当人的处理能力达到极限而干扰仍然在不断增加时，系统将发生灾难崩溃；其次，干扰聚集系统中的要素众多，各种要素都存在失效的可能性，一旦失效或者未按照人们的预期工作，将产生各种干扰，等待系统控制人员进行处理以恢复正常；最后，系统产生的干扰，人们在理性的条件下能够对其进行处理，但是，寻找干扰产生的根源以及处理这些干扰需要时间和其他资源（包括物质和信息），在时间压力和资源有限的情况下，会导致处理失误。航天飞机、核电站、大型计算机网络均可以看作这类系统。

干扰的聚集导致系统的突发灾害事件。耶鲁大学社会学家Perrow（1999）指出，这些干扰是不可避免的，而且连续不断地以一种常态的形式发生。Rudolph（2002）则强调干扰的数量是导致突发灾害的重要因素。当系统中的干扰不断发生时，系统控制人员分析和解决这些问题，使系统稳定在某一平衡态，远离临界点。控制人员的问题解决能力（行为）与自身的能力有关，也与其所处的外部环境压力有关，行为与外部环境压力之间的关系可以用Yerkes-Dodson曲线描述。由于干扰聚集系统中干扰在某一时刻的发生数量是随机的，而控制人员的行为也难以使用数学函数进行精确定义和描述，因此通过精确的确定性数学模型求解干扰聚集系统阈值显得非常困难，而建立基于系统动力学的仿真模型是可供选择的方法。依据Forrest（1961）和Sterman（2000）提供的系统动力学方法，在Rudolph（2002）的基础上，本文针对干扰聚集系统完成了系统动力学仿真建模和分析。

（一）模型的假设

干扰聚集系统是复杂大系统，考虑所有与突发事件相关的因素是不现实的。为使模型便于系统仿真，并且尽可能与实际相吻合，本文作如下假设：

1）模型主要考察干扰数量导致的突发事件，而由于干扰相互作用引起的异常事件（NovelEvent），模型不予考察。主要原因在于：首先模型的目的是验证和确定干扰导致突发灾害在数量上的阈值；其次干扰相互作用导致异常事件的机理目前尚不能确定，更无法进行定量分析；最后控制人员能否处理异常事件以及所占用的资源难以确定，这将导致后续模拟仿真无法进行。因此，尽管某些突发事件的主要因素是异常事件，但本模型不进行分析。

2）压力是单位时间内发生的干扰总和与控制人员的处理能力的比值。一旦单位时间内干扰的发生频率大于控制人员的处理能力，就会对控制人员造成压力。控制人员承受的压力与处理能力的关系遵循Yerkes-Dodson法则。

3）控制人员在处理干扰时会发生错误，错误以一定的概率发生。错误发生后需要重新再处理，处理的时长不发生变化。不考虑处理错误带来的后续关联影响。

（二）系统动力学流图

系统动力学流图的相关变量如下：

Interruption Arrival Rate：干扰到达率（流）；

Interruption Resolution Rate：干扰处理率（流）；

Interruption Pending：未处理的干扰（水准）；

Error：由于不正确处理产生的错误（流）；

Error FeedBack：错误反馈（辅助变量）；

Desired Resolution Time：系统期望处理时间（常量）；

Desired Resolution Rate：系统期望处理率（辅助变量）；

Normal Rate：控制人员的正常处理率（常量）；

Stress：压力（辅助变量）。

其中，压力和干扰的处理率之间的关系见下图。鉴于篇幅，相关的系统动力学方程和初始设置略。

图1 扰聚集系统系统动力学流图

（三）系统仿真结果与分析

基于以上系统动力学方程和系统动力学流图，使用STELLA 9.0软件进行系统动力学仿真（STELLA 9.0是iSee Systems公司的系统分析软件之一，是目前商业领域应用最为广泛的系统动力学软件之一）。在仿真过程中，脉冲分析是常见的系统输入分析方法。我们对干扰到达率设置了脉冲，第一次设置的脉冲值为正常值的200%，第二次设置的脉冲为正常值的300%，脉冲持续时间均为1单位。仿真结果见图2（为便于两次仿真的比较，本文采用数据表方式进行仿真输出后，应用EXCEL2003绘制仿真结果图）。

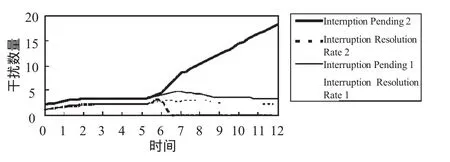
图2 两次不同脉冲输入的系统仿真结果

基于以上系统仿真结果，我们可以得到以下结论：

1）当脉冲值比较小时，系统具有自我调节功能，经过一段时间后由于脉冲导致的对系统的影响将逐渐减小直至消失。

2）当脉冲值比较大时，系统将丧失自我恢复功能，系统中的干扰将不断积聚，直至最后系统崩溃。显然，在此二值之间存在一个阈值θ（例中，脉冲的阈值为5.4左右），当脉冲越过θ时，系统无法自我恢复。

3）从干扰曲线来看，其曲率的极性并非一直保持不变。存在临界时刻，在此时刻之前（大致对应图中第7单位时间），系统均有可能恢复至稳定态。因此，在处理突发事件时，可以依据此时刻作为参考来判断是应该放弃系统以保存力量还是全力以赴使系统恢复正常。

4）在高压力下，控制人员干扰处理率的急剧下降是导致曲线尾部上翘的重要原因。通过各种训练，提高控制人员在高压力下的处理能力可以改善阈值。

依据具体环境，应用各种随机数发生器产生符合某种分布（如泊松分布）的随机数进行仿真，其结果将更加贴合实际。鉴于本部分的目的在于——证明干扰聚集系统中干扰阈值θ的存在性以及应用系统仿真确定阈值θ的可行性，本文对此不作深入探讨。

四、基于阈值的干扰聚集系统风险分析模型

通过系统动力学仿真确定的干扰聚集系统的阈值，为分析干扰聚集系统突发事件的发生概率及其风险分析提供了基础。正常情况下，在某一时间段内，超过某一阈值θ的概率应该非常低（否则这一系统会不断的发生崩溃），我们可以将其认为是极端事件。极值理论是针对这些极端异常事件进行统计分析的较为有效的工具。

（一）模型的假设

为计算和求解干扰聚集系统突发事件的发生概率和进行风险分析，在第三部分假设的基础上，增加如下假设：

1）完成干扰的处理后，将形成新的干扰聚集系统。新系统的任意时刻干扰发生的数量与原系统具有相同的分布，即底分布保持不变。

2）单位时间段内，观测到的干扰发生数量的极值是独立的。

上述假设使系统满足极值理论的应用条件。

（二）基于阈值μ的极值分布

经典的极值模型所使用的数据是某一组或者一个区段的若干数据中的最大值或者最小值，这将导致这些数据中包含的信息不能被充分利用。因此，一般考虑超过某一阈值μ的观测值，这些观测值的极限服从Pareto分布。由于此处的阈值与导致干扰聚集系统突发事件的阈值是不同的概念，因此分别使用μ和θ表示。Pareto分布定义如下：

假设xt（t=1，2，…n）为随机变量X在时刻t的观测值，将各观测值按降序排序得xi（i=1，2，…n），其中x1≥x2…≥xn，则有：

其中，μ∈R为位置参数，σ>0为尺度参数，ξ∈R为形状参数。

通过变换可以得到，干扰聚集系统突发事件的概率为：

若需要控制p，以使突发事件的概率控制在一定的范围内，则其对应的分位数为：

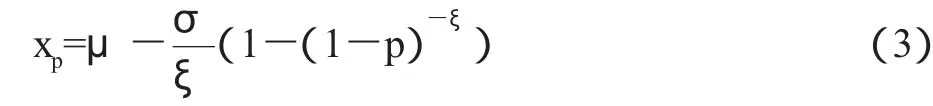
当广义Pareto分布可以作为超过阈值μ超过量的有效近似时，那么对于一个更高的阈值θ的超过量也服从广义Pareto分布。两者的形状参数ξ相同，尺度参数存在以下关系：

由此可知，平均超出量函数为：

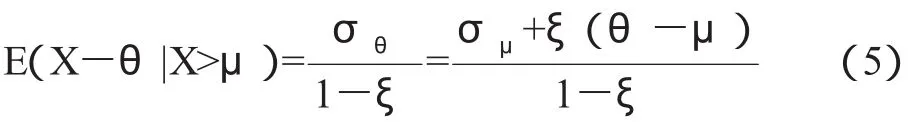
以上各式中，（2）式用于确定系统突发事件的发生概率；（3）和（5）用于确定系统风险和对系统干扰处理率的改进。

（三）阈值μ的选择

阈值μ的选择对于整个模型的建立至关重要。取值太大，会导致超过量太少，使得参数估计量的方差变大；取值太小，则容易产生有偏的参数估计。现有的μ值确定方法有：Hill法；平均剩余寿命图法；二次子样试算法等。

（四）参数的估计

阈值模型的常用参数估计方法包括：极大似然估计和回归方法。其中，极大似然估计具有良好的性质，被广泛使用。依据广义Pareto分布的定义，容易得到其对数似然函数为：

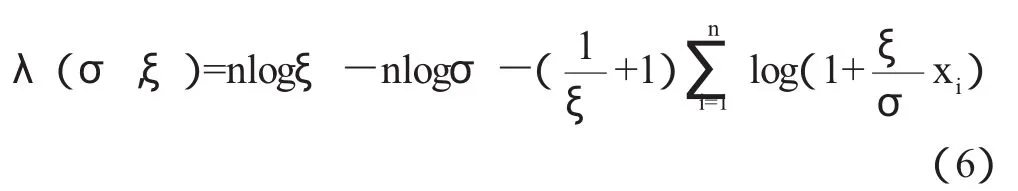
通过数值方法可以求解极大似然估计σ，ξ。

（五）数据分析

1.数据说明

本文选取来自某集团公司的资讯管理部门1998－2000年的数据作为原始数据（该时间段内，资讯管理部门的设备数量基本维持稳定）。部门负责整个公司信息设备的维修和维护工作，员工21人，其所负责维修和维护的信息设备共计3771台（件），包括各种型号的计算机、软件系统（ERP系统、电子邮件系统、考勤系统等）、网络设备、服务器、通讯设备等。将每天发生的设备故障视为各种干扰，这些干扰由资讯管理部门负责处理和解决，干扰得不到及时处理将导致公司的各级管理部门和生产部门的工作延误和决策失误，给公司造成巨大损失。计算机病毒在局域网范围内的大量传播以及网络拥塞造成的电子邮件系统故障、ERP系统故障均可以认为是突发事件。我们假定每一员工的工作能力和技术水平是同质的，这样每一次维修或维护的时长便可作为基本单位进行累加计算。另外，在数据的选取时，我们只确定有效维修或维护时间，依据这一原则对其中的一些数据作了相关的技术处理（如由于缺少相关硬件，需要等待采购，导致名义维修时间大于有效维修时间）。

2.计算结果与分析

图3是针对所有数据作的散点图，统计数据见表1。

!!!"#$%&’

图3 有效时间散点图

依据式（5）可知，如果对于某个阈值μ，超出量分布近似服从广义Pareto分布，则平均超出量函数应该在一条直线附近波动。从图中可以看出，μ应该取在149附近，超出该值的数据有128个。图5和图6的形状参数估计和位置参数估计图进一步验证了该值

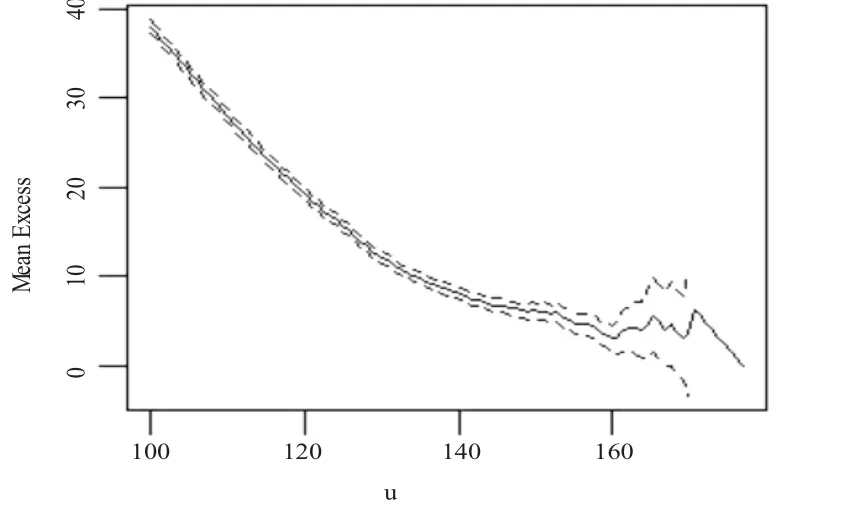
图4 平均超出量分布图

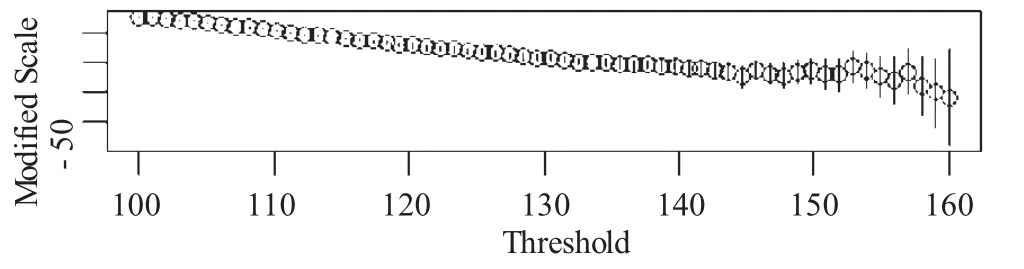
图5 位置参数图

图6 形状参数图

由图5和图6以及计算机分析结果可知：

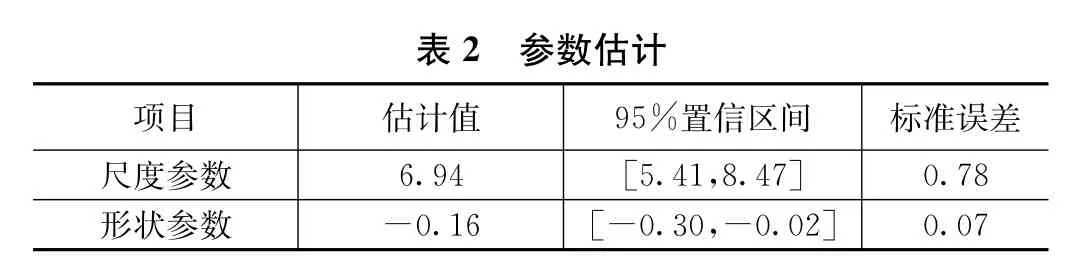
%D ow nLo dddd dddd dddd e ! " #ad Cod e dddd ! " #

图7 概率图

图8 分位数图

图9 重现期水平图

图10 密度图

由此可知，干扰聚集系统突发事件的概率为：

从图7和图8可以看出，样本点均分布在直线附近，因此通过PP图和QQ图均不能否定所拟合的模型；由于ξ<0，因此相应分布的支撑存在有限上界，重现水平图与这一结论吻合。密度曲线的估计也与直方图吻合较好。因此，四个诊断图均支持拟合的Pareto型超阈值分布。

基于以上分析可知，当给定相应的干扰阈值θ，代入（7）式，即可计算出相应的突发事件发生概率，以上例计，若θ取180小时，则突发事件的概率大约为万分之四，重现期为196年左右；若要求该类事件的发生概率小于万分之一，则相应的阈值应该取182.5左右，此时，阈值的增加将导致突发事件的发生概率成倍减少，因此，增加培训，提高干扰处理水平对于降低系统风险效果非常明显。

五、结语

复杂系统演化的深入分析对于突发事件应急管理具有重要意义。微小扰动因素的不断集聚最终导致突发事件的产生。分析表明，通过系统动力学仿真确定干扰聚集系统的阈值，然后依据阈值确定突发事件的发生概率并且进行相应的风险分析是可行的。结论也表明控制人员在压力条件下处理能力的提升将能够成倍地降低系统风险，这与实际相吻合。但是，在干扰聚集系统模型中，各种干扰的相互影响被忽略，而这一因素在某些系统中是至关重要的，如何确定各种干扰的相互影响并建立相应的分析模型是下一步的研究方向。