海南省旅游市场规模预测——基于灰色系统理论的分析

何 彪，朱连心

（1.海南大学 旅游学院，海南 海口 570228；2.海南大学 经济与管理学院，海南 海口 570228）

海南省旅游市场规模预测
——基于灰色系统理论的分析

何 彪1，朱连心2

（1.海南大学 旅游学院，海南 海口 570228；2.海南大学 经济与管理学院，海南 海口 570228）

科学的旅游预测是促进旅游业可持续发展的重要保障，文章将灰色系统相关理论与旅游业相结合，简要介绍了灰色系统GM（1，1）预测模型，并将其运用于区域旅游市场预测中，以海南省为例进行了预测，并获得了较好的预测效果.

灰色理论；GM（1，1）模型；海南；旅游市场；预测

随着海南国际旅游岛战略上升为国家战略，《国际旅游岛建设发展规划纲要（2010-2020）》（下称纲要）于2010年6月8日获得国家发改委的正式批复，标志着海南国际旅游岛建设进入更加深入的操作阶段.在纲要中，制定了到2020年海南接待国内外游客7680万人次的目标.本文试图将灰色系统理论引入到旅游市场规模的预测中，通过建立模型来对海南旅游接待人次数进行预测.

1 预测模型的构建

1.1 灰色系统的概念

系统是指相互依赖的两个以上要素所构成的具有特定功能的有机整体，系统可以根据其信息的清晰程度分为白色、黑色和灰色系统，白色系统是指信息完全清楚的系统，黑色系统是指信息全部未知的系统，灰色系统是介于白色系统和黑色系统之间的系统，即是指部分信息已知、部分信息未知的系统[1].

灰色系统理论认为，任何随机过程都是在一定幅度范围和一定时区变化的灰色量，并把随机过程看成灰色过程.尽管客观系统表象复杂，数据离乱，但它总是有整体功能的，因此必然蕴涵某种内在规律，关键在于如何选择适当的方式去挖掘它和利用它，灰色系统通过对原始数据的整理来寻求其变化规律，包括累加生成、累减生成和均值生成.灰色系统理论所涉及的主要工作之一是用离散数列建立微分方程型的动态模型，即灰色模型（Grey Modle，简称GM）.

1.2 GM（1，1）模型

GM（1，1）模型是将离散的随机数经过一次累加生成算子（记为1-AGO，Accumulating Generation Operator），削弱其随机性，得到较有规律的生成数，然后建立白化式微分方程、解方程进而建立模型.其构建步骤如下.

1.2.1 原始数列

一般以已知研究对象的某种信息数据组为原始数列，将其记为：x（0）=（x（0）（1），x（0）（2），x（0）（3），…，x（0）（n）），式中n表示时间序列.

1.2.2 原始数据累加和均值生成

由于原始数据多为随机，不便直接处理，因此对此进行累加和均值处理，如下：

1）累加生成数列：

通过一次累加，得到以下数列，记为：

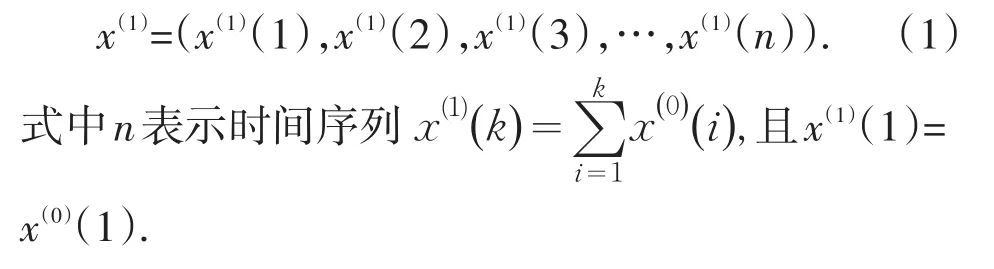
2）均值生成数列：

通过一次均值，得到以下数列，记为：

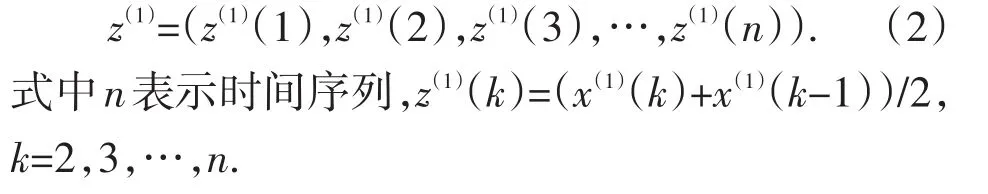
1.2 .3 建立GM（1，1）模型

根据式（1）和式（2）建立一个单序列的一阶线性动态灰色预测模型，如下：

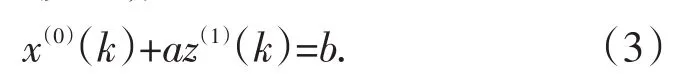
式中a，b为参数，式（3）即为GM（1，1）模型.

1.2.4 GM（1，1）模型的求解

式中，Y是已知数，B是处理后的已知数，θ为待定参数，也即a，b为待定参数.

2）求解a和b：

式

（5）为式（3）的白化方程，即影子方程.

式5的解也称周期响应函数，记为：

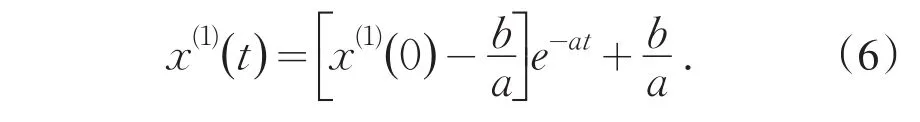
式（6）即预测模型.

3）模型检验：

根据灰色系统理论，一般使用三种检验方式来对灰色模型进行精度检验：残差大小检验、后验检验和关联度检验.残差大小检验式直观的将模型计算值与原始值逐一进行相对误差检验；后验差检验按照残差的概率分布进行检验；关联度检验则属几何检验，它检验的式模型曲线与行为曲线的几何相似程度.最常用的是相对误差检验指标，如下式：

从灰色预测方法原理可知，-a主要控制系统发展态势的大小，即反映预测的发展态势，被称为发展系数；b的大小反映了数据变化的关系，被称为灰色作用量[2]，其中：

当-a＜0.3时，GM（1，1）模型可用于中长期预测，预测精度较高.

当 0.3＜-a＜0.5，GM（1，1）模型可用于短期预测，中长期预测慎用.

当0.5＜-a＜1时，应采用GM（1，1）改进模型，包括GM（1，1）残差修正模型.

当1＜-a时，不宜采用GM（1，1）模型，可考虑其他预测方法.

2 GM（1，1）模型对海南旅游接待人次数的预测

旅游业是海南的重要支柱产业，旅游业收入占海南GDP的比重非常高，旅游业是海南经济发展的重要推动力，表1是海南2000-2009年的年旅游接待人次数.

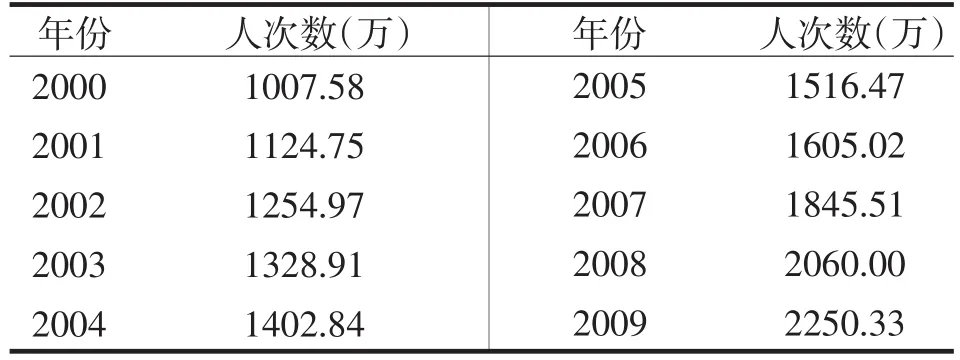
表1 海南2000-2009年旅游接待人次数Tab.1 The visitor's reception amount during 2000-2009 in Hainan Province

2.1 相关数据的处理

设x（0）为原始数据序列，x（1）为x（0）的 1-AGO 序列，z（1）为x（1）的紧邻均值生成序列，ε为x（0）的光滑度检验值，ε的计算公式如下：

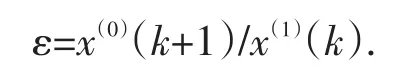
这样得到处理后的数据，见表2.

2.2 构建矩阵与确定参数

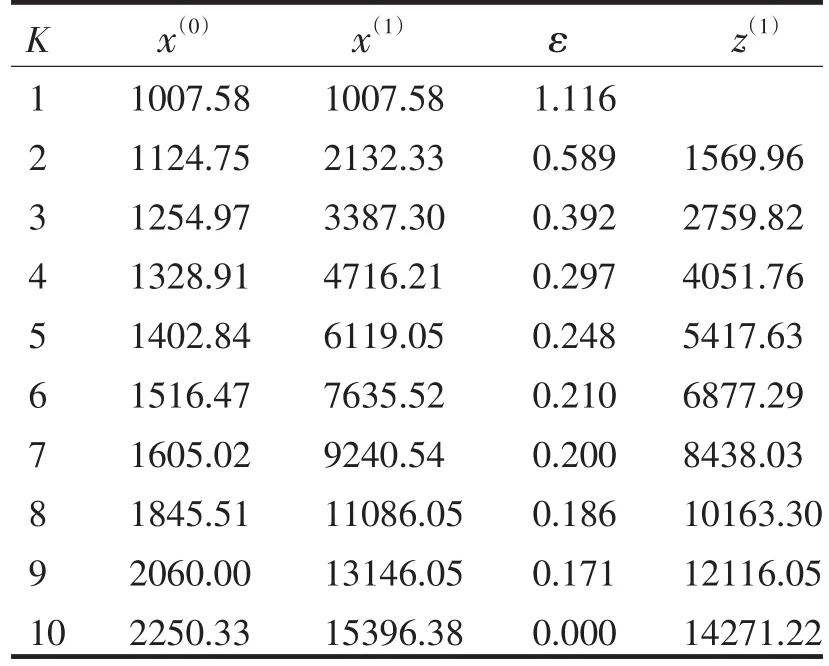
表2 处理后的数据序列Tab.2Once accumulating generation operator and mean generation operator sequence

解白化方程，令X（1）（0）=X（0）（1）=1007.58，得到预测方程：

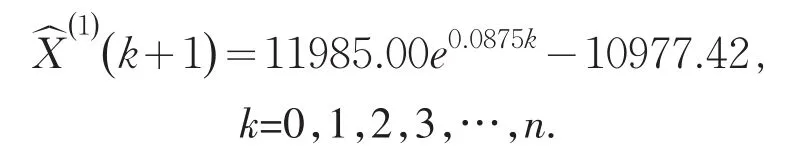
2.3 模型的检验

经过计算，得到表3数据.

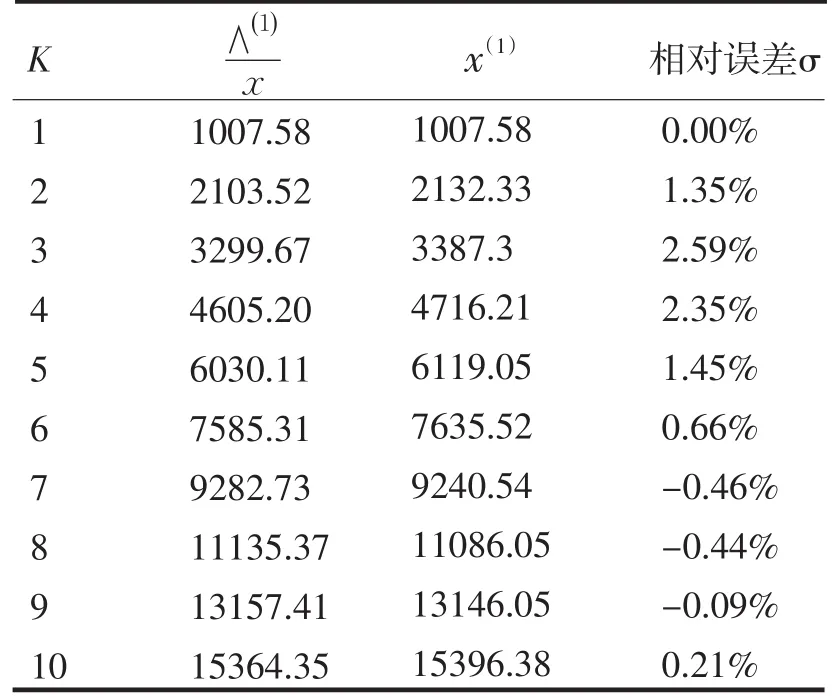
表3 模型预测检验与相对误差Tab.3 Forecast models testing and their differences

由上表可以看出，当K＞4时，相对误差几乎都小于1%，模型预测效果较好，而且预测时间周期越长，误差相对越小.

2.4 模型预测

用上述模型预测2010-2020年的结果：也就是取=11，12，13…19，21，由上述预测方程并通过还原得到表4数据.

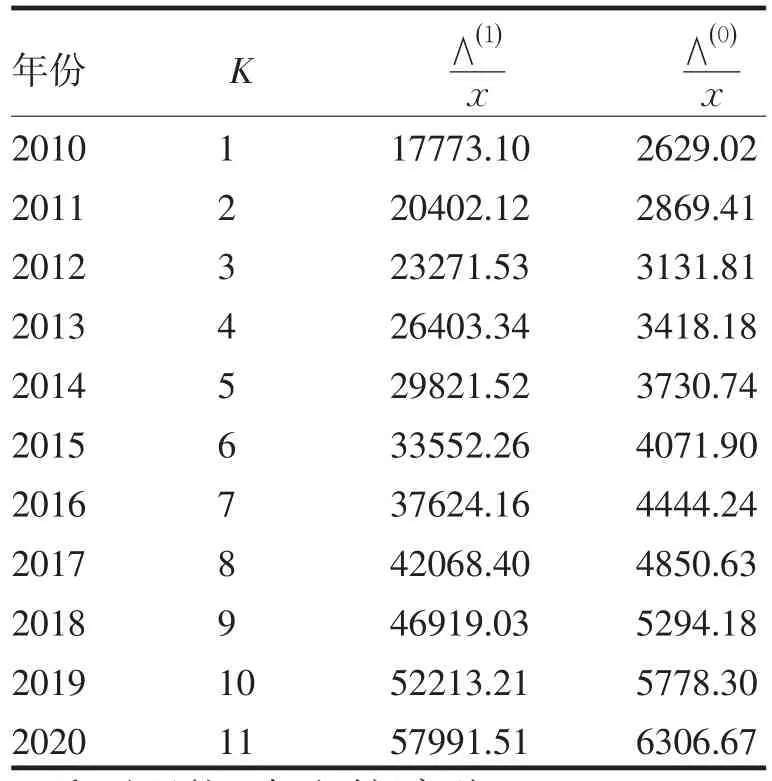
表4 海南省2010-2020年旅游接待人次数预测Tab.4 The visitor's reception amount forecasting during 2010-2020 in Hainan Province

从表4可以看出，本模型对海南省旅游接待人次数2010年的预测值为2629.02万人次，根据海南省旅游发展委员会的统计数据，截止到2010年12月底，海南省2010年旅游接待人次数为2587.34万人次，由此可见，本模型的预测效果相当不错，精度较高.

3 结论

对于旅游的相关研究而言，研究方法不是一成不变的，根据不同的理论系统建立模型，既要考虑到系统的属性，更要考虑进行研究的目的，这样才能使旅游相关研究有更强的指导意义.科学的旅游市场预测是制定旅游业相关政策和进行有效管理的重要依据，本文根据旅游业系统的属性，运用灰色系统理论来预测旅游接待人次数，是一种探索.根据本文的预测，到2020年，海南旅游接待人次数将达到6306.67万人次，与纲要中制定的7680万人次的目标还有不小的差距，当然，随着国际旅游岛建设的深入，海南旅游业的发展可能进入一个加速的阶段，本模型中虽然对这一因素考虑并不充分，但这一预测方法为旅游市场预测的继续研究和探索提供了进一步的思路.

[1]宁德煌.灰色系统GM(1,1)模型及其在市场预测中的应用[J].昆明理工大学学报,2005,25(3):111-115.

[2]闵惜琳.基于灰色预测模型GM(1，1)的人才需求分析[J].科技管理研究,2006(6):72-75.

[3]唐晓云,赵黎明,秦彬.灰色系统理论及其在旅游预测中的应用——以广西桂林为例[J].西安电子科技大学学报:社会科学版,2007,18(3):1-5.

[4]刘思峰,郭天榜,党耀国,等.灰色系统理论及其应用[M].北京:科学出版社,1999.

[5]郭齐胜.系统建模原理与方法[M].北京:国防科技大学出版社,2003.

[6]海南省统计局.海南统计年鉴[M].北京:中国统计出版社,2001-2010.

The Tourism Market Forecasting of Hainan Province——Research Based on Grey System Theory

HE Biao1，ZHU Lianxin2
（1.College of Hainan University，Haikou570228，China；2.College of Economics and Management，Hainan University，Haikou570228，China）

Scientific forecasting of tourism market is important for sustainable development of tourism.The grey system theory and GM（1，1）grey forecasting model are briefly analyzed in this paper,and combining with the characteristics of the tourism system,grey forecasting model GM（1，1）is applied to the regional tourism market forecasting.Finally,an ex⁃ample of Hainan Province is taken to illustrate the application of the model with satisfactory results obtained.

Grey system theory；GM（1，1）model；Hainan province；Tourism Market；Forecasting

F 590.8

A

1674-4942（2011）04-0458-04

2011-09-29

国家自然科学基金项目（71161008）

黄 澜