均匀直线式天线阵方向图分析

张福恒

（海南师范大学 物理与电子工程学院，海南 海口 571158）

均匀直线式天线阵方向图分析

张福恒

（海南师范大学 物理与电子工程学院，海南 海口 571158）

分析了常见文献中关于均匀直线式天线阵分析所存在的问题及不足.对均匀直线式天线阵空间方向图进行了详细分析，给出了数学分析计算公式.以实例介绍了如何分析均匀直线式天线阵立体空间方向图.文中的方法及结论也适用于由磁偶极子、短偶极子、半波或全波单元天线组成的均匀直线式天线阵.

单元天线；天线阵；方向因子；天线阵方向因子；方向图

天线的方向性是天线的一个重要特性.为了改善和控制天线的方向性，通常使用多个简单天线构成复合天线，即天线阵.适当设计各单元天线的类型、数目、电流幅值及相位、单元天线的取向及间隔，可得到所需的天线阵方向性.天线阵方向性原理可由最简单的均匀直线式天线阵说明.通常文献对于均匀直线式天线阵方向性分析侧重于天线阵阵因子的方向性分析，其方法如下[1-5]：

考虑n单元均匀直线式天线阵，各单元天线平行于z轴沿x轴均匀排列，每两单元天线之间相隔距离为d，见图1.场点的距离远大于天线阵的尺寸，因此每一个单元天线到场点的连线可看成是平行的，因此相邻两单元天线的波程差均可认为为Δr，Δr=dcosφ.φ为场点位置矢量r与天线阵轴线x轴的夹角.各单元天线中的电流相同，幅值均为I0，相位依次递减α，分析得出天线阵的方向因子为[2-3]：

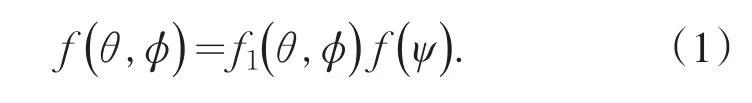
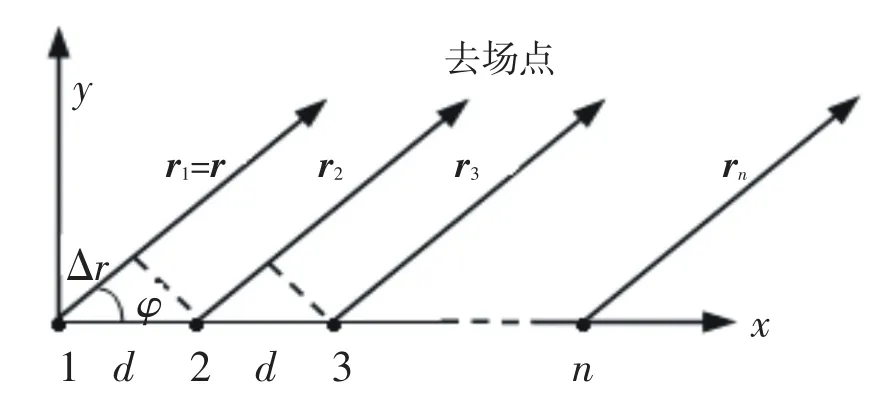
图1n单元均匀直线式天线阵Fig.1A n-element uniform linear antenna array

式中 f1(θ,φ)为单元天线的方向因子；

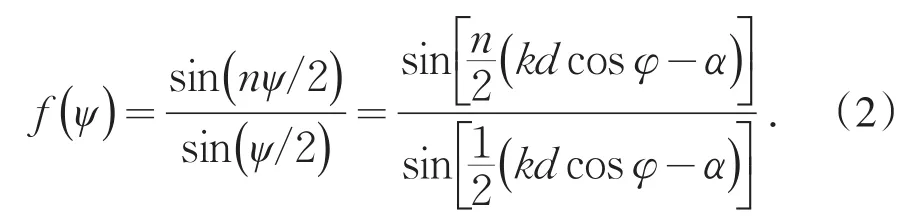
为天线阵阵因子，ψ=kdcosφ-α.

将（2）式对ψ求导，可得阵因子达到最大值的条件.即[1-5]

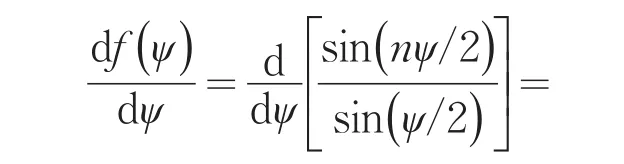
以上对n单元均匀直线式天线阵阵因子的分析存在一些问题：1）因天线方向图函数是天线方向因子的绝对值，求解（3）式从数学上来讲求出的是极大值，而不是最大值；2）（6）式的解并不是（5）式的全部解，它应该是ψ/2=±mπ,m=0，1，2，…，这样才符合（3）式的解.另外，对于等式的运算应避免等式两边同时乘或除以一个零值，以避免漏根或增根，文献[1-5]中的运算过程中没有考虑到这一点.例如当单元天线数n为奇数时，ψ/2=±mπ±π/2也是（3）式的解，而文献[1-5]中没有这一结论.（8）式中应有一个正负号；3）仅分析了均匀直线式天线阵阵因子的方向性问题，天线阵的方向性应和单元天线一起分析；4）天线的方向性在空间应是立体的，而上面的讨论并未涉及到.

针对以上问题，我们有必要对均匀直线式天线阵重新加以分析.下面我们将给出均匀直线式天线阵立体方向图的分析方法.

1 均匀直线式天线阵方向因子

注意到场点P（r）并不一定在xy平面上.在图2中，x轴即为均匀直线式天线阵轴线.由图2，易求得：

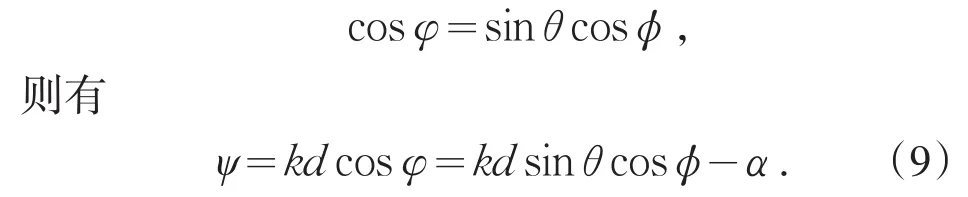
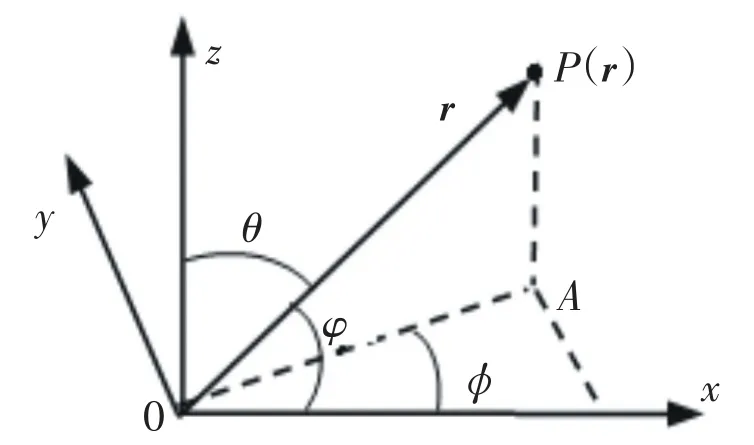
图2 φ,θ,φ关系图Fig.2 The relation among the anglesφ,θand φ

因此，天线阵阵因子（2）式可写成：

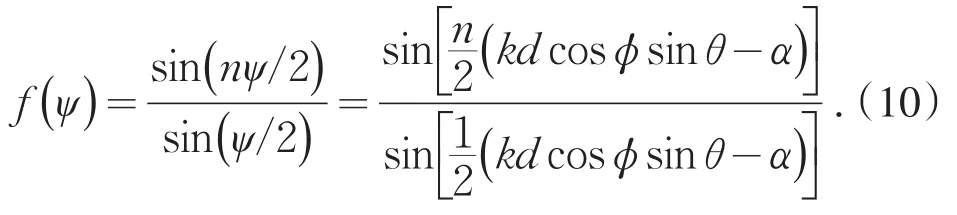
天线阵的方向因子仍为（1）式.由此我们看到，天线阵方向图与单元天线方向因子、单元天线数n、单元天线间间隔d、单元天线的递减相位差α以及方位角φ和θ有关.即（1）式给出了天线阵辐射方向空间立体图.

因（10）式中分子为 sin(n ψ/2) ，而分母为sin(n ψ/2) ，n＞1，因此（10）式在分母 sin(ψ /2)=0时有最大值.即 ψ=±2mπ 时有最大值，m=0，1，2，….利用罗必塔法则可求得（10）式最大值为n，可称为天线阵阵因子主极大值.

2 均匀直线式天线阵方向图分析

天线阵方向图由（1）式给出，结合（10）式，它在空间给出的是一个立体方向图.我们可分别在xy平面、yz平面上和xz平面上分析天线阵方向图.

为简单，我们考虑由赫兹单元天线组成的n单元赫兹均匀直线式天线阵.赫兹单元天线方向因子f1(θ ,φ )=sinθ[1-5].

1）在xy平面，θ=π/2,f1(θ ,φ )=sinθ=1，天线阵方向图决定于阵因子 f(ψ )，且仅是φ的函数.此时，天线阵方向因子为：

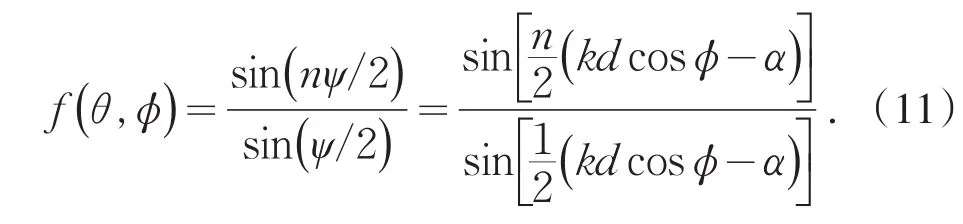
同前面分析，上式出现最大值条件为分母为零.即在xy平面最大值条件为：

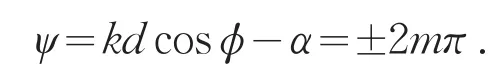
因此最大辐射方向满足：

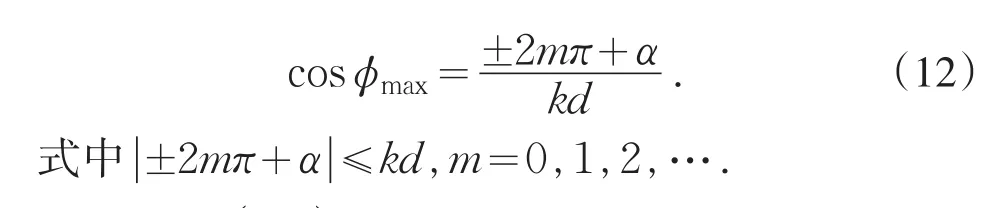
在sin(ψ/2)≠0，即非最大值的条件下，令（11）式为零可得场强为零的ψ值，此值对应的点为方向图零点，这些零点值涉及到单元天线数n、间隔d、递减相位差α等天线阵参数.令（11）式为零得：

任意两个相邻零点之间，场方向图有一个次极大点，且sin(nψ/2)≠0.因此两个相邻零点之间的次极大值点，可由（11）式中令分子sin(nψ/2)=1求出.因为是两相邻零点之间的次极大值，因此出现次极大满足：ψ=ψ0+β,β为小于两相邻零点值角度差的角度.因此有：

2）在yz平面，φ=π/2.由（10）式知，对于给定的相位差α，此时天线阵的方向图由 f1(θ ,φ )=sinθ来确定.即：

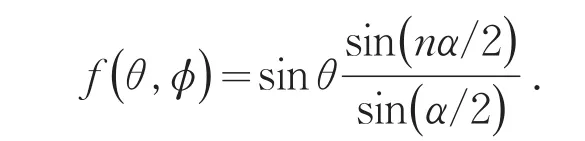
注意到方向图函数为上式的绝对值，因此辐射最大方向为±π/2；零点值在0和π.

要注意的是，若α=0，则由罗必塔法则可求得天线阵阵因子为n，即在这情况下yz平面方向图仍为以上结论.

3）在xz平面，φ=0，天线阵的方向图因子

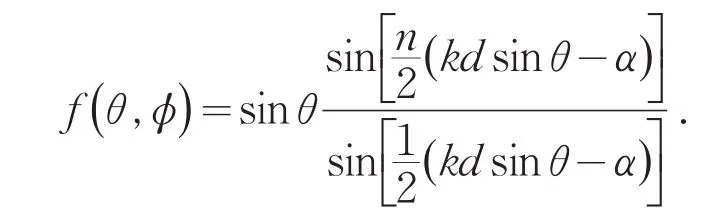
上式对于求解极大值较为困难，但我们可以求出其零点值.将（9）带入上式，可以判定零点值出现在sin(ψ/2)≠0处.因此根据上式，零点值可由单元天线方向因子sinθ=0和下式给出，

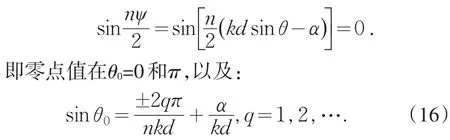
式中(± 2qπ/nkd+α/kd )≤1.两个相邻零点之间，场方向图有一个极大点，此极大点原则上可以通过求导数的方法求得.但由（16）式可看出，若n越大，零点越多.即在要求不严或n很大时，极大点可近似认为处于两零点的中间值.

由以上讨论，可知不同α值有不同的方向图，这就是相控阵雷达的原理.

因磁偶极子天线[1-3，5]、短偶极子天线[5]的方向因子和赫兹天线一样均为sinθ，因此以上的结论也适用于由磁偶极子、短偶极子单元组成的均匀直线式天线阵.

因对称天线方向因子为[2-3]：

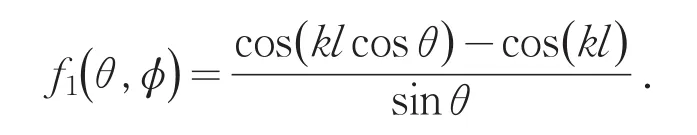
对于半波和全波单元天线，kl=π/2和π.

在xy平面，θ=π/2，半波和全波天线的方向因子为1和2.即半波天线组成的天线阵方向图和赫兹的一样，而全波天线组成的天线阵方向图和赫兹的相似.

在yz平面，φ=π/2.此时天线阵的方向图由单元天线方向因子 f1(θ ,φ)确定.由罗必塔法则可求得半波和全波天线在θ→0和π时，其为方向图零点解.对 f1(θ ,φ )求导后可判定只有在 θ=±π/2时有最大值.即和赫兹天线阵一样结论.

在xz平面，φ=0，由上讨论知 f1(θ ,φ )的零点值在0和π，也和赫兹天线阵结论一样.

由此得出，由半波或全波单元天线组成的均匀直线式天线阵在三个平面上与赫兹单元天线组成的均匀直线式天线阵有相同或相似的方向图.

3 例

虽然分析天线阵方向图用计算机作图工具比上面的数学分析更为方便，但一般的作图工具只能作定性的分析，有时不易得到确切值.因此，上面的讨论分析还是有意义的.

下面我们以阵元间距为λ/2、滞后相移α=π/4的4单元赫兹均匀直线式天线阵为例来说明.此时：

取上式绝对值，利用计算机画出xy平面方向图见图3.由图看出最大值、零点值及次极大值方向与计算结果符合.

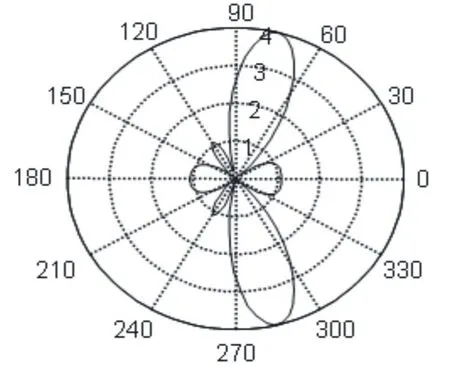
图3xy平面方向图Fig.3 Field pattern in the xy plan

2）yz平面方向图.

在yz平面，φ=π/2.由前面求得辐射最大方向为±π/2；零点值在0和π.天线阵因子

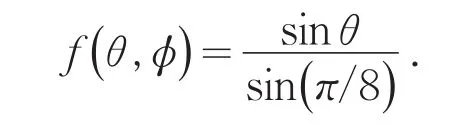
其给出的方向图见图4.最大值、零点值方向和计算结果符合.

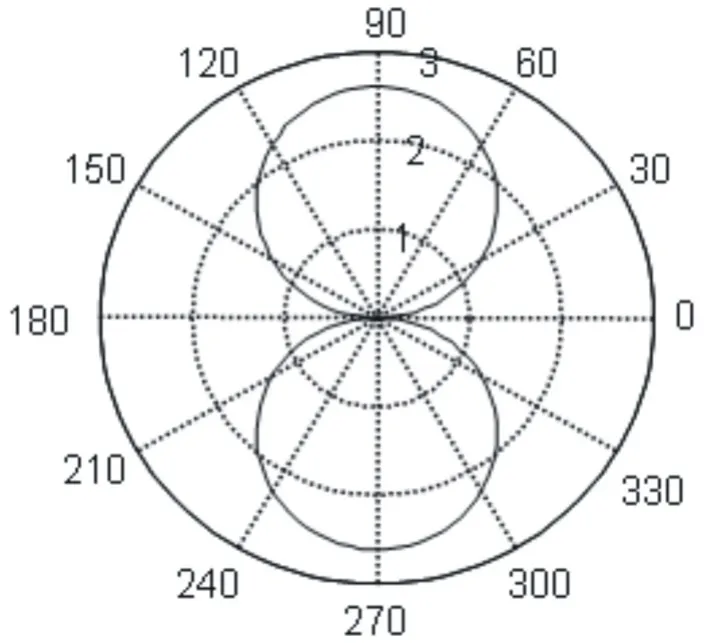
图4 yz平面方向图Fig.4 Field pattern in the yz plan

取上式绝对值，画出xz平面方向图见图5.零点值、极大值方向和计算结果符合.

根据（1）式，本例的天线阵空间方向图见图6.

以上讨论表明，对天线阵方向图的分析，采用计算机一般作图工具的方法更直观清晰，但数学分析的方法可得到精确数值.

4 结语

本文指出了常见文献中分析天线阵方向图存在的一些问题，给出了分析均匀直线式天线阵立体方向图的一般方法.

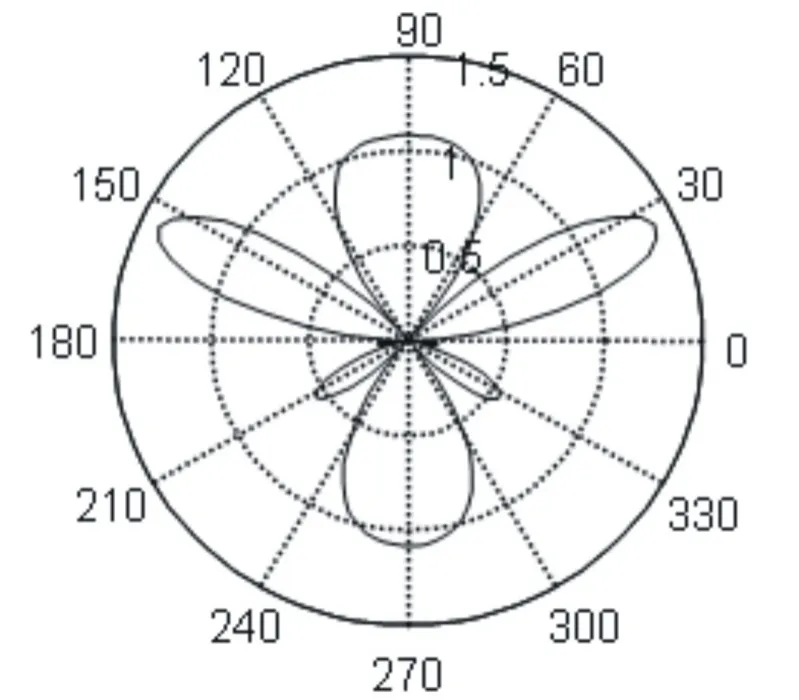
图5xz平面方向图Fig.5 Field pattern in the xz plan

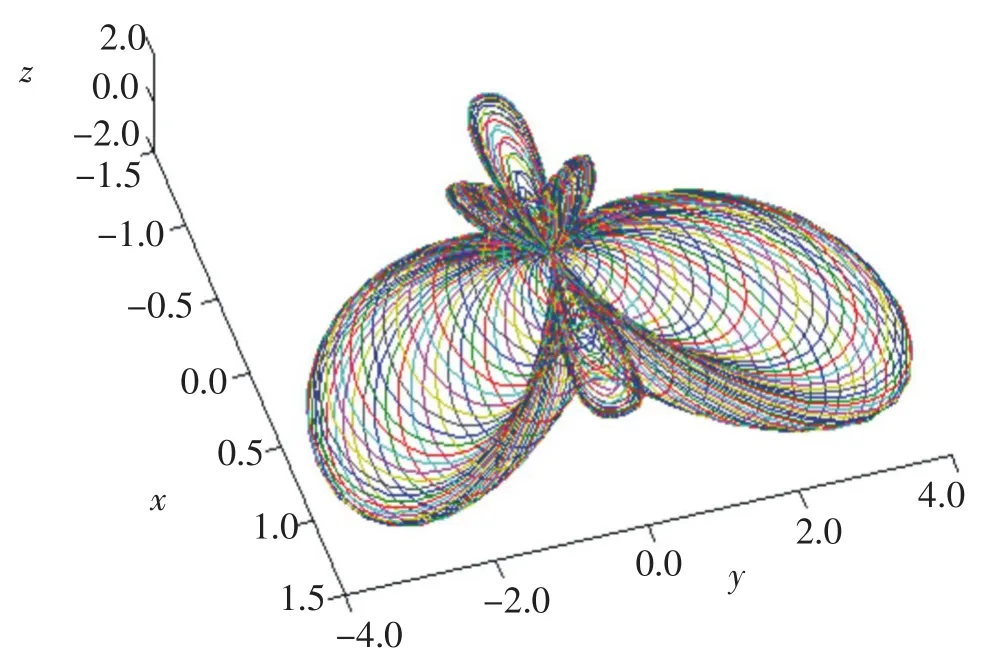
图6 空间方向图Fig.6 Spatial directivity pattern

一般国内文献仅分析了天线阵阵因子方向图问题[1-5]，也有国外文献[6]分析了xy和xz两个平面天线阵方向图的问题.我们分别讨论了天线阵在三个平面的辐射方向图问题，即使在依次递减相位差α=0时也可讨论天线阵在三个平面的辐射方向图问题.并借助计算机画出了天线阵三个平面上的方向图及空间方向图.本文讨论方法及结论也适用于由磁偶极子、短偶极子、半波或全波单元单元天线组成的均匀直线式天线阵.

本文中对xy平面方向图的分析，实际上就是均匀直线式天线阵阵因子方向图的分析.

[1]谢处方,饶克谨.电磁场与电磁波[M].3版.北京:高教出版社,1999:225-237．

[2]沈熙宁.电磁场与电磁波[M].北京:科学出版社,2006:423-447．

[3]杨儒贵.电磁场与电磁波[M].2版.北京:高教出版社,2007:295-309．

[4]冯林,杨显清,王园.电磁场与电磁波[M].北京:机械工业出版社,2004:215-217．

[5]王家礼,朱满座,路宏敏.电磁场与电磁波[M].西安:西安电子科技大学出版社,2000:223-226．

[6]Bhag Singh Guru Hüseyin R Hizroĝlu.Electromagnetic Field Theory Fundamentals(Second Edition)[M].北京:机械工业出版社,2005:552-575．

Analysis of Uniform Linear Antenna Array Directivity Patterns

ZHANG Fuheng
（College of Physical and Electrical Engineering，Hainan Normal University，Haikou571158，China）

This paper pointes out some problems and insufficiency existing in some familiar literatures relating to the directivity pattern analysis of the uniform linear antenna array.On the other hand,it analyzes in detail the spatial direc⁃tivity pattern of the uniform linear antenna array and gives the calculating formulas about antenna array spatial directivi⁃ty pattern.It introduces how to analyze mathematically three-dimensional directivity pattern of the uniform linear anten⁃na array with an example.The method and the conclusions in this paper are applicable for the uniform linear antenna ar⁃ray constructed by magnetic dipole antenna,short dipole antenna,half-wave dipole antenna or full-wave antenna.

elemental antenna；antenna array；directivity factor；directivity factor of antenna array；directivity pattern

TN 820.1+2

A

1674-4942（2011）04-0403-05

2011-10-15

黄 澜