参数随时间变化的任选期权的定价公式
王海叶
(宁德师范学院 数学系,福建 宁德 352100)
参数随时间变化的任选期权的定价公式
王海叶
(宁德师范学院 数学系,福建 宁德 352100)
基于股票价格服从对数正态分布的假设,利用风险中性定价原理,对标准股票欧式任选期权进行推广,得到参数随时间变化的股票欧式任选期权在任意时刻t的定价公式.
股价;对数正态分布;风险中性定价原理;随机微分方程
20世纪70年代初,Fischer Black 和Myron Scholes在欧式期权定价方面取得了重大突破,推导出标准欧式看涨期权和看跌期权的价值. 近年来,国际金融市场除了交易人么广为熟悉的欧式、美式等标准期权之外,还涌现出了大量由标准期权变化、组合、派生出的新品种,称之为新型期权,新型期权是比标准欧式或美式看涨期权和看跌期权盈亏状态更为复杂的衍生证券. 任选期权就是一种新型期权,有时也称为选择期权[1],具有如下特征:经过一段指定时期T后,持有人能选择期权,或者是看涨期权或者是看跌期权. Rubinstein应用标准看涨期权和看跌期权的Black-Scholes定价公式,推导了标准任选期权在当前时刻的价值. 然而, 在金融市场中,利率和波动率随时间变化,本文基于标的资产的对数正态分布假设,应用风险中性定价原理,推导了参数随时间变化的股票欧式任选期权在任意时刻t的定价公式.
1 模型描述
1)假设考虑的任选期权做出选择的时刻为T,基于的看涨期权的执行价格为K1,到期日为T1≥T;看跌期权的执行价格为K2,到期日为T2≥T.
2)没有交易费用或税收;所有证券都是高度可分的;
3)在期权到期之前,股票无红利支付;
4)股票交易是连续进行的,且无卖空限制;
5)无风险利率r,股票期望收益率μ和股价波动率σ随时间变化;
6)不存在无风险套利机会;
2 参数随时间变化的欧式任选期权的定价公式
引理1[3]在时间依赖参数的金融市场中,期权的无套利价值为

引理2[2]1)已知看涨期权的执行价格K1,到期日T1≥T,看跌期权的执行价格K2,到期日T2≥T,则存在唯一确定的S*>0,使得

定理3 当股票价格的利率、波动率随时间变化时,任选期权在任意时刻t∈[0,T]的定价公式为:
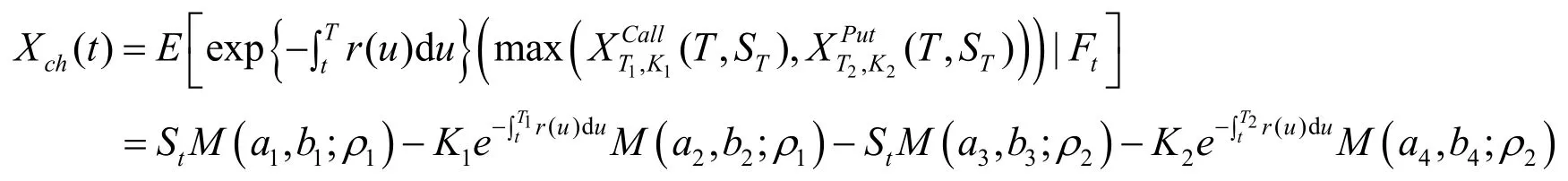
这里 M( x, y;ρ)是有相关系数ρ的标准二维正态分布函数,N是标准累积正态分布,并且

证明:假设股票价格的变化用下面的随机微分方程表示:

其中zt遵循维纳过程.
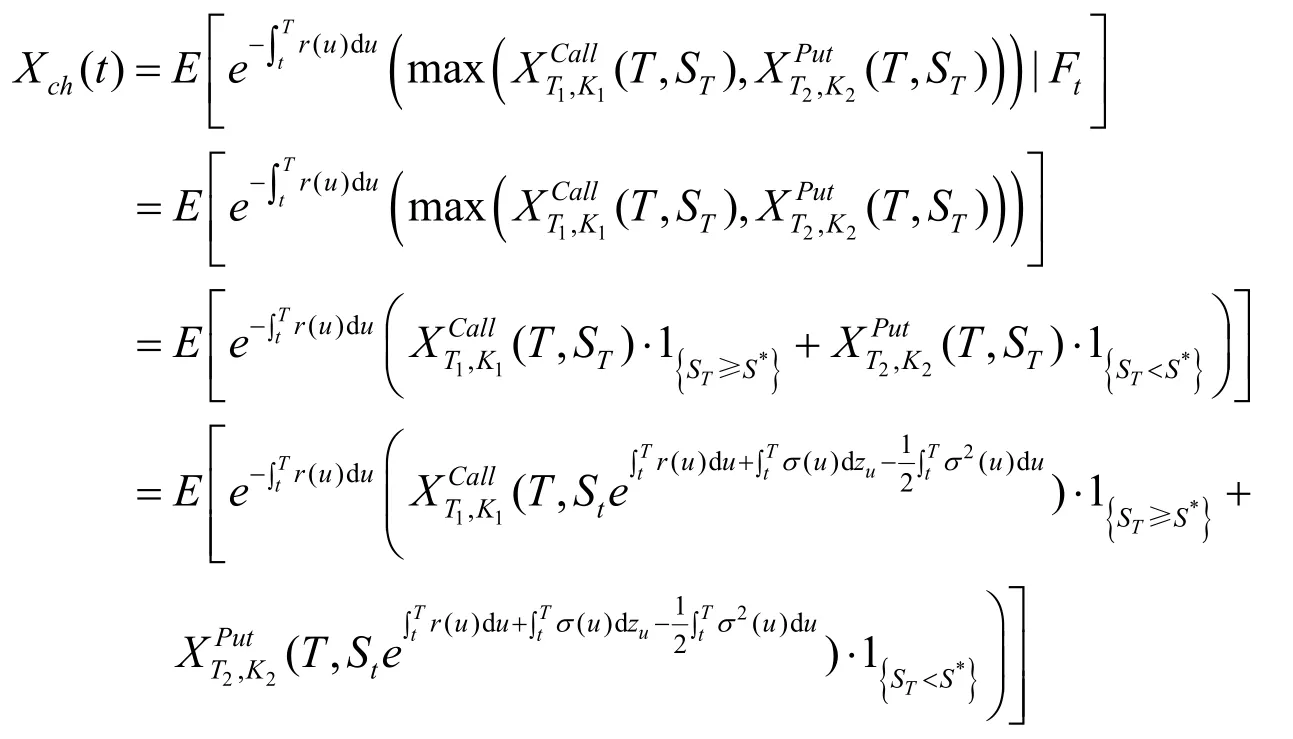

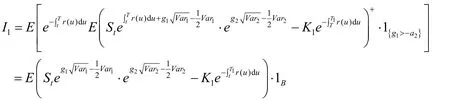
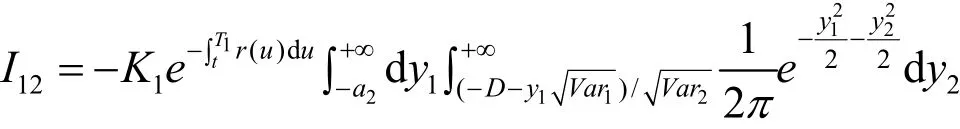

类似地可得

结合(2)、(3)有

类似地可得
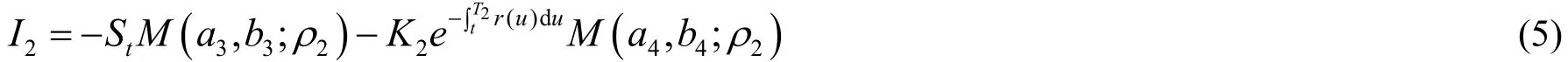
结合(4)、(5)可得利率和波动率随时间变化的任选期权在任意时刻t的定价公式为:

3 结论
在金融市场中,利率和波动率随时间变化,基于股票价格服从对数正态分布的假设,利用风险中性定价原理,得到了参数随时间变化的股票欧式任选期权在任意时刻t的定价公式,对标准股票欧式任选期权进行了推广.
[1] HULL JOHN C. 期权、期货、和其他衍生产品[M]. 张陶伟, 译. 3版. 北京: 华夏出版社, 2000.
[2] KORN RALF, KORN ELKE. Option Pricing and Portfolio Optimization[M]. [S. l.]: American Mathematical Society, 2000.
[3] 李荣华, 戴永红, 常 秦. Compound Options with Time dependent Parameters[J]. Chinese Journal of Engineering Mathematics, 2005, 22(4): 692-696.
(责任编辑:饶 超)
Pricing Formula of Chooser Option with Time-Dependent Parameters
WANG Hai-ye
(School of Mathematics, Ningde Normal University, Ningde 352100, China)
Based on assumptions of stock price’s lognormal distribution, the standard european chooser options of stocks is extended using risk-neutral pricing principle and the pricing formula of european chooser options of stocks is derived in any time t .
Stock price; Lognormal distribution; Risk-neutral pricing principle; Stochastic differential equation
O22
A
1009-2854(2011)05-0005-03
2011-04-25
王海叶(1981— ),女,山西朔州人, 宁德师范学院数学系讲师.

