饱和层状场地中任意凹陷地形对入射SV波的散射

尤红兵 梁建文 赵凤新

1）中国北京100029中国地震灾害防御中心

2）中国天津300072天津大学土木工程系

饱和层状场地中任意凹陷地形对入射SV波的散射

尤红兵1），梁建文2）赵凤新1）

1）中国北京100029中国地震灾害防御中心

2）中国天津300072天津大学土木工程系

利用饱和土层的精确动力刚度矩阵和动力格林（Green）函数，采用间接边界元法，在频域内求解了层状饱和场地中任意凹陷地形对入射SV波的散射问题.通过自由场反应分析，求得凹陷地形表面各点的位移和各单元的应力响应；同样计算了虚拟分布荷载的格林影响函数，求得相应的位移和应力响应；根据边界条件确定虚拟分布荷载，将自由场位移响应和虚拟分布荷载产生的响应叠加得到了问题的解答.本文方法可进行退化，所得结果与不含孔隙水的干土结果一致.对3种饱和场地自由场反应和凹陷地形对入射SV波散射进行分析，并与相应干土结果进行了对比.研究表明，入射角度、入射频率、粘性耦合系数等对地表位移有重要影响.在饱和场地中，入射波频率和粘性耦合系数（土的渗透性）影响土层中波的传播速度，导致地表位移幅值与干土场地产生明显差异，尤其是入射角在30°—60°范围内.因此，在饱和场地动力分析中应综合考虑入射角度和入射频率对场地地表位移的影响.

饱和层状半空间 任意凹陷地形 SV波 散射

引言

地震波在层状弹性介质中的传播，一直是众多学者所关注的课题之一.Biot（1962）建立了饱和孔隙介质的动力方程，为研究饱和孔隙介质的波动问题奠定了理论基础.Rajapakse和Senjuntichai（1995）、Pan（1999）、尤红兵（2005）及尤红兵等（2008）分别给出了饱和土层和半空间的精确动力刚度矩阵，解决了水平层状场地中波的传播问题.Senjuntichai和Rajapakse（1994）、杨峻等（1997）、尤红兵和梁建文（2005）采用不同方法，研究了饱和层状场地中的动力格林（Green）函数.Liang和You（2004，2005）将 Wolf土－结构动力相互作用理论（Wolf，1985；Vogtetal，1988）推广到了饱和层状场地，解决了计算层状饱和场地中局部地形对弹性波散射的关键问题.并采用间接边界元法在频域内求解了层状饱和场地中任意凹陷地形对入射P波的散射问题（尤红兵等，2008）.李伟华和赵成刚（2004）及Li和Zhao（2005）、巴振宁（2005）等研究了均匀饱和半空间中局部地形对平面SV波的散射，但对于层状饱和场地中任意凹陷地形对入射SV波散射的研究少见报道.

本文利用饱和土层的精确动力刚度矩阵，给出了饱和层状场地动力格林函数的求解方法.采用间接边界元法，在频域内求解了层状饱和场地中任意凹陷地形对入射SV波的散射问题.通过算例，研究了入射角度、入射频率、粘性耦合系数等不同参数对地表位移的影响，并与相应干土结果进行对比.

1 基本方法

饱和层状场地中任意凹陷地形如图1所示.对入射SV波的散射可通过自由场、动力格林函数的计算，根据不同的边界条件，求解得到入射SV波的散射.图1中，S为任意凹陷地形的边界；均布荷载幅值p（s），r（s），q（s）分别为计算动力格林函数所施加的虚拟水平、竖向荷载及孔压；Ux（s）和Uz（s）分别表示沿线S各点产生的土骨架水平和竖向位移；w（s）为沿线S流体相对于土骨架的法向位移；tx（s）和tz（s）分别表示沿线S各单元产生的水平和竖向应力；tp（s）为孔压；γ为SV波入射角.

1.1 自由场计算

进行自由场分析时，假定无凹陷地形存在.根据土层各表面透水和不透水边界条件及位移、应力和孔压在交界面上的连续条件，利用饱和土层和半空间的精确动力刚度矩阵（尤红兵，2005；Liang，You，2004），采用直接刚度法可求得入射SV波的饱和水平层状场地的自由场响应，进而得到假想边界S上各点的位移和各单元的应力响应.

自由场的动力平衡方程为

图1层状场地示意图Fig.1 Discretization of the canyon surface

式中，［SP1－P2－SV］为整体动力刚度矩阵，由各土层和半空间的刚度矩阵组成；Ux1，Uz1，wz1，Uxn＋1，Uzn＋1，wzn＋1分别表示各土层土骨架水平和竖向位移及流体相对于土骨架的法向位移；Rxo，Rzo和Pzo是底部荷载向量幅值分量；i为虚数单位.

通过求解式（1），最终得到沿边界S上各点自由场的位移［Uxf（s）Uzf（s）wf（s）］T和沿边界S上各单元应力［txf（s）tzf（s）tpf（s）］T.下标f表示自由场，其它符号意义同前.

1.2 动力格林函数计算

动力格林函数是在自由场（无凹陷地形）内部作用一单位荷载时，自由场任意一点的位移及应力响应.

当图1所示均布荷载幅值p（s），r（s）和q（s）作用在饱和层状场地中某一土层时的动力格林函数，可采用叠加原理得到.首先假定将作用荷载土层的顶面和底面固定.通过求解Biot动力方程，得到满足这样条件的相应反力，包括土层顶面和底面的应力和孔压，这个分析仅在作用荷载的土层上进行.然后，将得到的反力以相反的方向作用到由所有土层和半空间组成的总体系上.利用饱和土层和半空间的精确动力刚度矩阵，采用直接刚度法求得此时总体系的反应.最后，将上述两部分结果叠加，得到所求的动力格林函数.限于篇幅，详细计算公式可参见相关文献（尤红兵，2005；Liang，You，2005）.

边界透水的动力格林函数可表示为

边界不透水的动力格林函数可表示为

式中，［gu（s）］和［guu（s）］分别表示边界透水、不透水时的位移格林函数；［gt（s）］和［gtu（s）］分别表示边界透水、不透水时的应力格林函数；下标g仅表示作用均布荷载时得到的位移或应力，与f对应，区别于自由场；其它符号意义同前.

1.3 边界条件

当凹陷地形边界透水时，表面的应力和孔压为0，其边界条件可表示为

［W（s）］为权函数，一般取为单位矩阵.将式（3）代入式（6）得

其中，［Tp］＝∫s［W（s）］［gt（s）］ds；［Tf］＝－∫s［W（s）］［txf（s）tzf（s）tpf（s）］Tds.

通过求解式（7），得到均布荷载幅值；再代入式（2），叠加自由场结果，得到总的位移响应.

不透水边界时，w（s）＝0，边界条件为

利用式（5）得到

其中，［Tpu］＝∫s［W（s）］［gtu（s）］ds；［Tf］同前.

通过求解式（10），得到均布荷载幅值［p（s）r（s）q（s）］T；再代入式（4），叠加自由场结果，得到总的位移响应

图2 凹陷地形断面示意图Fig.2 Cross section of the canyon

2 方法验证

如果取水的质量密度为0，可将本文方法退化，所得结果与不含孔隙水的干土结果一致.Vogt等（1988）假定土层为理想弹性土（干土），给出了任意凹陷地形对SV波的散射，利用其中的算例来验证本文方法.

凹陷地形断面示意图如图2所示，土1和土2参数相同.梯形凹陷的底宽为L2；顶宽为L＝2L1＋L2，且L2＝2L1.半空间上覆土层的总厚度为H＝H1＋H2＝L1tan30°.土层和半空间的密度与泊松比相同；剪切波速比为1∶2；阻尼比分别为0.05和0.02.入射SV波的波长为λs1/L＝0.25，幅值为｜ASV｜＝0.5.根据图3结果所示，可以看出本文方法结果是可靠的，有较高的精度.图3中x/L为图2中凹陷地形表面各点的横坐标与梯形凹陷顶宽的比值；纵坐标分别为无量纲水平位移｜Ux｜/｜ASV｜和竖向位移｜Uz｜/｜ASV｜.｜Ux｜和｜Uz｜分别为地表各点水平、竖向位移幅值.

图3 与Vogt等（1988）相应结果比较Fig.3 Results compared with those of Vogt etal（1988）

3 算例分析

场地几何条件如图2所示.凹陷地形断面参数取L＝2L1＋L2，且L2＝2L1；土层厚度取为H＝0.5L1.饱和土参数如表1所示.根据粘性耦合系数b的不同，定义了3种渗透性不同的场地（场地A、场地B和场地C）.当b越大，土的渗透系数越小.假定界面透水.表中μ和λ是土骨架的两个Lamé常数；α和M为表征土颗粒和孔隙流体压缩性的常数；ρs和ρf表示土和水的质量密度，n为孔隙率.定义无量纲频率为ω为入射SV波的圆频率.为方便比较饱和场地和不含孔隙水的干土场地对SV波散射的差异，算例中干土场地参数取相应饱和土的固相参数.

表1 饱和场地计算参数Table 1 Parameters of the saturated site

3.1 自由场分析

首先分析入射SV时，4种不同场地（场地A，B，C及干土场地）自由场（无凹陷地形）地表位移的变化.图4为自由场地表位移幅值随入射频率的变化曲线.图5给出了自由场（以场地C和干土场地为例）地表位移幅值随入射角的变化曲线.图中，｜ASV｜为入射SV波的幅值，｜Ux｜为地表各点水平位移幅值，｜Uz｜为地表各点竖向位移幅值.

从图4中可以看出，当SV波垂直入射（γ＝90°）时，4种场地的水平位移幅值基本一致.其中干土场地与场地A的结果基本重合，场地B和C的结果略小.这是因为在计算中假定流体不承受水平剪应力，因而水平位移幅值基本一致；场地B和C的结果略小，是因为入射频率和粘性耦合系数对波速的改变，而干土场地中波速不变.竖向位移相等，全部为0.当入射频率接近场地的基频时，位移被明显放大.

图4 自由场地表位移幅值随无量纲入射频率的变化Fig.4 Surface displacement amplitude of free－field response versus dimensionless incident frequency

当SV波斜入射时，入射频率对场地地表位移有重要影响，并且饱和场地（场地A，B，C）自由场反应与相应干土场地自由场结果有明显不同.当入射角γ＝5°和30°时，随入射频率的增大，干土场地的水平位移幅值明显大于饱和场地结果，尤其是η＞3.0.而场地A的竖向位移幅值最大，在η＝2.56、γ＝30°时，最大竖向位移幅值达到2.586.入射角时γ＝60°时，当η≤2.0，饱和场地的水平位移均大于相应干土场地结果，其中场地C的结果最大.如当η＝1.136时，场地C的水平位移最大幅值为3.996，而相应干土结果仅为2.232，相差1.8倍.饱和场地的竖向位移幅值则明显小于相应干土场地结果，场地C的竖向位移幅值最小.当η＝3.408时，干土场地竖向位移幅值为1.721，而场地C的结果仅为0.512，相差3.36倍.

从图5中可看出，入射SV波时，入射角对饱和场地地表位移的影响规律与干土场地类似.入射角度和入射频率对场地地表位移均有重要影响，最大水平位移幅值不一定出现在SV波垂直入射情况下.如η＝1.0时，饱和场地和干土场地的最大水平位移幅值分别为4.18（场地C，γ＝57.6°）、5.66（干土，γ＝53.2°），远大于SV波垂直入射时的结果2.95（场地C）、2.79（干土）.但在饱和场地中，入射波频率会影响波的传播速度，导致地表位移幅值与干土场地产生明显差异，尤其是入射角在30°—60°范围内.因此，在饱和场地动力分析中应综合考虑入射角度和入射频率对场地地表位移的影响.

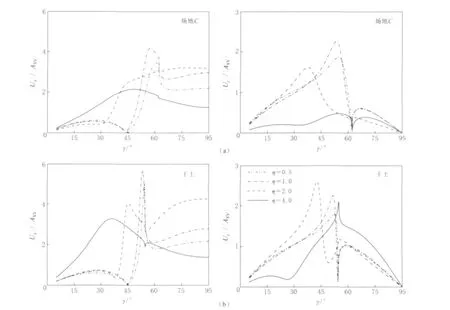
图5 自由场地表位移幅值随入射角的变化.（a）饱和场地；（b）干土场地Fig.5 Surface displacement amplitudes of free－field response versus SV wave incident angles.（a）For saturated site；（b）For dry site

3.2 凹陷地形的散射

图6和图7分别给出了入射SV波时，4种不同凹陷场地（场地A，B，C及干土场地）地表水平、竖向位移幅值比较.无量纲频率分别取1.0，2.0和4.0.

从图6和图7中可以看出，凹陷地形对地表位移幅值空间分布的影响随入射频率的增大而增大；频率越低，位移幅值越接近于自由场反应.3种饱和场地及干土场地中凹陷地形对SV的散射有明显不同.

在入射频率η＝1.0时，除入射角γ＝60°外，4种场地的地表水平、竖向位移幅值相差较小.当入射角为γ＝60°时，4种场地地表水平位移幅值相差较大.在x/L＝－0.5，即图2中x1点处，水平位移幅值分别为3.924（场地A）、4.212（场地B）、4.711（场地C）和2.497（干土）；而干土场地的竖向位移幅值明显大于饱和场地结果.当η＝2.0时，入射角分别为30°和90°时，4种场地地表水平位移幅值相差较大，而其它位移幅值相差较小.在x/L＝1.0处，水平位移幅值分别为1.497（场地A）、1.199（场地B）、0.957（场地C）和1.491（干土）.当入射频率较高（如η＝4.0）时，入射角分别为γ＝5°和30°时，干土场地地表水平位移幅值大于相应饱和场地结果，而3种饱和场地位移结果基本一致，相差较小.在3种饱和场地中，场地A中b＝0，土的渗透性最好，波传播中能量消耗减少，波速较高，地表位移幅值最大；场地C的渗透性最差，波速较低，地表位移幅值最小.这些差别说明入射角、入射频率、粘性耦合系数b（土的渗透性）等对位移结果有重要影响.

图8还给出了凹陷地形两边角和底部中点（图2中x1，x2，x3点，即x/L＝－0.5，0，0.5）处地表位移随入射角的变化曲线.

图6 四种不同凹陷场地地表位移幅值比较.（a）η＝1.0；（b）η＝2.0Fig.6 Comparison of the surface displacement amplitudes of four different sites（a）η＝1.0；（b）η＝2.0

图7 四种不同凹陷场地地表位移幅值比较（η＝4.0）Fig.7 Comparison of the surface displacement amplitudes of four different sites（η＝4.0）

从图8中可以看出，入射角度、入射频率以及水平位置对场地地表位移反应有重要影响.当SV波中入射频率较低（η＝1.0，2.0）时，入射角在45°—60°范围内地表位移变化较激烈；当入射频率较高（η＝4.0）时，入射角在30°—60°范围内地表位移变化较大.如η＝1.0时，干土场地中x1，x2和x3三点的最大水平位移幅值分别为6.78（γ＝53.2°），4.29（γ＝53.2°）和5.06（γ＝53.2°）.饱和场地（场地C）中x1，x2和x3三点的最大水平位移幅值分别为5.02（γ＝57.4°），2.90（γ＝56.6°）和3.55（γ＝57.8°）.由于场地土层对入射波的放大作用和凹陷地形对波的散射，x1点的水平位移幅值最大，x3点次之，x2点的水平位移幅值最小.

4 讨论与结论

利用饱和土层的精确动力刚度矩阵和动力格林函数，采用间接边界元法，在频域内求解了层状饱和场地中任意凹陷地形对入射SV波的散射问题.通过自由场反应分析，求得凹陷地形表面各点的位移和各单元的应力响应；同样计算了虚拟分布荷载的格林影响函数，求得相应的位移和应力响应；根据边界条件确定虚拟分布荷载，最终得到问题的解答.本文方法可进行退化，所得结果与不含孔隙水的干土结果一致.通过4种场地自由场反应和凹陷地形对入射SV波散射的算例分析，研究了入射角、入射频率、粘性耦合系数b（土的渗透性）等对地表位移的影响，结果表明：

1）入射角度和入射频率对饱和场地和干土场地的地表位移均有重要影响.斜入射与垂直入射的地表位移比值最大可达2倍以上，入射角在30°—60°范围内地表位移变化较大.应合理考虑入射角度及入射频率对场地地表位移的影响.

图8 x/L＝－0.5，0和0.5处地表位移幅值随入射角的变化Fig.8 Surface displacement amplitudes versus SV wave incident angles at the point x/L＝－0.5，0，0.5

2）在饱和场地中，入射频率和粘性耦合系数（土的渗透性）影响土层中波的传播速度，进而对饱和场地的动力响应影响较大.这是与干土场地反应明显不同的主要原因.

3）饱和场地结果与相应干土场地结果明显不同，应合理考虑孔隙流体的影响.

限于篇幅，本文仅考虑了凹陷地形表面透水情况，对于界面不同透水条件对位移结果的影响，以及饱和层状场地中其它任意形状洞室对入射弹性的散射，将另文讨论.

巴振宁.2005.饱和半空间中凹陷地形和隧洞对平面P、SV波的散射［D］.天津：天津大学：33－－62.

李伟华，赵成刚.2004.饱和土沉积谷场地对平面SV波的散射问题的解析解［J］.地球物理学报，47（5）：911－－919.

杨峻，吴世明，陈云敏.1997.弹性层和饱和半空间体系稳定动力响应［J］.土木工程学报，30（3）：39－－48.

尤红兵.2005.层状饱和半空间中凹陷地形或隧洞对弹性波的散射［D］.天津：天津大学：37－－50.

尤红兵，梁建文.2005.层状饱和场地中线性分布斜线荷载的动力Green函数［J］.振动工程学报，18（3）：335－－341.

尤红兵，梁建文，赵凤新.2008.层状饱和场地中任意凹陷地形对入射P波的散射［J］.岩土工程学报，30（6）：840－－849.

Biot M A.1962.Mechanics of deformation and acoustic propagation in porous media［J］.JApplPhys，33：1482－－1498.

Li W H，Zhao C G.2005.Scattering of plane SV waves by cylindrical canyons in saturated porous medium［J］.SoilDynamEarthqEng，25（12）：981－－995.

Liang J W，You H B.2004.Dynamic stiffness matrix of a poroelastic mutli－layered site and its Green’s functions［J］.EarthquakeEngineeringandEngineeringVibration，3（2）：273－－282.

Liang J W，You H B.2005.Green’s functions for uniformly distributed loads acting on an inclined line in a poroelastic layered site［J］.EarthquakeEngineeringandEngineeringVibration，4（2）：233－－241.

Pan E.1999.Green’s functions in layered poroelastic half－space［J］.IntJNumAnalMethGeomech，23（13）：1631－－1653.

Rajapakse R K N D，Senjuntichai T.1995.Dynamic response of a multi－layered poroelastic medium［J］.EarthqEng StructDynam，24（5）：703－－722.

Senjuntichai T，Rajapakse R K N D.1994.Dynamic Green’s functions of homogeneous poroelastic half plane［J］.JEng MechASCE，120（11）：2381－－2404.

Vogt R F，Wolf J P，Bachmann H.1988.Wave scattering by a canyon of arbitrary shape in a layered half space［J］.EarthqEngStructDynam，16（6）：803－－812.

Wolf J P.1985.DynamicSoil-StructureInteraction［M］.Englewood Cliffs：Prentice－Hall：112－－142.

尤红兵 中国地震灾害防御中心副研究员，一级注册地震安评师.2005年天津大学结构工程专业毕业，获博士学位.主要从事结构抗震，复杂介质中地震波传播理论，电气设备减隔震技术等相关领域的研究.

SV wave scattering by a canyon of arbitrary shape in a saturated layered half－space

You Hongbing1），Liang Jianwen2）Zhao Fengxin1）
1）ChinaEarthquakeDisasterPreventionCenter，Beijing100029，China
2）DepartmentofCivilEngineering，TianjinUniversity，Tianjin300072，China

Based on exact dynamic－stiffness matrices and Green’s functions of a layered saturated soil，the scattering of SV waves by a canyon of arbitrary shape in a saturated layered half－space is modeled using the indirect boundary element method in frequency domain.The free－field responses are calculated to determine the displacement and stress at canyon surface，and fictitious distributed loads are then applied on the canyon surface in the free field to calculate the Green’s functions for displacement and stress.The amplitude of the fictitious distributed loads are determined from the boundary conditions，and the dis－placements arising from the waves in the free field and from the fictitious distributed loads are summed to obtain the solution.The present method can be degenerated and the result agrees well with that of dry soil without fluid.The free－field responses of three different saturated sites are calculated and numerical results for displacements of the canyon due to incident SV waves are presented.The results of the saturated sites are compared with that of corresponding dry layered site.It is shown that the incident angle，the frequency of incident wave and penetrability of soils have a great effect on displacements.The frequency of incident wave and the internal friction parameter or the penetrability of soil influence the velocities of three waves propagated in layered saturated soils，which result in the apparent difference between the saturated layered halfspace and the dry site，especially for the incident angles from 30°to 60°.The incident angle and frequency of incident wave should be comprehensively considered in dynamic analysis of the saturated sites.

saturated layered half－space；canyon of arbitrary shape；SV wave；scattering

10.3969/j.issn.0253－3782.2011.06.004

TU433

A

尤红兵，梁建文，赵凤新.2011.饱和层状场地中任意凹陷地形对入射SV波的散射.地震学报，33（6）：735－－745.

You Hongbing，Liang Jianwen，Zhao Fengxin.2011.SV wave scattering by a canyon of arbitrary shape in a saturated layered half－space.ActaSeismologicaSinica，33（6）：735－－745.

国家自然科学基金（50978183）和地震行业科研专项（200708034）共同资助.

2011－01－06收到初稿，2011－04－13决定采用修改稿.

e－mail：hbyou＠126.com