拟-逆半群上的群同余和最小群同余
焦红英,刘卫江
(空军工程大学 理学院,陕西 西安 710051)
拟-逆半群上的群同余和最小群同余
焦红英,刘卫江
(空军工程大学 理学院,陕西 西安 710051)
利用拟-逆半群的满的、自共轭的子半群,定义了拟—逆半群上的群同余,并给出了该类半群上的最小群同余的刻画.
拟-逆半群;群同余;最小群同余;自共轭
1 引言及准备知识
上世纪七十年代末开始,为人们所关注的所谓拟正则(或称幂正则,π-正则)半群是目前非正则半群研究中的一个活跃的领域.J.L.Galbiati和M.L.veronesi在《On quasi-completely regular semigroups》中最先讨论拟正则半群,并刻画了拟正则半群的基本性质和特征.对于拟—逆半群已有很多学者做过研究[1-4].1997年,田振际在文[5]中研究了拟—逆半群的拟—逆子半群格的直积分解,并且刻画了拟—逆子半群格的模格的拟—逆半群的性质及特征;2001年,他还证明了拟—逆半群的同态像也是拟—逆半群,同时给出了拟—逆半群上的最小拟群同余的构造.
文中未给出的术语和记号见文献[6].


引理1[7]令S为拟-逆半群,则有
(i)若 a∈Reg(S )⋂ ES,则a∈ES;
(ii)若e,f,ef,fe∈ES则ef=fe.
引理2[7]令S为拟正则半群,则下列各款等价:
(i)半群S是拟-逆半群;
(ii)半群S的每个L-类和每个R-类最多包含一个幂等元;
(iii)ES是诣零半群的半格;
(iv)关于任意的 e1,e2,…,em∈ES存在 n∈N ,使得
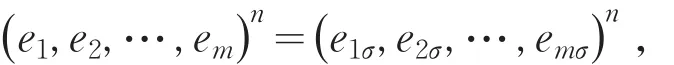

2 主要结果及证明

下面我们给出拟-逆半群上的群同余以及最小群同余.
定理1令半群S是拟-逆半群,H是S的满幂自共轭拟正则子半群,则




[1]田振际.π-逆子半群格是模格的π-逆半群[J].系统科学与数学,1997,17(3):226-231.
[2]宫春梅,任学明.严格π-正则半群上的最小群同余[J].西安建筑科技大学学报:自然科学版,2005,37(1):146-148.
[3]彭少玉,郭洪霞,刘红霞.左(右)强π-逆半群的最小群同余[J].烟台师范学院学报:自然科学版,2006,22(1):1-2.
[4]刘庆凤,潘虹,赵洪利.π-正则半群上的最小π-群同余及最小群同余[J].五邑大学学报:自然科学版,2009,23(2):75-78.
[5]Howie J M.Fundamentals of semigroup theory[M].Ox⁃ford University Press,New York,1995.
[6]田振际,李生有.π-逆半群的若干等价条件[J].兰州铁道学院学报:自然科学版,2000,19(4):42-44.
[7]Hanumantha Rao S,Lakshmi P.Group congruences on eventually regular semigroups[J].J Austral Math Soc(Se⁃ries A),1998,45:320-325.
[8]田振际,魏和中.π-逆半群上的几个有限性条件[J].兰州铁道学院学报:自然科学版,1998,17(4):117-120.
The Group Congruence and Minimum Group Congruence on Quasi-inverse Semigroups
JIAO Hongying,LIU Weijiang
(
School of Sciences,Air Force Engineering University,Xi’an710051,China)
A full and self-conjugate subsemigroup of a quasi-inverse semigroup S are used in this paper.Then,the group congruence and minimum group congruence on the semigroup S is obtained.
quasi-inverse semigroup;group congruences;the minimum group congruence;self-conjugate
O 152.7
A
1674-4942(2011)03-0250-03
2011-05-02
毕和平

