纵向数据中伪似然方程的根的相合性

闫 莉，陈淑兰

（广西大学 数学与信息科学学院，广西 南宁 530004）

纵向数据中伪似然方程的根的相合性

闫 莉，陈淑兰

（广西大学 数学与信息科学学院，广西 南宁 530004）

研究了伪似然方程的根的渐近存在性和相合性大样本性质.伪似然方程是研究纵向数据的一种方法，它是广义估计方程（GEE）的一种推广，用适当的矩阵去估计相关阵，这也是研究意义所在.自从Shao（1999）定义伪似然方程以来，其大样本性质也不断完善.本文证明了在一定条件下伪似然方程的根的渐近存在性及相合性.

纵向数据；伪似然方程；渐近存在性；相合性

1 引言

自从Liang和zerge用广义线性模型去分析纵向数据和分类相关数据，由此发展为广义估计方程（GEE），GEE的渐进结果在文[1]和[2]中逐渐完善.1999年，Shao引入了伪似然方程，文[3]具体研究了其渐进结果.

在纵向数据中，观测向量（yij，Xi）j表示第i个个体的第j次观测值，每个个体i重复测量m次，Xij是p维协变量，β为p维未知参数，μ是连续可微的联系函数且μ＞0，本文假设不同个体的观测值是独立的，同一个体内部观测值是相关的，并且考虑的是自然联系函数，m有界n趋向于∞的情况下，伪似然方程的根的渐近存在性和相合性.

为了后文的方便，引入下列记号：

2 主要结果及证明

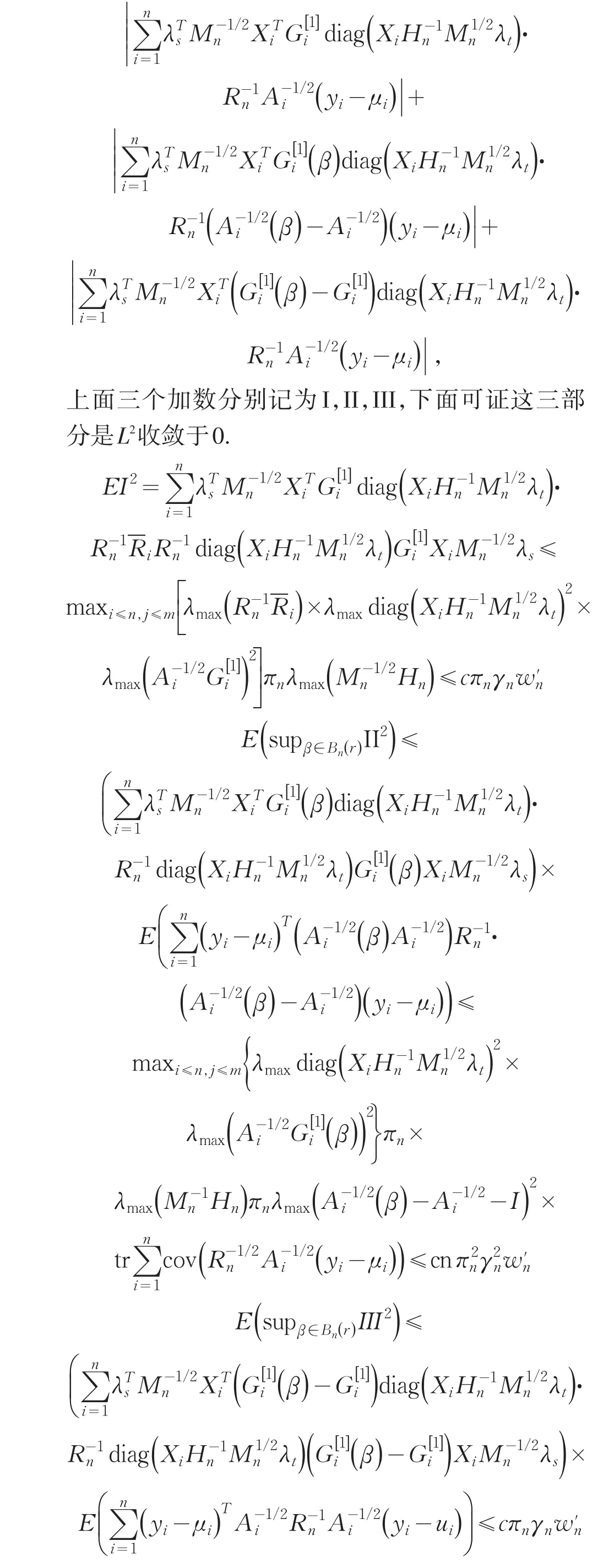
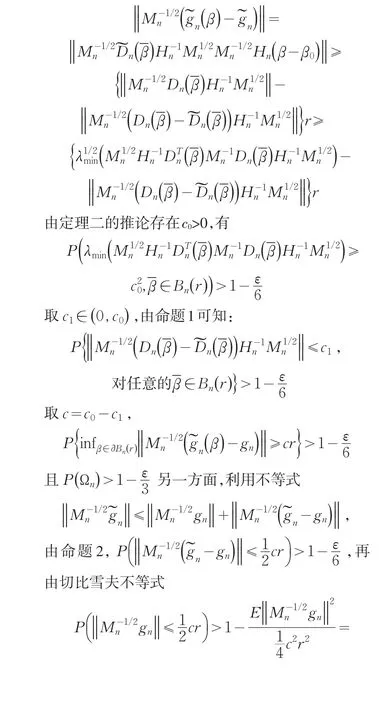
[1]Xie M,Yang Y.Asymptotics for generalized estimating equations with large cluster sizes[J].Ann Statist,2003,31(1):310-347.

[2]Chen K,Hu I,Ying Z.Strong consistency of maximum quasi-likelihood estimation in generalized linear models with fixed and adaptive designs[J].Ann Statist,1999,27:1155-1163.

[3]Balan R M,Schiopu-Kratina I.Asymptotic Results With Generalized Estimating Equations for Longitudinal Date[J].Ann Statist,2005,33(2):522-541.

[4]Liang K Y,Zerge S L.Longitudinal data analysis using gen⁃

eralized linear models[J].Biometrics,1986,73:13-22.

Consistency of Pseudo-likelihood Equation of Longitudinal Data

YAN Li，CHEN Shulan
（College of Mathematics and Information Sciences，Guangxi University，Nanning530004，China）

The asymptotic existence and consistency of the solutions of pseudo-likelihood equation are studied in this paper.Pseudo-likelihood equation is the extension of the generalized estimating equation,which is an approach used to study longitudinal data.The use of appropriate matrix to estimate the correlation matrix that is the researching signifi⁃cance we need.Large sample properties of pseudo-likelihood equation have been enriched since the definition of proper⁃ties of pseudo-likelihood equation is proposed by shao.The proof of asymptotic existence and consistency of the solu⁃tions of pseudo-likelihood equation is given in some condition in this article.

Longitudinal date；Pseudo-likelihood equation；Asymptotic existence；Consistency

O 212.1

A

1674-4942（2011）03-0237-05

2011-05-01

国家自然科学基金资助项目（11061002）

毕和平