实物复合期权模型在采矿权定价中的应用

王华强，刘黎明

（首都经济贸易大学，北京100070）

在评估实务中，采矿权的估价方法主要是采用贴现现金流法。该方法的评估原理，是选取某一适当的折现率对未来预期现金流进行折现。Fisher提出的这种贴现现金流方法，由于简单实用而在实务中被广泛使用，但是它的缺点很明显，尤其是面对不确定性高的采矿权。矿产品的价格具有随机波动特点，所以无法准确预测未来的现金流。另一方面，在长达几年甚至十几年的开采期内，选择一个准确的贴现率是很困难的。这种静态的评估方法，没有考虑在矿产开采过程中的不确定性。

随着期权定价理论在实物资产领域的应用，实物期权理论逐渐形成。在国外，学者已经将实物期权应用到矿山整体价值评估［1］、近海石油租赁合约定价［2］、森林资源投资［3］等领域，但是这些研究中，没有采矿权的估价。国内学者自20世纪90年代开始，逐渐将实物期权用于定价方面的应用研究［4－8］，其领域涉及：自然资源评估、环境项目投资、矿业权评估、矿产资源投资策略等。虽然国内学者将期权定价理论应用在矿产权方面，但应用中存在一些不足，主要表现在：仅仅将实物资产中的各项参数直接或稍加修正应用到B－S模型；将矿产权价值与矿产资源收益的概念等同；不考虑矿产生产的时滞性；不加条件的直接使用期权的可加性等。

邹绍辉等［8］提出，矿产企业最终获得的收益应当补偿其矿产投资资本的机会成本。虽然采矿权持有者具有开采矿产资源并出售矿产品的权利，但是并不能获得全部收益，而是应付出一部分以采矿权为名义的收益。因此，在采矿权的期权模型中，标的资产是矿产品的净收益，敲定价格是投资的机会成本。尽管邹绍辉等指出矿产资源采矿权是一个多期多阶段的复合看涨期权，但是在文献中的期权模型并非严格的复合期权模型。另外，机会成本反应了投资的最大收益。在理性市场条件下，敲定价格不应是机会成本而应是预期收益。本文旨在分析采矿权的复合期权属性，建立采矿权定价的复合期权模型，并实证分析，为采矿权投资决策提供依据。

1 采矿权建模

复合期权的研究起源于Black和Scholes在期权定价方面的开创性工作。他们将股票视为写在公司价值上的期权，若公司价值可视为写在公司债券上的期权，则股票便是写在公司债券上的复合期权［9］。Geske把公司股票看作写在公司资产价值上的欧式看涨期权，再在欧式看涨期权上建模为复合期权，并导出了简单复合欧式期权模型封闭形式的解［10］。Geske给出的简单复合期权定价的一般公式，成为复合期权发展的基础。复合期权本质上是一系列权利的嵌套，适合描述涉及序列决策问题。在实践中，矿产企业按年度决定是否执行采矿权，如果选择执行采矿权，将主要进行两步投资：第一，开采阶段，在这一阶段需要投入资金，完成人力资源筹备、矿石开采等工作，此时投入资金称之为开采成本；第二，选矿阶段，在这一阶段需要投入资金，对第一阶段的矿石进行冶炼，最终获得矿产品并出售，此阶段投入资金称之为选矿成本，两次投资总和为总投资。

采矿权持有者在采矿权起始日拥有一种期权，能够在某开采日投资开采，称为开采期权。如果持有者决定投资开采，便又购买到一种看涨期权，该期权使得采矿权持有者拥有在选矿阶段结束后，出售矿产品并获利的权利，称为选矿期权。对于选矿的期权，矿产企业在开采时刻拥有一种是否进行矿石冶炼的权利，而非义务。因此，选矿期权就是一份以矿产资源价值，即矿产品销售的净收益为标的资产，以选矿资金的预期收益为敲定价格的看涨期权。对于开采期权，矿产企业在采矿权起始时刻，拥有一种在某时刻是否进行矿石开采的权利，而非义务。因此，开采期权是一份以选矿期权为标的资产，以采矿资金的预期收益为敲定价格的看涨期权。这样，采矿权是一份在看涨期权的基础上，又拥有一份看涨期权的期权。因此，采矿权持有者拥有的不是简单的欧式看涨期权，而是一份两期复合期权。

首先对模型的符号进行设定：

P为年度矿产品的价值；C和I为对应开采成本和选矿成本；S为矿产品收益，S＝P－I；采矿权期限为n年，年度时刻为Ti，Ti＝0，1，2，3，…，n；Vi、为Ti时刻的采矿权价值；Ti时刻的开采成本的预期收益为K1，开采的产品总成本的预期收益为K2，K1＝C×α，K2＝I×α，其中α为预期收益比例。

为了建立采矿权的定价模型，本文需要对矿产企业的经营状况进行假设，具体内容如下：

假设1：年初支付开采成本，年末支付选矿成本，且其预期收益比例为常数；由此假设可知，企业一旦执行开采期权，进入采矿阶段，获得的选矿期权的期限为一年。

假设2：最终行权日不超过采矿权期满日。

假设3：开采和选矿成本以现有技术水平为基准，即投资成本不变。

假设4：矿产品净收益S的分布服从几何布朗运动。

假设5：无风险利率r为常数。

据前文分析，每年的采矿权可以看作是复合期权，所以采矿权的价格是按年度系列计算的复合期权价格的总和。下文首先以开开采时刻为Ti为例，计算该时刻复合期权的价格，然后求总和得到采矿权的价值。

又，在t＝Ti时刻相应的终止条件为：

因此，在区域Ω1上的期权定价公式：

由此，可得到开采时刻为Ti的复合期权价格：

其中

参数a1i中S＊是满足方程：

其中

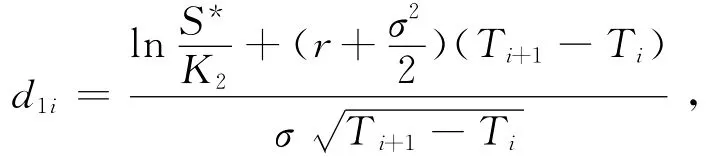
M（a，b；ρ）表示二维累计正态分布函数：M（a，b；ρ）＝p｛X≤a，Y ≤b｝

这里X ～N（0，1）、Y ～N（0，1）都是标准正态分布，Cov（X，Y）＝ρ，（0＜ρ＜1）。

由上述分析可知，某一年的采矿权价格，可以由简单复合期权模型得到，那么整个期限采矿权价格，即为逐年的复合期权价格之和：

相关参数同上。

2 实证研究

2.1 参数计算

实例：广实会计师事务所有限公司为云南达亚有色金属有限公司狮子山铜矿采矿权进行评估。其主要参数总结如表1所示。

因为评估计算期铜精矿产量共30351．23t，且矿产的服务年限为9．52年，所以可以得到铜精矿的生产规模为3188．15t／a。又有铜精矿的不含税价格，可得年度矿产品的价值为124018345．82元；因为评估计算期铜矿石产量共491万t，且矿产的服务年限为9．52年，所以可以得到铜矿石的生产规模为515756．30t／a。又有单位总成本费用，可得狮子山铜矿年生产总成本为98277363．45元。所以，矿产资源年收益为25740982．37元。按照矿产生产的实际情况，铜精矿的生产过程包括采矿过程和选矿过程。根据矿产生产的经验数据，一般可以认为，地下开采成本与选矿成本比例为2∶1。因此，狮子山铜矿的年开采成本为65518242．30元，相应选矿成本为32759121．15元。

本文选取了证监会行业分类中有色金属矿采选业的历年销售毛利率，以行业的平均毛利率来表示投资预期收益比率，将其平均值23．61%作为投资预期收益比率。无风险收益可由十年期2009国债27（019927）的年利率3．68%来代替。根据铜价历史数据，本文计算得到年波动率为0．29714。期权定价参数总结如表2所示。

表1 评估参数表

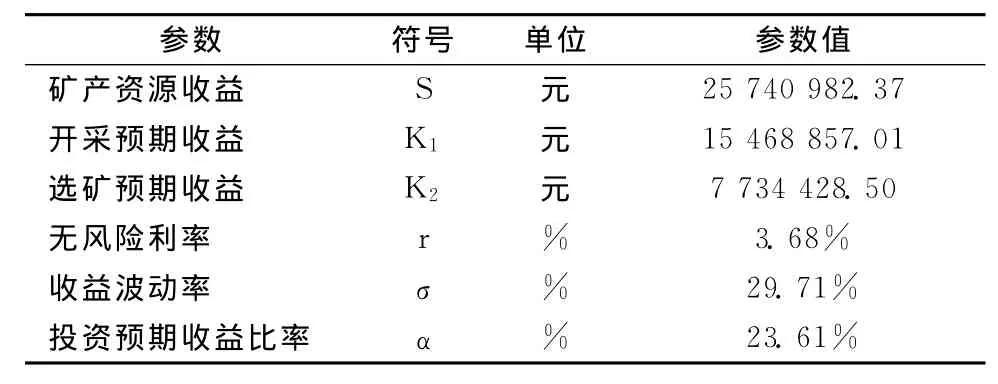
表2 期权定价参数表

2.2 定价实证结果

在采矿权期期初，采矿权持有者具有一年的基建时间。因此，第一个复合期权是2010年9月30日的，此刻距离评估基准日是1年，距离采矿权到期日有9．5年。依此类推，将在此后每年9月30日遇到一个复合期权，直到2019年9月30日。2019年9月30日为采矿权期限内最后一个复合期权，其成熟期为2020年3月31日。由上述推导的采矿权定价公式，首先应该确定协方差、临界矿产资源收益值，以及其他累计分布函数的参数值，然后代入公式中计算结果。在计算中，由于本文选例的特殊性，矿山服务年限是9．52年，所以在计算最后半年的复合期权时，标的资产和敲定价格都相应减半。二维标准正态累计分布函数M（a1i，b1i；ρi）和 M（a2i，b2i；ρi），表3中分别以 M1和M2代替。本文通过数学软件Matlab计算复合期权的各参数值，所得结果如表3所示。

表3 常数波动率复合期权评估表

由表3得到采矿权的价值约为4216．61万元，相对于贴现现金流评估值为2228．81万元，复合期权模型得到的采矿权的价值高于贴现现金流法得到的采矿权价格。如前所述，实物期权思想认为，不确定性增加了矿产资源投资的价值。复合期权模型考虑了未来信息的价值、矿产企业经营活动的灵活性，并且认为这些因素是有价值的。而贴现现金流评估认为，未来信息价值固定，假定了企业的经营活动一成不变，并否定了不确定性的价值。所以，在复合期权模型中采矿权的价值，高于在贴现现金流贴现模型中。

贴现现金流法认为，企业有着固定的利润和成本，不考虑时间的价值，这种不科学的方法不能作为投资决策依据。复合期权定价方法，综合考虑到这些不确定性，得到的采矿权的价值高于市场上的评估价格，即市场存在负溢价。这说明市场的采矿权价格存在着价值低估。那么，对于一家预期收益率为行业平均毛利率23．61%的企业，该采矿权存在价值投资的空间。

3 总结

在采矿权评估实务中，贴现现金流方法对采矿权的估计，往往需要对未来有一定的预期和严格的假设，不能考虑和处理矿产开采面临的不确定性和管理柔性。由于这种方法缺少不确定的价值，造成估价不够准确。近期文献利用期权对采矿权的定价研究，集中在简单期权上，不能充分考虑到矿产企业开采的实际情况，对采矿权的评估不够准确。本文基于复合期权理论，将采矿权看作是一系列年度的复合看涨期权的总和。在一定的假设下，推导出基于复合期权的采矿权定价公式，并实证分析，发现复合期权模型估值更加符合实际。复合期权定价方法得到的采矿权的价值，高于市场的评估价格，即负溢价，这说明市场的采矿权价格存在价值低估，采矿权具有投资价值。

［1］ Brennan，Schwarts．Evaluating Natural Resource Investments［J］．The Journal of Business，1985，58 （2）：135－157．

［2］ Paddock，Siegel．Option Valuation of Claims on Real Assets：The Case of Offshore Petroleum Leases ［J］．The Quarterly Journal of Economics，1988，103 （3）：479－508．

［3］ Margaret Insley．A Real Options Approach to the Valuation of a Forestry Investment［J］．Journal of Environmental E－conomics and Management．2002，44：471－492．

［4］ 柯昌文，王宗军．实物期权在自然资源投资中的应用 ［J］．华东经济管理，2007，21 （9）：95－98．

［5］ 张华伦，曾韦韦，李秉祥．环境项目投资的实物期权方法［J］．统计与决策，2006，（9）：31－32．

［6］ 刘朝马，廖作鸿．矿业权评估的实物期权方法研究初探［J］．中国矿业，2003，12 （1）：16－18．

［7］ 朱磊，范英，魏一鸣．基于实物期权理论的矿产资源最优投资策略模型 ［J］．中国管理科学，2009，17 （2）：36－41．

［8］ 邹绍辉．基于期权的矿产资源采矿权价值形成机理研究［J］．金属矿山，2009，（10）：35－38．

［9］ Black，F，Scholes，M．The Pricing of Options and Corporate Liabilities ［J］．The Journal of Political Economy，1973，81 （3）：637－654．

［10］ Robert Geske．The valuation of compound options ［J］．The Journal of Financial and Quantitative Analysis，1977，12 （4）：541－552．