分路段交通状态模式元胞传递模型

弓晋丽，杨东援，彭贤武

（1.同济大学 交通运输工程学院，上海201804；2.长沙理工大学 交通运输工程学院，湖南 长沙410114；3.三一重工股份有限公司，湖南 长沙410100）

由城市快速路上布置的大量固定检测线圈检测到的数据可为交通流分析提供大量可靠的信息，但由于固定检测线圈只能获得断面交通参数数据，无法得到路段交通参数数据，因此无法直接将其应用于路段交通流运行状况分析中.为此，近年来国内外许多研究者提出了多种交通流模型，旨在模拟交通状态演变过程，用于路段交通流参数估计.其中，由Daganzo于1993 年 提 出［1］的 元 胞 传 递 模 型（cell transmission model，CTM）能够再现许多重要的交通现象（如“冲击波”行为和拥挤波的向后传播等），具有易于理解的优点，因此得到了广泛的应用.但Daganzo最初提出的CTM 模型存在一定的缺陷：它将道路等分为等长的路段，限制了CTM 模型在实际交通中的应用.Muñoz［2］提出了改进的CTM 模型（modified cell transmission model，MCTM），实现了道路非等长划分，增加了CTM 模型的适用性.随后，Sun［3］根据元胞拓扑衔接方式的不同，提出了城市快速路上下匝道流量传输模型.接着，Gomes等［4］提出非对 称 的CTM 模 型（asymmetric cell transmission model，ACTM），用于进行匝道控制策略的优化比选.

本文在对交通流动态特性的“可观测性”在不同路段交通状态下差异性分析的基础上，提出了城市快速路分模式CTM 模型.该模型以固定检测线圈为信息来源，更新了流量传输模型，将其表示为不同路段交通状态模式下的分段函数形式，并针对城市快速路新构建了下匝道流量传输模型.

1 分模式CTM 模型构建

1.1 路段交通状态模式的划分

本文采用模糊C－均值聚类算法［5－7］，将检测线圈断面交通状态根据流量—占有率关系分为畅通状态和拥挤状态（图1）.其中，畅通状态是指速度较大而占有率较低所对应的状态（图1中圆圈所标注的部分）；拥挤状态指速度较小而占有率较高所对应的状态（图1中十字符号所标注的部分）.

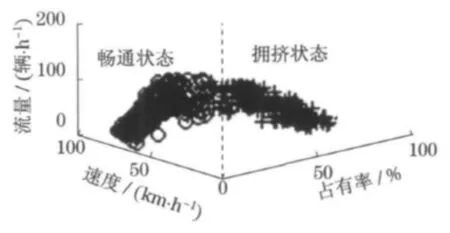
图1 交通定性状态模糊C－均值聚类Fig.1 Fuzzy C－means for traffic qualified state

在得到检测线圈断面的交通定性状态后，为判别路段交通状态模式，特提出以下假设：①如果路段上下游检测线圈断面交通状态一致，则认为路段交通状态单一且与检测线圈断面状态保持一致；②如果路段上下游检测线圈断面交通状态不一致，则假设路段内最多存在一处状态转换区域（由于城市快速路检测线圈布置比较密集，因此忽略上下游检测线圈无法检测到的路段内小范围的拥挤）.据此，将路段交通状态模式划分为4种模式：上游畅通－下游畅通（G1）；上游拥挤－下游拥挤（G2）；上游拥挤－下游畅通（G3）；上游畅通－下游拥挤（G4）.2004 年，文献［2］指出不同模式下交通流动态特性的差异表现为“可观测性（Observability）”的不同（详见表1）.

表1 分模式路段“可观测性”Tab.1 The road‘obersevability’under different patterns

1.2 模型的构建

分模式CTM 模型主体包括4部分：车流量守恒方程，主线流量传输模型，上匝道流量传输模型，下匝道流量传输模型.为实现元胞划分长度各不相同，模型采用密度作为路段交通状态指标，代替元胞内车辆数变量.元胞划分如图2所示.图中，q表示交通流量，r表示上匝道流量，f表示下匝道流量，ρ表示交通密度，d表示上匝道交通需求量，a表示下匝道交通需求量.

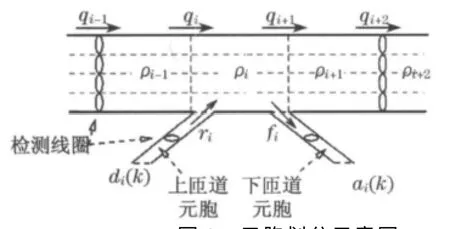
图2 元胞划分示意图Fig.2 Scheme for cell partitioning

1.2.1 车流量守恒方程

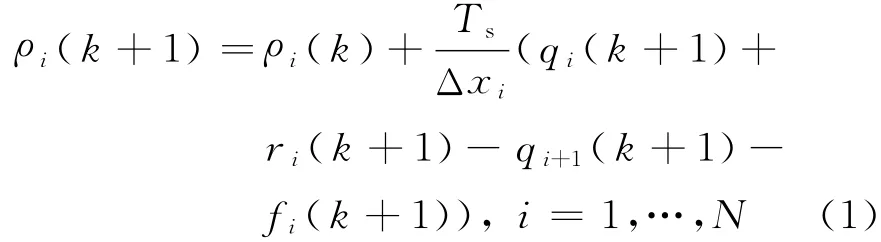
式中：Ts表示采样周期（时间间隔）；ρi（k＋1）表示第k＋1个采样间隔Ts［k，k＋1）内元胞i的密度；qi（k＋1）表示k＋1时间间隔内从元胞i－1流入元胞i的流量；ri（k＋1）表示k＋1时间间隔内由元胞i所含上匝道进入主线元胞i流量；fi（k＋1）表示k＋1时间间隔内由元胞i所含下匝道离开主线元胞i流量；Δxi表示元胞长度.

1.2.2 主线流量传输模型

考虑上下匝道与主线间相互影响，引入上匝道流量融合因子γ和下匝道流量分离因子λ修复主线密度

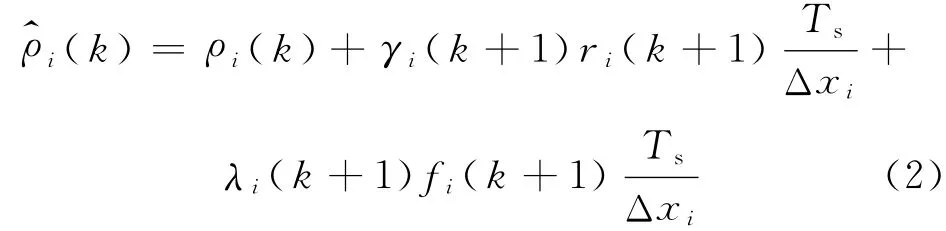
式中：γi∈［0，1］表示元胞i中上匝道流量融合因子，意指车辆从上匝道元胞被容许进入主线元胞i的最大比例；λi∈［0，1］表示元胞i中下匝道流量分离因子，取0值时表明元胞i中不存在下匝道.

流量传输模型为

式中：Sdi－1（k＋1）表示k＋1 时间间隔内由元胞i－1所在路段下游检测线圈信息标定得到的元胞i－1产生流量；Rui（k＋1）表示k＋1时间间隔内由元胞i所在路段上游检测线圈信息标定得到的元胞i吸引流量.

式（3）中Sdi－1（k＋1）和Rui（k＋1）分别由下式计算：

式中：QM，di－1表示由元胞i－1所在路段下游线圈检测信息标定得到的元胞i－1最大通行能力；vdi－1表示与QM，di－1标定方式一致时元胞i－1自由流速度；QM，ui表示由元胞i所在路段上游线圈检测信息标定得到的元胞i最大通行能力；ωui和ρJ，ui分别表示由元胞i所在路段上游线圈检测信息标定得到的元胞i拥挤波动传播速度和阻塞密度.

主线流量传输模型反映了不同路段交通状态模式下，交通信息“可观测性”的不同：G1模式下元胞i所在路段处于畅通状态，元胞流量qi由下游检测线圈信息标定，等于元胞i－1产生流量；G2和G3模式下元胞i所在路段存在拥挤，元胞流量qi由上游检测线圈信息标定，等于元胞i吸引流量；G4模式时与以往CTM 模型保持一致，为元胞i－1所提供流量和元胞i可接受流量的最小值.

1.2.3 上匝道流量传输模型

式中：RM，i为上匝道通行能力；lri（k）为上匝道排队车辆数；di（k）为上匝道交通需求量；ξi为元胞i所含上匝道流量分配因子，反映主线元胞i容量对所含上匝道车流量的制约作用.上匝道排队车辆数传输模型为

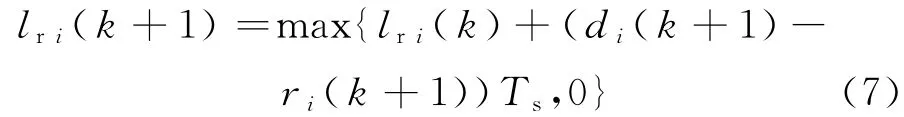
1.2.4 下匝道流量传输模型

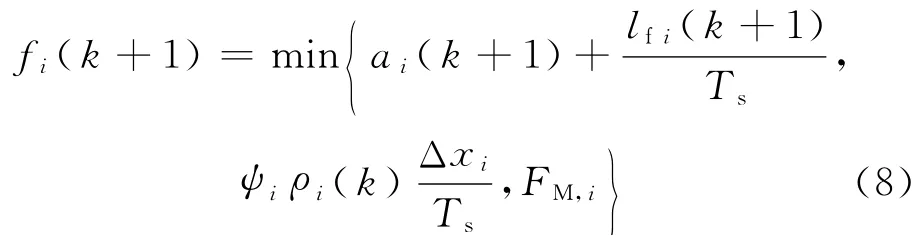
式中：FM，i为下匝道通行能力；lfi（k）为下匝道排队车辆数；ai（k）为下匝道交通需求量；ψi为元胞i所含下匝道流量分配因子，反映主线元胞i最多能够为下匝道提供的流量比例.下匝道滞留车辆数传输模型为

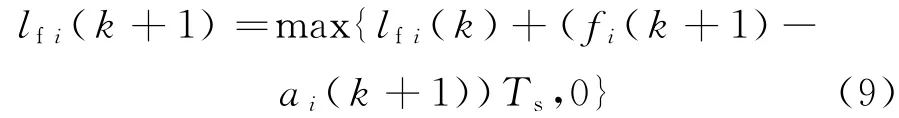
2 模型参数标定

模型在运算前，应先基于修复后的检测线圈数据［8］对模型参数进行标定，其所需标定参数包括基本图参数、匝道参数及模型控制变量等.

2.1 基本图参数

为实现基本图标定，需先将检测得到的交通量、时间平均速度和占有率转换为空间平均速度和密度［9－10］.根据流密速关系，得到密度的估算式为

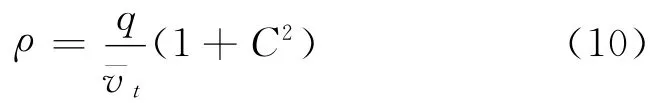
式中：q为车流量；v—t为平均速度；C为速度变异系数.

假设模型中基本图形满足三角形形状，则基本图参数自由流速度vf、拥挤波速ω、通行能力QM和阻塞密度ρJ 的标定方法为：①采用交通状态分类器对线圈数据样本进行交通状态判别；②通行能力QM的标定，取样本数据中流量最大值为通行能力QM的标定值；③自由流速度vf的标定，使用最小二乘法拟合自由流样本集内密度—流量函数关系，用函数斜率值估计自由流速度；④拥挤波速ω的标定，以vf除以某固定比值得到拥挤波速（Wei－Hua Lin 使用1993 年美国加州I－880公路数据对CTM 中vf／ω进行了比选测试，结论认为当两者之比位于［2，6］之间时模型仿真结果较理想［11］）；⑤计算分界密度ρm 与阻塞密 度ρJ，ρm ＝QM／vf，ρJ ＝ρm＋QM／ω.分 模 式CTM 模型三角形基本图见图3.

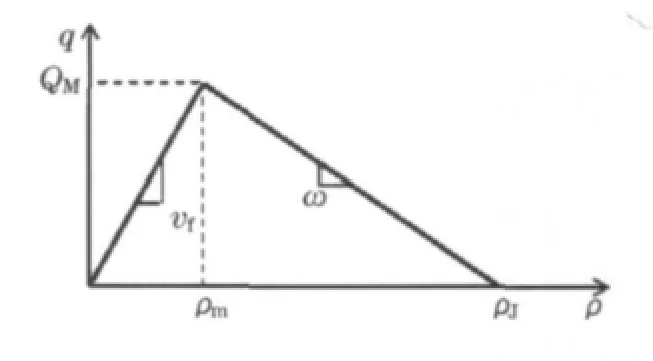
图3 分模式CTM 模型三角形基本图Fig.3 The triangle fundamental graph for pattern CTM

2.2 上下匝道参数

上匝道流量分配因子ξi（k）由k时间间隔内元胞i所在路段上游检测线圈流量qui（k）、下游检测线圈流量qdi（k）和上匝道检测线圈流量标定，其计算式为

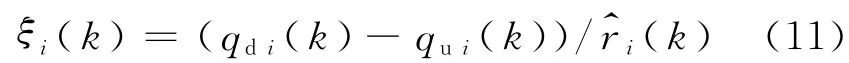
上匝道流量融合因子γi（k）使用k时间间隔内元胞i所在路段上游线圈检测流量qui（k）和匝道检测数据标定，其计算式为

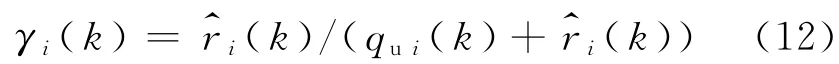
下匝道流量分配因子ψi（k）使用k时间间隔内元胞i所在路段上游线圈检测流量qui（k）、下游线圈检测流量qdi（k）和下匝道检测流量标定，其计算式为

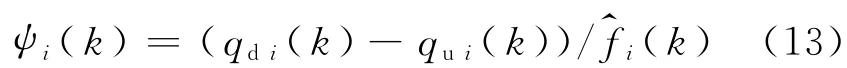
下匝道流量分离因子λi（k）使用k时间间隔内元胞i下游线圈检测流量qdi（k）和下匝道检测流量标定，其计算式为

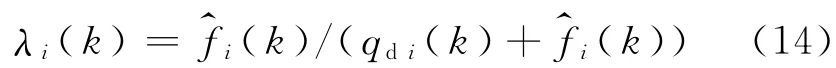
元胞i所含上匝道交通产生需求量di和下匝道交通吸引需求量ai可分别由相应上下匝道检测线圈流量标定.上匝道通行能力RM，i取相应上匝道流量检测数据的最大值，下匝道通行能力FM，i取相应下匝道流量检测数据的最大值.

2.3 其他模型参数

初始密度是指模型开始运算前各个元胞的密度ρi（0）.模型运算中以初始时间段内密度估算值作为初始密度的近似值.路段输入流量使用路段最上游线圈检测流量标定；设路段共划分为N个元胞，则输出流量使用第N个元胞所在路段的下游线圈检测流量标定.上述方法为一般性建议，实际使用中需根据具体数据进一步调整分析.

3 实证分析

城市快速路元胞划分需遵循以下原则［12－14］：①单个元胞所含上匝道数量不超过1个，且如果元胞内包含上匝道，则上匝道一定位于元胞的开始位置；②单个元胞包含的下匝道数量不超过1 个，且如果元胞内包含下匝道，则下匝道一定位于元胞的结束位置；③单个元胞包含的检测线圈数量不超过1个；④单个元胞车道数一致.意即道路车道数增加或减少位置需断开，划分为不同元胞；⑤为加快模型运算速度，同时保证采样时间间隔Ts满足条件，元 胞长度Δxi尽量取较大值.

3.1 模型性能比较

为对MCTM 模型、ACTM 模型和分模式CTM模型性能进行比较，本文选取上海南北高架东侧DX02—DX05间共1 302m 长的路段作为测试路段（图4）.根据以上原则将其划分为5个元胞，c1—c5元胞长度分别为249，173，466，158和276m.

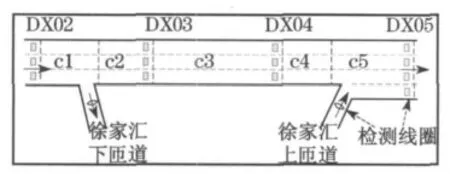
图4 上海南北高架部分路段元胞划分示意图Fig.4 Scheme for parts of Shanghai North－South Expressway

仿真步长的设定将影响运算的次数和运算的时间.如文献［1］中所描述，CTM 模型假定仿真步长Tm满足条 件，因 此 本 文 以做为仿真步长.使用Matlab编程分别对MCTM，ACTM 和分模式CTM 模型进行仿真运算，仿真时段选取2009年3月20日上午6：00～12：00（观察表明该时间段内无交通事故发生，但有多次拥挤发生）.将该时间段内DX02和DX05检测线圈数据以及徐家汇下匝道和徐家汇上匝道处的检测线圈数据作为输入，使用各个模型对路段交通参数进行估算.定义序列｛yi｝的平均百分比误差Empe描述仿真结果与真实值｛yi｝的偏差，其计算公式为

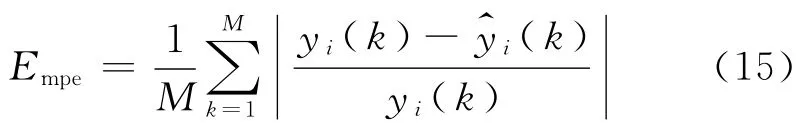
运算结果显示：c1仿真结果与DX02测定值比较，密度平均百分比误差为15.81%，流量平均百分比误差为7.36%，速度平均百分比误差为15.47%.如表2所示，模型对比显示表明，分模式CTM 模型密度和速度的Empe均小于平均值，分模式CTM 模型结果较优.根据分模式CTM 模型的仿真结果得到的交通状态和测量数据得到的交通定性状态对比如图5所示.图中，浅色部分表示畅通状态，深色部分表示拥挤状态.可以看到，仿真结果与实际道路状态基本保持一致，表明分模式CTM 模型能很好地模拟现实情况.

图5 交通状态分模式CTM 模型仿真结果与测量结果对比Fig.5 Comparison between actual detected traffic state against simulation result

3.2 大规模路段检测数据验证分析

选取上海南北高架东侧DX01—DX19间路段为大规模验算实例，将其划分成30个元胞，元胞平均长度为0.261km（图6）.图中刻度上数字表示各个元胞长度；灰色位置用于标示检测线圈所在位置；各元胞上所标白色数字表示元胞编号.以2009年3月20日至29日连续10d的线圈数据为例，10d中包括6个工作日和4个周末.

为进行分模式CTM 模型的仿真运算，首先用上文中模型参数标定方法，基于10d内检测线圈数据对各路段上下游基本图参数进行标定，使用同样的数据建立分模式CTM 模型进行仿真，可获得30个元胞的密度、空间平均速度及流量.如表3所示，10d模型运算结果与检测线圈测量值的平均百分比误差计算结果表明，密度估算结果误差为20%左右，流量估计结果误差为10%左右，表明仿真效果较理想.速度误差偏大主要原因在于CTM 模型基本假设认为自由流阶段速度等于定值，与实际测量结果表明自由流阶段速度具有随机性存在差异［15］.

表2 交通参数仿真结果与测量值的平均百分比误差比较Tab.2 MPE of actual detected traffic parameters against simulation result %

图6 上海南北高架东侧元胞划分示意图（单位：m）Fig.6 Scheme for cell partition on eastern side of Shanghai North－South Expressway

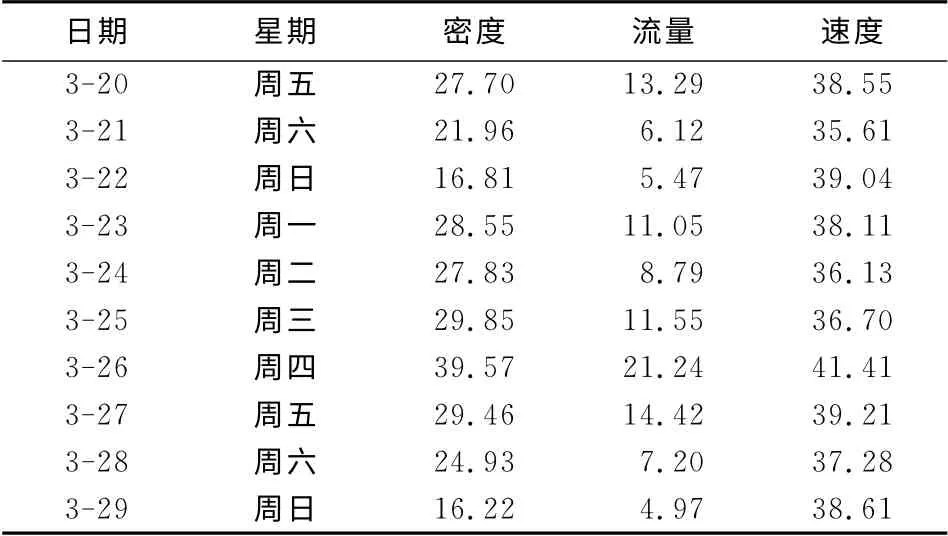
表3 模型仿真结果与线圈测量值平均百分比误差Tab.3 MPE of simulation result against actual detected data %

4 结论

本文对城市快速路宏观CTM 模型进行了研究.该模型基于定点检测线圈数据，实现了城市快速路交通状态演变过程的模拟和路段交通参数的估计.

在采用模糊C－均值聚类算法，将路段上下游检测线圈断面交通状态根据流量—占有率关系分为畅通状态和拥挤状态后，将路段交通状态模式划分为4种模式.根据不同路段交通状态模式下交通流信息“可观测性”不同提出了分模式CTM 模型，该模型将流量传输模型表示为不同路段交通状态模式下的分段函数形式；并新构建了城市快速路下匝道流量传输模型.最后，使用MATLAB 编程对南北高架东侧DX02—DX05间共1 302m 长的路段进行了实例测试.结果表明，与MCTM 和ACTM 比较，由分模式CTM 模型计算获得的密度和速度的平均百分比误差均小于平均值，能较好地模拟现实情况.为实现分模式CTM 模型在大规模数据集上的应用，本文以上海南北高架东侧DX01—DX19路段为例，使用10检测数据进行了仿真运算.结果表明，密度估算结果平均百分比误差为20%左右，流量估算结果平均百分比误差为10%左右，仿真效果较理想.

［1］ Daganzo C F.The cell transmission model：a dynamic representation of highway traffic consistent with the hydrodynamic theory［J］.Transportation Research Part B：Methodological，1994，28（4）：269.

［2］ LAURA Matiana Muñoz.Macroscopic modeling and identification of freeway traffic flow［D］.Berkeley：University of California，2004.

［3］ SUN Xiaotian.Modeling，estimation，and control of freeway traffic flow［D］.Berkeley：University of California，2005.

［4］ Gomes G，Hhrowitz R.Optimal freeway ramp metering using the asymmetric cell transmission model［J］.Transportation Research：Part C，2006，14（4）：244.

［5］ 孙亚，钱洪波，叶亮.数据挖掘算法在交通状态量化及识别的应用［J］.计算机应用，2008，28（3）：738.SUN Ya，QIAN Hongbo，YE Liang.Application of data mining in traffic state quantification and recognition［J］.Computer Application，2008，28（3）：738.

［6］ 王辉，王孝坤，王权.一种交通流状态智能推理系统［J］.系统工程，2007，25（12）：7.WANG Hui，WANG Xiaokun，WANG Quan.An intelligent inference system of the traffic flow status［J］.Systems Engineering，2007，25（12）：7.

［7］ 王辉.基于模糊行程时间的车辆配送问题研究［D］.上海：同济大学交通运输工程学院，2008.WANG Hui.Study on vehicle routing problems with fuzzy travel time ［D ］.Shanghai： Tongji University. College of Transportation Engineering，2008.

［8］ 孙亚.基于数据质量的定点交通信息采集系统研究［D］.上海：同济大学交通运输工程学院，2008.SUN Ya.Study on fixed traffic information collection system based on data quality［D］.Shanghai：Tongji University.College of Transportation Engineering，2008.

［9］ 胡小文，杨东援.城市快速道路交通流密度的估计［J］.交通运输系统工程与信息，2008，8（3）：79.HU Xiaowen，YANG Dongyuan.Estimation of traffic density on urban freeways［J］.Journal of Transportation Systems Engineering and Information Technology，2008，8（3）：79.

［10］ May A D.Traffic flow fundamentals［M］.［S.l.］：Prentice Hall，1990.

［11］ LIN Weihua，Dike Ahanotu. Validating the basic cell transmission model on a single freeway link［M］.Berkeley：University of California，1994.

［12］ Cayford R，Lin W H，Daganzo C F.The netcell simulation package technical description，technical report［R］.Berkeley：University of California，1997.

［13］ TOPL Group.Cimsim traffic Macro－simulator for MATLAB［EB／OL］.［2010－04－25］.http：∥Path.Berkeley.Edu／Topl／Software.Html.

［14］ Alex A Kurzhanskiy，Pravin Varaiya.Ctmsim —an interactive macroscopic freeway traffic simulator ［R］.Berkeley：Department of Electrical Engineering and Computer Sciences，2008.

［15］ Gomes G，Horovitz R，Kurzhanskiy A，et al.Behavior of the cell transmission model and effectiveness of ramp metering［J］.Transportation Research，2008，16（4）：485.