两并列方形高层建筑局部风压干扰特性
韩 宁,顾 明
(同济大学 土木工程防灾国家重点实验室,上海200092)
由于建筑物之间的流场干扰,作用于建筑物上的风压与孤立状态时相比会有显著变化,建筑物各个面的风压将会变得更加复杂.过去几十年中,国内外对高层建筑干扰效应进行了大量的研究.文献[1]对影响干扰效应的参数进行了系统的总结,此后,文献[2-5]针对3个干扰建筑做了详细的研究,主要分析了动力干扰效应和干扰相关性.对于2个建筑物处于并列位置的干扰效应研究,文献[6]分析了施扰方柱为4种不同尺寸比(即0.5,1.0,1.5和2.0)且位于不同特定位置处时对于测试方柱振动反应的影响,指出尺寸比等于1.0是临界值,当尺寸比小于等于1.0时,其改变对于测试方柱振动幅值的影响并不显著,但是当尺寸比大于1.0且有较高的折减速度(大于12)时,施扰方柱尺寸比改变将会使受扰方柱产生较大幅值的振动.文献[7]通过风洞试验和数值模拟对比分析了错列布置时2个临近建筑的风压干扰效应,但其仅研究了特定高度处若干测点的变化.文献[8]分析了2个不同截面尺寸方柱并列布置时其周围流场变化和气动力分布,研究的横向间距介于1.12~2.50之间.文献[9]通过数值模拟方法分析了2个并列方柱不同间距比时的流场特征,发现间距比存在一个阈值,小于该值时会出现双稳态偏流现象,但其没有考虑方柱的3维效应.由于风洞试验得到的干扰效应具有海量数据的特点,所以目前的研究主要集中在风荷载方面,而对于风压干扰的研究极少.
本文对一般性方形高层建筑模型,通过改变间距比以及施扰建筑和受扰建筑之间的高度比,进行测压风洞试验,详细分析施扰建筑对于测试模型表面局部风压的影响,得出了一些有普遍意义的结论.
1 试验简介
1.1 风洞及风场
试验在同济大学土木工程防灾国家重点实验室TJ-2风洞进行.TJ-2风洞为闭口回流式矩形接口风洞,试验段宽3m、高2.5m、长15m.采用被动模拟方法在TJ-2风洞模拟了我国《建筑结构荷载规范》(GB 50009—2001)中的C 类风场(风速剖面指数α=0.22),几何缩尺比为1∶400.试验风速为12m·s-1.由于我国规范未直接给出各类地貌紊流度剖面,故本次试验采用日本建筑荷载规范(AIJ 2004)[10]建议的紊流度公式.详细的平均风速剖面和紊流度剖面的模拟结果与理论值的比较见文献[11].
1.2 试验概况
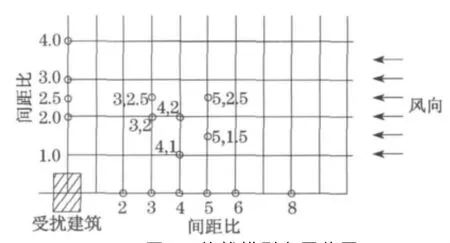
图1 施扰模型布置位置Fig.1 Arrangements of buildings and coordinate system
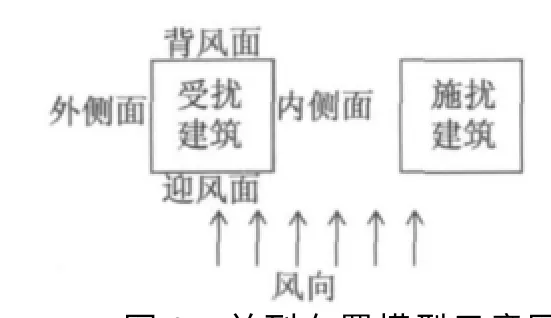
图2 并列布置模型示意图Fig.2 Schematic diagram of models in parallel arrangement
2 结果分析
2.1 试验数据处理方法
本文的风压系数定义与文献[12]相同

在分析干扰效应时,以平均风压系数和脉动风压系数定义的干扰因子为指标,其定义如下:
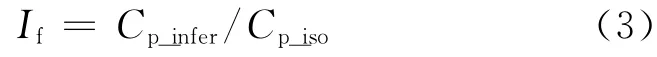
式中:Cp_infer为干扰状态下受扰建筑的风压系数,可以是平均风压系数或是脉动风压系数;Cp_iso为相对应的单体状态受扰建筑平均风压系数或是脉动风压系数.施扰建筑对受扰建筑的影响主要通过干扰因子If来体现,If>1表示增加,If<1表示减小,If=1表示施扰建筑没有影响.
在考虑施扰模型高度变化的影响时,定义高度比为

式中:H为施扰模型高度;h为受扰模型高度.
2.2 施扰位置变化的影响分析
在分析间距比变化对于受扰建筑表面风压的影响时,仅考虑两者等高的情况,也即高度比ηh=1.0.
2.2.1 平均风压系数
图3是受扰建筑4个面平均风压系数干扰因子等值线随间距比变化分布图.在图3a中,狭缝面干扰因子均自前侧(迎风棱边)向后侧逐渐减小,不同的是,间距比越小,该值自前向后减小的速度越快.这是因为并列布置时,2个建筑间形成了间隙流;间距比越小,气流通过狭缝的速度越快,从而产生较大的负压.其干扰因子最大值随间距比的增大而减小,在间距比等于2时取得最大值,位于大约(2/3)H高度处,数值为1.9;同时其最小值变化趋势相反,在间距比为4时达到最大值1.1,说明干扰作用随间距比增大而渐趋平均.图3b显示的是外侧面平均风压系数干扰因子变化图,和狭缝面不同,其均在后缘上端角部处取得最大值,这是因为施扰建筑的存在改变了单体状态时受扰建筑的流体形状,使得受扰建筑外侧面后端角部处旋涡脱落加剧,这在文献[9]中已经得到证实.相对侧风面,间距比的改变对于迎风面平均风压系数干扰因子的影响较小,在迎风面的大部分位置,平均风压系数干扰因子略有增大,仅在靠近外侧面的棱边处,干扰因子小于1.0,这在图3c中可以观察到.在图3d中,受扰建筑背风面平均风压系数干扰因子均超过1,也即施扰建筑存在时,受扰建筑背风面吸力增大,和迎风面相同,在所研究的间距比范围内,间距比改变对于其干扰因子数值变化的影响不大,干扰因子基本介于1.25~1.35之间,说明施扰建筑后的流体形态没有发生质的变化,这和文献[8-9]的研究结论是一致的,也即并列布置的2个建筑物间存在小于2的临界间距比,当间距比超过该临界值时,建筑后的流体形态由非对称流转变为对称流且在2 个建筑物后分别形成旋涡脱落,所以建筑物的背风面气动力特征趋于稳定.
综上所述,本文思考异形柱框轻和短肢剪力墙住宅结构体系的相关内容,发现短肢剪力墙是剪力墙结构的分支,在结构布置方面比较灵活,可调整性较强。如今建筑行业已经能够为人们提供高度舒适性的住宅,这其中离不开混凝土异形柱、短肢剪力墙的支持,二者使得高层住宅体系更加完善,不仅满足舒适性,还实现良好的节能效果,也让建筑住宅有良好的耐久性和安全性特点。

图3 受扰建筑平均风压系数干扰因子随间距比变化等值线图(0°风向角,ηh=1.0)Fig.3 Contours of mean pressure coefficient interference factors on each side of principal building at various spacing ratios at 0°wind direction(ηh=1.0)
2.2.2 脉动风压系数
图4是受扰建筑脉动风压系数干扰因子等值线随间距比变化分布图.在图4a中,脉动风压干扰因子沿狭缝面的变化趋势和平均风压干扰因子相同,均从前缘逐渐向后减小,其最大值主要位于狭缝面前缘上端角部和中间0.6H~0.8H高度范围内且随间距比的增大而减小,但整体干扰作用随间距比的增大而趋向于平均.在间距比等于2时,狭缝面干扰因子最大值等于2.2,位于前缘上端角部处,这是因为该部位处于流体加速分离的高流速区域,流体脉动加剧,所以此处较为危险.由图4b可以看出,和狭缝面不同,外侧面脉动风压系数干扰因子最大值主要位于后缘上端角部,但其值受间距比的影响较小,基本稳定在1.2左右.此外,由于间距比增大,通过受扰建筑两侧的气流趋向于对称,所以整个外侧面干扰因子大于1的范围随间距比的增大而整体略有增加.在图4c中,迎风面脉动风压系数干扰因子受间距比改变的影响较小,其值基本介于0.9~1.1之间,在间距比等于4时,整个迎风面干扰因子分布非常均匀,这说明间距比增大,施扰建筑对于受扰建筑的影响逐渐减小,又因为迎风面直接受来流作用,所以相对其他几个表面,其受施扰建筑的影响就更小.图4d为背风面脉动风压系数干扰因子,由图可知,数值大于1的干扰因子范围随间距比的增大而略有增大,且其最大值出现位置逐渐靠近背风面(2/3)H高度附近区域,当间距比等于4时,干扰因子在背风面大部分仍然大于1,这是由于施扰建筑的3维效应仍然存在,导致受扰建筑周围的湍流脉动增加,也就是说当间距比为4 时干扰效应还是比较显著的.

图4 受扰建筑脉动风压系数干扰因子随间距比变化等值线图(0°风向角,ηh=1.0)Fig.4 Contours of fluctuating pressure coefficient interference factors on each side of principal building at various spacing ratios at 0°wind direction(ηh=1.0)
2.3 施扰模型高度变化的影响分析
在分析高度比变化对于受扰建筑表面风压的影响时,根据文献[8-9]的结论,施扰建筑并列布置时存在小于2.0的临界间距比,当间距比大于该值时,受扰建筑的气动力特征变化趋于一致.通过对本文实验数据的分析也发现有此规律,所以在此仅考虑间距比为2.0的情况,其他间距比情况不再赘述.
2.3.1 平均风压系数
图5是受扰建筑平均风压系数干扰因子等值线随高度比变化分布图.在图5a中,狭缝面平均风压系数干扰因子最大值随高度比的增大而增大,其出现位置随高度比的增大而上升,由高度比等于0.7时的0.5H上升到高度比等于1.3时的前缘上端角部,且此时值最大,接近2.3.这是因为当施扰建筑高度变化时,由施扰建筑上部产生的分离流会作用到受扰建筑不同的高度,又结合狭缝产生的高速流,导致了局部较大的负压.相比之下,外侧面的干扰因子要小于狭缝面,这可以从图5b看出,干扰因子数值均大于1,也即施扰建筑的存在导致受扰建筑外侧面的吸力增大.其最大值均位于后缘上端角部处且随高度比的增大而增大,高度比等于1.3时,其值等于1.6.值得注意的是,在高度比等于0.7 时,外侧面0.7H处以下的干扰因子也相对较大,反映了高度比变化对于受扰建筑的影响效果.在图5c中,干扰因子均在1.0左右,且随高度比增大只有微弱增加,说明高度比变化对于受扰建筑迎风面平均风压系数干扰因子的影响较小.在图5d中,背风面平均风压系数干扰因子最大值主要位于远离施扰建筑一侧的上端角部处和中间部位且随高度比的增大而增大,但中间部位的干扰因子最大值位置下移,其原因为当施扰建筑高度大于受扰建筑高度时,其对受扰建筑后的漩涡有压制作用,导致背风面下部的漩涡增强,在高度比等于1.3时,平均风压系数干扰因子最大值等于1.4.综上可知,受扰建筑各个面干扰因子均随高度比的增大而增大,即相邻建筑物中较高的建筑物对较为低矮的建筑物有显著的干扰作用,这和文献[1]的研究结论是吻合的.
2.3.2 脉动风压系数

图5 受扰建筑平均风压系数干扰因子随高度比变化等值线图(0°风向角,间距比为2.0)Fig.5 Contours of mean pressure coefficient interference factors on each side of principal building at various height ratios at 0°wind direction(Y/B=2.0)

图6 受扰建筑脉动风压系数干扰因子随高度比变化等值线图(0°风向角,间距比为2.0)Fig.6 Contours of fluctuating pressure coefficient interference factors on each side of principal building at various height ratios at 0°wind direction(Y/B=2.0)
图6是受扰建筑脉动风压系数干扰因子等值线随高度比变化分布图.在图6a中,狭缝面干扰因子最大值随高度比的增大而增大且其位置随高度比的增大而上升,在高度比等于1.3 时,数值接近2.7,位于狭缝面前缘上端角部,总体上其变化趋势与平均风压一致,但干扰作用更为显著.这说明建筑物周围的特征湍流对于脉动风压增大有很大的影响.由图6b可以看出,外侧面的脉动风压系数干扰因子由前缘部分向后缘逐渐增大,其最大值出现在后缘上端角部处且随高度比的增大而增大,而前缘的干扰因子数值均小于1,也即脉动风压相对单体状态减小.在图6c中,与平均风压相似,迎风面脉动风压系数干扰因子较为稳定,但数值稍大,基本介于1.0~1.2 之间,其最大值均位于靠近内侧棱边的上端角部处且数值随高度比的增大而增大,最大为1.3.由图6d可知,随着高度比的增加,背风面脉动风压系数干扰因子增大且其最大值出现位置逐渐靠近背风面中下部,在高度比等于1.3时,其最大值为1.3左右,可见施扰建筑高度较大时,压制了受扰建筑上部的漩涡,导致其下部漩涡强度增大,从而脉动增加.
3 结论
本文以平均风压系数和脉动风压系数各自定义的干扰因子为研究对象,详细分析了0°风向角下,并列布置的2个方型建筑,施扰模型位置和高度变化对于受扰方柱表面平均和脉动风压的影响.由以上对试验结果的分析可以得出如下结论.
(1)高度比等于1.0,平均和脉动风压系数干扰因子最大值在狭缝面和外侧面均随间距比的增大而减小,但脉动风压受干扰影响较大,间距比等于2时,其干扰因子在狭缝面取得最大值2.2;迎风面和背风面干扰因子最大值受间距比改变的影响均较小,仅随间距比的增大而略有增大,但背风面的干扰因子相对迎风面大,其干扰因子最大值为1.4.
(2)间距比等于2.0,在建筑物狭缝面、外侧面和背风面,平均和脉动风压系数干扰因子均随高度比的增加而增大,其中狭缝面脉动风压放大最为明显,脉动风压系数干扰因子最大值达到2.7;背风面脉动干扰较弱,干扰因子为1.3左右.而在迎风面,干扰因子受高度比的影响很小.
(3)并列布置时,受扰建筑狭缝面风压改变较为显著,尤其是迎风前缘的上端角部处,平均风压和脉动风压均显著放大,所以当有临近建筑物时,需要注意相应部位的围护结构加固.
[1] Khanduri A C,Stathopoulos T,Bedard C.Wind-induced interference effects on buildings:a review of the stateof-the-art[J].Eng Struct,1998,20(7):617.
[2] Xie Z N,Gu M.Mean interference effects among tall buildings[J].Eng Struct,2004,26(9):11.
[3] Gu M,Xie Z N.Along-wind dynamic interference effects of tall buildings[J].Adv Struct Eng,2005,8,163.
[4] Xie Z N,Gu M.Simplified formulas for evaluation of windinduced interference effects among three tall buildings[J].J Wind Eng Ind Aerodyn,2007,95(1):31.
[5] Xie Z N,Gu M.Across-wind dynamic response of high-rise building under wind action with interference effects from one and two tall buildings[J].The Structural Design of Tall and Special Buildings,2009,18(1):37.
[6] Ajith Kumar R,Gowda B,Sohn C.Interference excitation of a square section cylinder[J].Journal of Mechanical Science and Technology,2008,22(3):599.
[7] Zhang A,Gu M.Wind tunnel tests and numerical simulations of wind pressures on buildings in staggered arrangement[J].J Wind Eng Ind Aerodyn,2008,96:2067.
[8] Wong P T Y,Ko N W M,Chiu A Y W.Flow characteristics around two parallel adjacent square cylinders of different sizes[J].J Wind Eng Ind Aerodyn,1995,54/55:263.
[9] 陈素琴,顾明,黄自萍.两并列方柱绕流相互干扰的数值研究[J].应用数学和力学,2000,21(2):131.CHEN Suqin,GU Ming, HUANG Ziping. Numerical computation of the flow around two square cylinders arranged side by side[J].Applied Mathematics and Mechanics,2000,21(2):131.
[10] Architectural Institute of Japan.AIJ 2004 Recommendations for loads on buildings[S].Tokyo:Architectured Institute of Japan,2004.
[11] 韩宁,顾明.两串列方柱局部脉动风压干扰研究:第1部分 迎风面效应[J].振动与冲击,2009,28(12):188.HAN Ning,GU Ming.Interference effects on local fluctuating pressure of two square tall buildings in tandem arrangement:part 1 windward side effects[J].Journal of Vibration and Shock,2009,28(12):188.
[12] Holmes John D.Wind loading of structures[M].2nd ed.London:Taylor and Francis,2007:199.

