标准C＊－代数间保持一类正元比较关系的映射

方小春，赵 冬，徐小明，2

（1.同济大学 数学系，上海200092；2.上海应用技术学院 理学院，上海201418）

1 结果陈述

假设H是一个复Hilbert空间，B（H）是H上所有有界线性算子构成的代数，F（H）是B（H）中所有有限秩算子构成的理想，F（H）＋是F（H）中所有正元构成的集合.任给算子T∈B（H），分别用T＊，R（T）表示T的伴随算子和值域.

设AH是B（H）的一个C＊－子代数，如果AH包含F（H）和单位元I，则称AH是H上的一个标准C＊－代数.将AH中所有正元构成的集合记作AH＋.

定义1［1，2］设A，B∈AH＋.若 存在X∈AH，使得

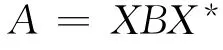
则记A≤B.

若A≤B且B≤A，则称A等价于B，此时记作

A≈B.

容易证明，≈是AH＋中的一个等价关系，它推广了Murray－von Neumann在C＊－代数中定义的投影等价关系.任给A∈AH＋，用〈A〉表示A在AH＋中关系≈的等价类.

定义2 设φ是AH＋上的一个映射.若φ具有可加性且对任给的λ∈R＋和A∈AH＋都满足φ（λA）＝λφ（A），则称φ是一个半线性映射.任给一个网｛Ai｝，如果｛Ai｝按弱算子拓扑收敛于A，那么φ（Ai）也按弱算子拓扑收敛于φ（A），则称φ是一个弱连续映射.

若映射φ：AH＋→AH＋满足对任给的A，B∈AH＋，如果A≤B，那么φ（A）≤φ（B），则称φ是一个保持比较关系≤的映射.若φ满足φ（A）≤φ（B）当且仅当A≤B，则称φ是一个双边保持比较关系≤的映射.近些年来，很多学者对算子保持问题做了很深入的研究［3－8］.本文讨论AH＋中比较关系≤的双边保持问题.

本文的主要结果如下.

定理1 设φ：AH＋→AH＋是一个弱连续半线性满射.如果存在可逆元M∈B（H），使得对任意的A∈AH＋，都有φ（A）＝MAM＊，则φ是一个双边保持比较关系≤的映射.

定理2 设φ：AH＋→AH＋是一个弱连续半线性满射.如果φ双边保持比较关系≤，则

（1）任给A，B∈AH＋，A≈B⇔φ（A）≈φ（B）.（2）任给A∈F（H）＋，rank（φ（A））＝rank（A）.根据定理1，很容易得到下述推论.

推论1 设φ：B（H）＋→B（H）＋是一个弱连续半线性满射.如果φ双边保持比较关系≤，则

（1）任给A，B∈B（H）＋，A≈B⇔φ（A）≈φ（B）.

（2）任给A∈F（H）＋，rank（φ（A））＝rank（A）.

2 定理的证明

定理1的证明 设A，B∈AH＋.如果A≤B，根据定义1，则存在X∈AH，使得A＝XBX＊.所以

因为MM＊＝φ（I）∈AH＋，MM＊在B（H）中可逆，所以（MM＊）－1∈AH＋.因为AH是由AH＋线性张成 的 且MAH＋M＊＝φ（AH＋）＝AH＋，所 以MXM＊∈AH，故MXM＊（MM＊）－1∈AH.根据定义1，有φ（A）≤φ（B）.

反之，设A，B∈AH＋.如果φ（A）≤φ（B），根据定义1，则存在X∈AH，使得φ（A）＝Xφ（B）X＊.所以

因为φ是AH＋上的满射，所以M－1AH＋M＊－1＝M－1φ（AH＋）M＊－1＝AH＋.故M－1XM＊－1∈AH.又因为M－1M＊－1＝M－1IM＊－1∈AH＋，所 以（M－1·M＊－1）－1∈AH＋.从而（M－1XM＊－1）（M－1M＊－1）－1∈AH.根据定义1，有A≤B.

为了证明定理2，首先给出几个引理.

引理1 设A，B∈AH＋且A≤B.若dimR（B）＜∞，则dimR（A）＜∞.

证明 不妨假设dimR（B）＝k＜∞.由于A≤B，根据定义1，则存在X∈AH，使得A＝XBX＊，故

dimR（A）≤dimR（B）＝k＜∞.

引理2 设A，B∈AH＋.若dimR（A）＜∞或dimR（B）＜∞，则A≤B当且仅当dimR（A）≤dimR（B）.

再证必要性.由于A≤B，根据定义1，存在X∈AH，使得A＝XBX＊，故dimR（A）≤dimR（B）.

引理2揭示了有限秩正算子的秩与比较关系≤之间的一些联系.根据引理2，得到如下推论.

推论2 设A∈AH＋.下列命题等价.

（1）dimR（A）＝k.

（2）任给X∈AH＋，若dimR（X）＝k，则A≈X.

（3）存在X∈AH＋，若dimR（X）＝k，则A≈X.

命题1 设φ：AH＋→AH＋是一个半线性满射.如果φ双边保持比较关系≤，则：

（1）任给A，B∈F（H）＋，A≈B⇔φ（A）≈φ（B）.

（2）任给A∈F（H）＋，rank（φ（A））＝rank（A）.

证明 （1）因为φ双边保持比较关系≤，所以对任给的A，B∈F（H）＋，A≤B⇔φ（A）≤φ（B）.容易验证对任给的A，B∈F（H）＋，A≈B⇔φ（A）≈φ（B）.

（2）只需证明（1）⇒（2）.设任给A，B∈F（H）＋，A≈B⇔φ（A）≈φ（B）.给定自然数k，将F（H）＋中所有k秩算子构成的集合记作Fk（H）＋.证明对任给的自然数k和A∈Fk（H）＋，rank（φ（A））＝rank（A）.

当k＝0时，只需证明φ（0）＝0.因为φ是半线性映射，所以φ（0）＝φ（0＋0）＝φ（0）＋φ（0）＝2φ（0），故φ（0）＝0.

假设对任给自然数k≤m和A∈Fk（H）＋，rank（φ（A））＝rank（A）.下面证明当A∈Fm＋1（H）＋时，rank（φ（A））＝rank（A）.用反证法，假设当A∈Fm＋1（H）＋时，rank（φ（A））≠m＋1，分两种情况来讨论：

1）若rank（φ（A））＜m＋1，即rank（φ（A））≤m，根据假设有rank（φ（φ（A）））＝rank（φ（A））.应用推论2，有φ（φ（A））≈φ（A）.故A≈φ（A）.根据推论2，m＋1＝rank（A）＝rank（φ（A））＜m＋1.显然，矛盾.

2）若rank（φ（A））＞m＋1，证明φ的像不包含m＋1秩算子.若k＜m＋1且B∈Fk（H）＋，根据假设，有rank（φ（B））＝rank（B）＜m＋1.若k＝m＋1且B∈Fk（H）＋，根据推论2，有B≈A.故φ（B）≈φ（A），从而rank（φ（B））＝rank（φ（A））＞m＋1.若k＞m＋1且B∈Fk（H）＋，则存在正交集合｛e1，…，ek｝（ei∈H，i＝1，…，k），使得且rank，应用k＝m＋1时的结论，有.因为φ是半线性映射，所以因 此 rank （φ（B））≥这样证明了φ的像不包含m＋1秩算子.这与φ是满射矛盾.

现在证明定理2.

定理2的证明

（1）因为φ双边保持比较关系≤，所以对任给的A，B∈AH＋，A≤B⇔φ（A）≤φ（B）.则容易验证对任给的A，B∈AH＋，A≈B⇔φ（A）≈φ（B）.

（2）因为φ是弱连续的，根据结论（1）和命题1及其证明过程，显然结论（2）成立.

［1］ Cuntz J.The structure of multiplication and addition in simpleC＊－algebras［J］.Math Scand，1977，40：215.

［2］ Cuntz J.Dimension functions on simpleC＊－algebras［J］.Math Ann，1978，233（2）：145.

［3］ Bell J，Sourour A R.Additive rank－one preserving mappings on triangular matrix algebras［J］.Linear Algebra Appl，2000，312（1／3）：13.

［4］ Clark S，Li C K，Mahle J，et al.Linear preservers of higher rank numerical ranges and radius［J］.Linear and Multilinear Algebra，2009，57（5）：503.

［5］ Dolinar G，Molnár L.Maps on quantum observables preserving the Gudder order［J］.Rep Math Phys，2007，60（1）：159.

［6］ Hou J C.Rank preserving linear maps on B（X）［J］.Sci in China（ser.A），1989，32（15）：929.

［7］ Li C K，Rodman L.Preservers of spectral radius，numerical radius，or spectral norm of the sum on non negative matrices［J］.Linear Algebra Appl，2009，430（7）：1739.

［8］ Zhang X L，Hou J C，He K.Maps preserving numerical radius and cross norms of operator products［J］.Linear and Multilinear Algebra，2009，57（5）：523.