燃料电池阴极空气过滤器对SO2 的化学吸附仿真

吕 洪，刘 湃，蔡书娟，马建新

（1.同济大学 汽车学院，上海201804；2.同济大学 新能源汽车工程中心，上海201804）

随着燃料电池技术的进步，质子交换膜燃料电池（PEMFC）将有可能替代传统的内燃机作为汽车的新一代发动机，从而减少化石燃料的消耗和环境污染.目前，燃料电池发动机（FCE）的耐久性是制约新能源汽车发展的关键问题之一.燃料电池的耐久性受使用环境空气品质的影响，特别是在交通拥挤的隧道以及污染严重的化工厂区，空气中有害气体会对燃料电池造成严重的损害，其中SO2对燃料电池的损害最大［1］.燃料电池发动机阴极空气过滤器是防止空气中有害气体对燃料电池发动机损害的最有效方法之一，它不仅要具备过滤颗粒物的功能，而且要具备过滤有害气体的功能；同时，还要满足气流阻力小，结构紧凑等要求.本文以开发设计高效过滤器为出发点，采用实验手段获取滤芯材料对SO2的吸附行为数据，建立过滤器化学吸附性能与进气属性的数学模型，并采用仿真手段对过滤器的吸附行为进行模拟，从而达到优化过滤器结构和预测过滤器寿命的目的.

1 实验与数学方法

1.1 实验

本实验采用KOH 改性的活性炭作为滤芯材料，分别分析了不同滤芯厚度、SO2初始进气体积分数和气体流速对吸附性能的影响.实验在常温下进行，将SO2标准气和空气的混合气体通入装有一定厚度改性颗粒活性炭的圆柱形反应器中，混合气经过反应器后进入质谱仪（MS），通过质谱仪记录得到活性炭吸附SO2的穿透曲线［2］.

1.2 数学方法

1.2.1 吸附模型

本文在传统吸附理论的基础上进行建模，通过采集上述实验数据，并参考相关的吸附等温式以及活性炭固定床吸附传质规律方程，利用Datafit软件建立数学模型，为仿真模拟提供参数.

（1）Wheeler公式是描述低穿透体积分数下吸附剂床层穿透曲线的床层吸附动力学理论方程，如公式（1）所示.

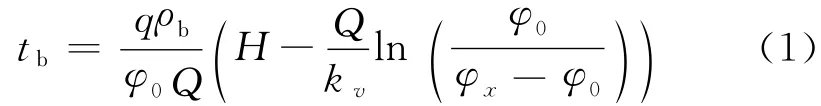
式中：tb为达到穿透时规定的气体体积分数φx对应的穿透时间；φ0 为初始气体体积分数；Q为空气流量；q为平衡吸附量；ρb 为活性炭堆密度；H为活性炭堆积厚度；kv为吸附速率常数；φx为穿透时规定的气体体积分数.

（2）Langmuir吸附等温式假设吸附剂表面对气体的吸附为单分子层吸附，相邻的被吸附分子之间没有作用力，吸附速度与固体表面空位数值成正比，且吸附平衡是动平衡，当吸附速度和解吸速度相等时，即达到吸附平衡［3］.如公式（2）所示.

式中：q为单位吸附容量；qm为平衡吸附量；k为吸附平衡常数；φ为气体体积分数.

（3）希洛夫方程是用于计算固定床穿透时间的近似方程式，描述了在一定实验条件下吸附剂厚度与保护作用时间关系的床层吸附动力学规律.如公式（3）所示.

式中：Tb为穿透时间；T0为保护作用时间损失；K为穿透时间系数；L为吸附层长度.

1.2.2 仿真数学模型

本文采用Fluent软件进行仿真，用户自定义函数（user define function，UDF）是用户自编的程序，它可以被动态地连接到Fluent求解器上来提高求解器性能，用户自定义函数用C 语言编写.

本文UDF 用于定义每个滤芯小单元的吸附SO2的饱和规律：每次迭代计算时，首先记录小单元吸附SO2的质量，并和实验测得的平衡吸附量进行比较，如果超过平衡吸附量，则该小单元不再发生化学吸附反应，计算流程如图1所示.

由此可见，必须通过一系列化学吸附实验建立平衡吸附量与初始气体体积分数以及空气流速之间的数学关系，以获得不同进气条件下的平衡吸附量参数，使用户自定义函数可以运行.仿真主要采用以下方程.

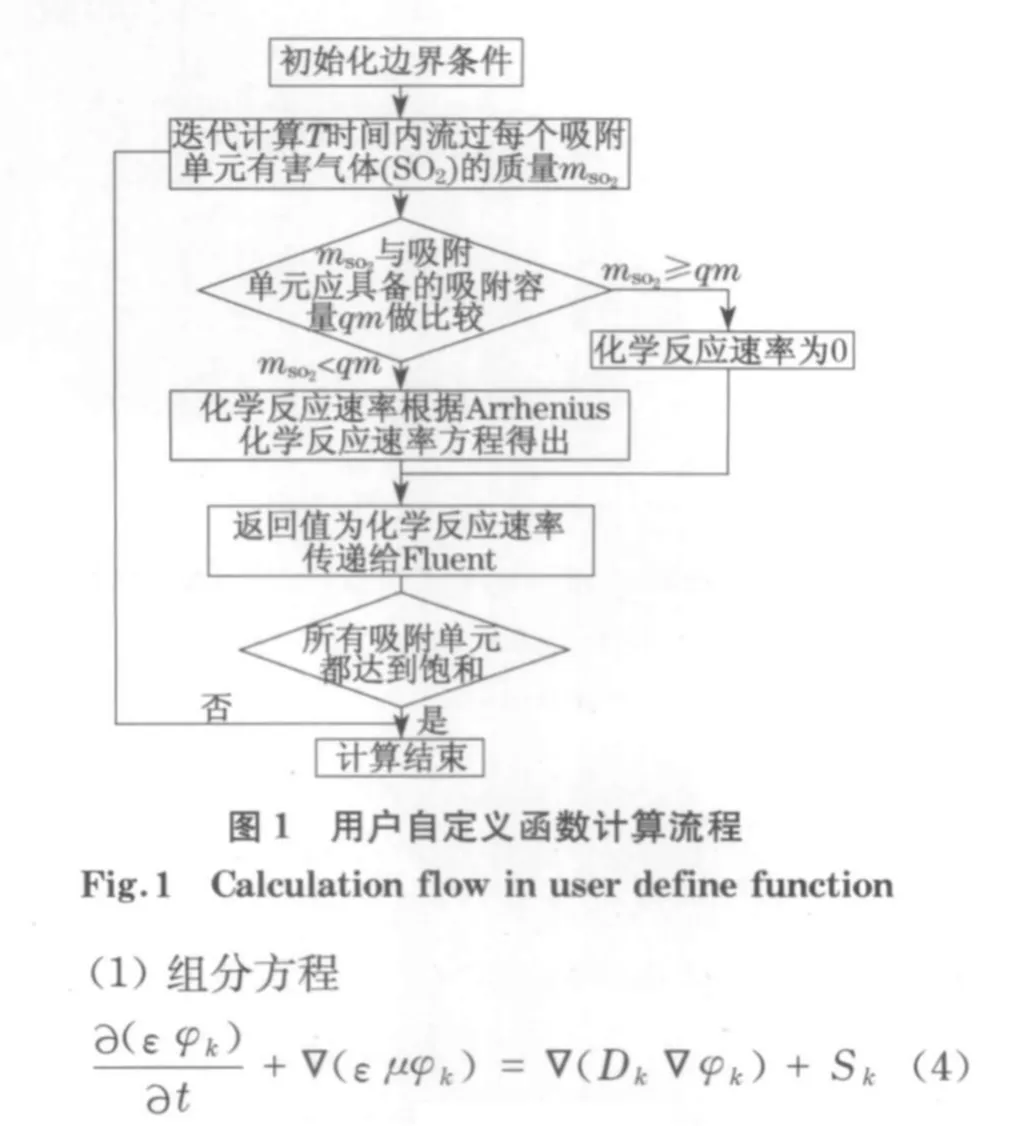
式中：ε，φk，μ，Dk，Sk分别表示孔隙率、组分体积分数、空气粘度、组分有效扩散系数和组分源项；下标k为组分代码.

（2）化学反应速率方程［4］

式中：kr为反应速率常数；k0为指前因子；Ea为实验活化能；R为气体常数；T为温度.

（3）约束条件方程

式中：mSO2为每个小单元吸附SO2的质量；q为滤芯的单位吸附量；m为小单元的质量.

2 结果与讨论

2.1 化学吸附实验与数学模型

2.1.1 进气属性与化学吸附性能的关系

在堆积厚度为40 mm，不同空气流速条件下（0.088～0.701m·s－1），分别通入5种不同初始体积分数（2～60）×10－6的二氧化硫和空气的混合气，实验结果如图2所示.在相同流速下，穿透时间随着SO2初始体积分数的增大而减小；在相同初始体积分数下，穿透时间随着空气流速的增大而减小.

本文以吸附实验为依据，采用Wheeler公式对实验数据进行拟合（将φ0 和Q作为变量，其余作为参数），拟合曲线与实验结果符合良好，如图2所示.

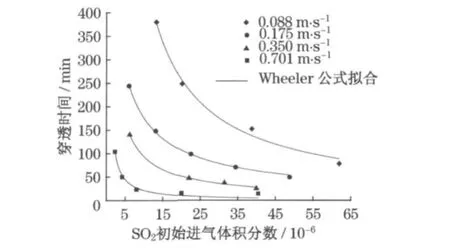
图2 穿透时间与SO2 初始进气体积分数的的关系Fig.2 Relation between breakthrough time and inlet concentration

Langmuir吸附等温式可以计算滤芯材料在不同进气属性下的穿透曲线，并对其积分计算得出平衡吸附量.因此，在上述模型的基础上，通过Datafit软件，采用Langmuir吸附等温式建立平衡吸附量－SO2初始进气体积分数－空气流速的三维模型，如图3所示.在不同的空气流速下，平衡吸附量qm均在11～12mg·g－1左右，Langmuir系数k在0.13～0.30内，拟合精度较高，而在相同的空气流速下，平衡吸附量则随着SO2初始进气体积分数的增加而增大，最后稳定在12 mg·g－1.与二维图相比，三维模型图可以计算出在一定范围内任意初始进气体积分数和空气流速所对应的平衡吸附量，模型具有连续性.通过此三维模型可以计算出在一定初始进气体积分数、空气流速范围内的平衡吸附量，作为编写UDF约束方程的依据，用于Fluent仿真计算.

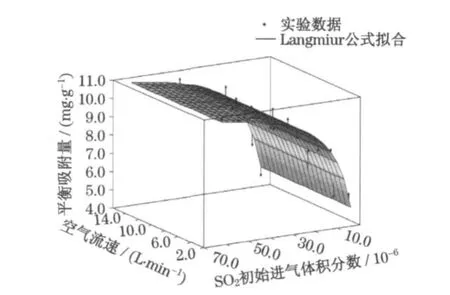
图3 平衡吸附量－SO2 初始进气体积分数－流速的三维模型图Fig.3 3D map among adsorption capacity－inlet concentration－air flow rate

2.1.2 滤芯厚度对吸附性能的影响

在SO2初始进气体积分数为15×10－6、空气流速为0.35m·s－1条件下，分别选定9种堆积厚度的活性炭进行吸附实验，图4 为不同堆积厚度下的穿透曲线.

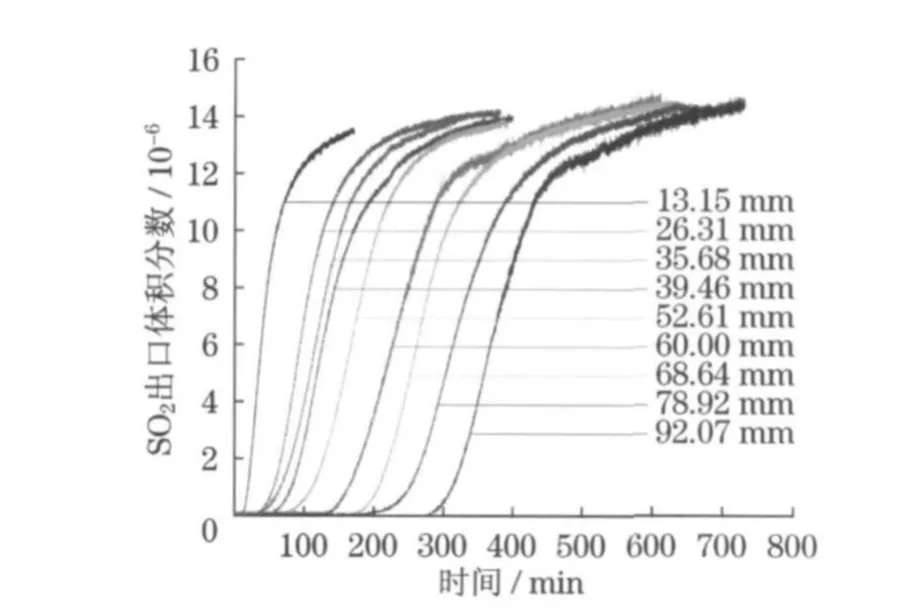
图4 不同堆积厚度下活性炭的穿透曲线Fig.4 Breakthrough curves under different thickness of adsorbent

由实验结果可知，随着活性炭堆积厚度的增加，其吸附SO2的穿透时间相应增加.这是由于在初始进气体积分数和空气流速相同的条件下，对同一种活性炭来讲，活性炭堆积厚度越大，对SO2的吸附容量越大，而且气体在活性炭表面停留时间更长，化学吸附更充分，导致穿透时间较长，而堆积厚度对活性炭的平衡吸附量没有明显影响，在本实验条件下，活性炭对SO2的平衡吸附量约为11mg·g－1.

本实验所得穿透时间与堆积厚度的关系如图5所示，由图5可知，前两个较小堆积厚度的数据点在“死区”范围内［5］，应该排除，通过对其余7个点利用希洛夫公式拟合，得到穿透时间t与堆积厚度h的关系函数为

t＝4.565（h－29.8） （7）

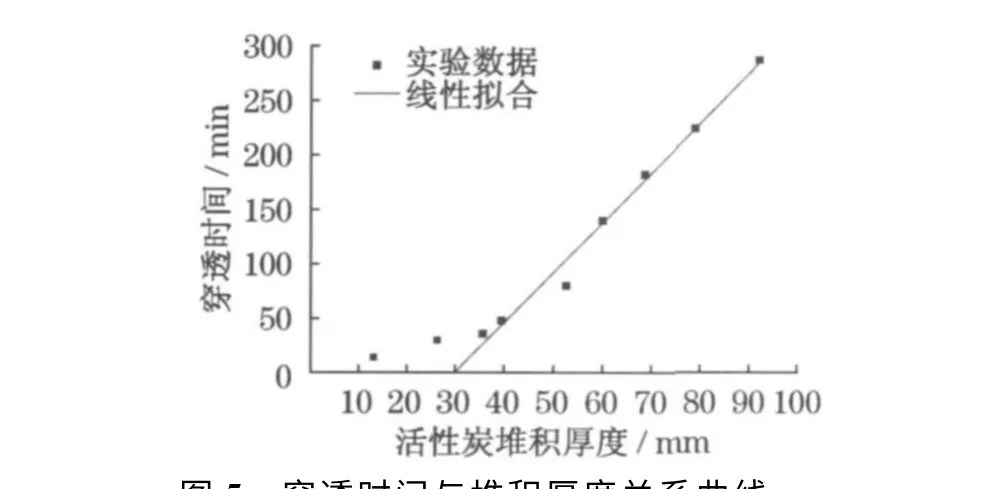
图5 穿透时间与堆积厚度关系曲线Fig.5 Relation between breakthrough time and thickness

通过本实验可知，堆积厚度与穿透时间近似成线性关系，其穿透时间系数为4.565，其含义是体积分数分布曲线在吸附层中移动单位长度所需要的时间；“死区”厚度为29.8mm，表示床层未被充分利用的长度.本实验确定了堆积厚度与吸附穿透时间之间的数学关系，为已经建立的吸附性能－进气属性数学模型的扩展提供了依据.

2.2 过滤器化学吸附行为的仿真

通过建立进气属性与化学吸附性能的数学模型，为过滤器的化学吸附仿真研究提供了基础.本文采用Fluent软件对图6所示结构的过滤器进行化学吸附的仿真，该过滤器针对5kW 的燃料电池发动机系统设计.为了减小运算量，本文对空气过滤器进行了适当简化，即只针对滤芯多孔介质反应区域进行模拟.多孔介质反应区域模型的主要尺寸和边界条件如图6和表1所示.

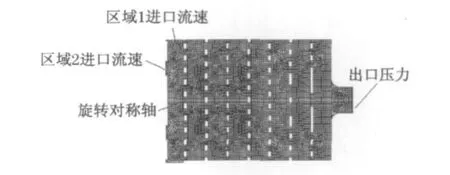
图6 Gambit导入Autocad后建立的网格以及边界条件示意图Fig.6 Schematic diagram of mesh and boundary condition

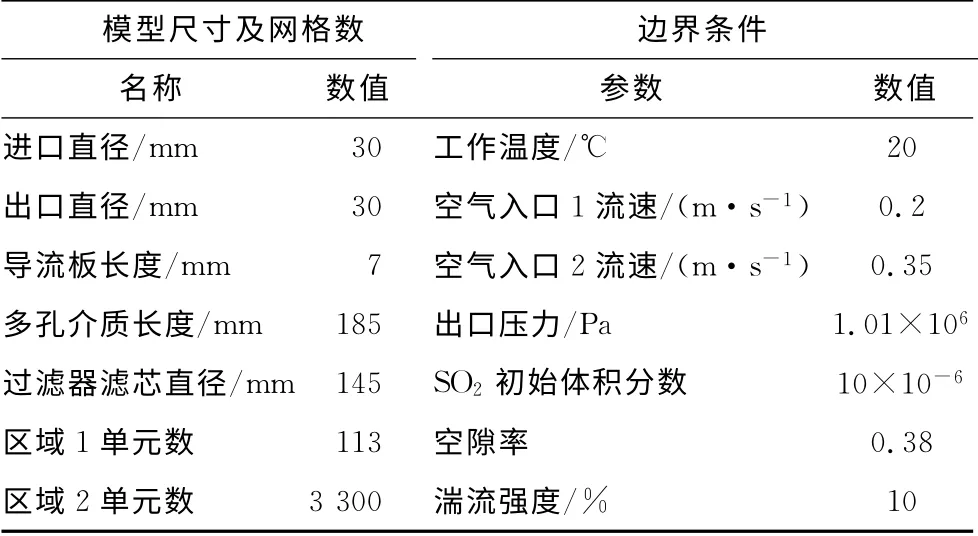
表1 边界条件主要参数表Tab.1 List of parameters for boundary condition

图7 5kW 燃料电池空气过滤器SO2 吸附量分布图Fig.7 Distribution of SO2capacity with time in air filter for 5kW fuel cell stacks

图7为过滤器的SO2吸附仿真结果，显示了SO2在过滤器内的化学吸附过程.含有SO2的空气经过滤器过滤后，出口的空气不含SO2，随着过滤时间的增加，过滤器内SO2吸附逐渐达到饱和，最后过滤器失效.通过过滤器的化学吸附仿真研究，可以清晰地显示SO2在过滤器内的分布，结果表明该结构的过滤器达到吸附饱和时担载SO2的容量分布比较均匀，基本没有“死区”、“短路”现象，充分利用了吸附材料.同时，通过仿真，预测该结构的过滤器使用寿命约1 203h.

3 结论

本文通过实验和计算机仿真相结合的方法研究了燃料电池发动机阴极空气过滤器SO2的化学吸附行为，建立了平衡吸附量－SO2初始进气体积分数－空气流速的三维数学模型，以及穿透时间与滤芯厚度的数学模型，为过滤器的化学吸附仿真提供相关参数；通过对5kW 燃料电池发动机空气过滤器的仿真，可以清晰地模拟出SO2在过滤器内的吸附行为，并预测过滤器的失效时间为1 203h，为过滤器结构设计和优化提供了理论依据和方法.

［1］ 杨代军.大气污染物对质子交换膜燃料电池性能影响的研究［D］.上海：华东理工大学资源与环境工程学院，2007.YANG Daijun.Study on effects of air pollutants on the performance of proton exchange membrane fuel cell［D］.Shanghai：East China University of Science and Technology.School of Resources and Environmental Engineering，2007.

［2］ MA Xiaowei，YANG Daijun，ZHOU Wei，et al.Evaluation of activated carbon adsorbent for fuel cell cathode air filt ration［J］.J Power Sources，2008，175（1）：383.

［3］ Mesquita M E，Vieira e Silva M.Preliminary study of ph effct in the application of Langmuir and Freundlich isotherms to Cu－Zn competitive adsorption［J］.Geoderma，2002，106（3－4）：219－234.

［4］ Kolaczkowski S T，Chao R，Awdry S.Application of a CFD code （Fluent）to formulate models of catalytic gas phase reactions in porous catalyst pellets［J］.Chemical Engineering Research and Design，2007，85（11）：1539.

［5］ 宣晓波.固定床活性炭脱硫穿透特性试验研究［D］.西安：西安交通大学能源与动力工程学院，2003.XUAN Xiaobo. Study of desulfurated breakthrough characteristic for active carbon in packed bed［D］.Xi’an：Xi’an Jiao Tong University.School of Energy and Power Engineering，2003.