机载捷联惯导的导航计算模型与精度分析

刘 春，周发根

（1.同济大学 测量与国土信息工程系，上海200092；2.现代工程测量国家测绘局重点实验室，上海200092）

惯性导航系统（inertial navigation system，INS）是20世纪初发展起来的一种自主式导航系统，其基本原理是根据牛顿提出的惯性空间的力学定律，利用陀螺仪和加速度计等惯性敏感元件来感知运载体的角速度和加速度信息，然后通过积分运算，得出导航参数以确定载体位置［1］.因此惯性导航系统是一种既不依赖于外部信息，又不发射能量的自主导航系统，具有极强的抗干扰能力，能够实时地提供十分完备的导航参数，除了能提供运载体的位置和速度外，还能给出高精度的姿态信息.

一个完整的惯性导航系统主要由惯性测量装置（inertial measurement unit，IMU）、导航计算机、控制显示器等3个部分组成.目前应用中的惯性导航系统主要分为两类：机械平台式惯性导航系统（gimbaled inertial navigation system，GINS）与捷联式惯性导航系统（strapdown inertial navigation system，SINS）.捷联式惯导系统没有实体平台，陀螺和加速度计直接固连在载体上，由计算机完成惯性平台的功能，因此有时也称作数学平台，其主要功能是坐标变换矩阵和姿态角的计算［2］.

由于采用数学平台代替了实体平台，捷联式系统具有结构简单、体积小、质量轻、成本低、初始对准快等优点.因此随着计算机技术和惯性传感器技术的发展，捷联式系统已经广泛应用于火箭、导弹、战斗机和其他飞行器上［3］.近年来，在民用领域，捷联式系统更是占据统治地位，在地下勘探、机器人技术、汽车导航等方面发挥了重要作用.捷联惯导与GPS构成的组合系统已广泛应用于地面移动测图、辅助航空摄影测量、航空遥感等领域.

捷联惯导系统在短时间内能提供高精度的导航参数，但随着导航时间的增长，误差积累很快.因此，大量学者致力于捷联导航算法的研究，并作出了重要贡献.其中最具代表性的是Paul G.Savage，他对捷联惯导的姿态更新、速度更新、位置更新等算法都做了深入研究，取得了杰出成果［4］.秦永元等人也对以增量形式输出测量值的捷联惯导系统，研究了误差补偿算法，对姿态解算的圆锥效应、速度解算的划桨效应、位置解算的涡卷效应，都给出了相应的补偿方法［1］.然而，与目前许多介绍惯导算法的参考文献一样，文献［1，4］都侧重捷联导航算法，没有给出实用的捷联导航计算模型.

文献［5］分析了捷联式惯导系统的动态误差特性，分别讨论了陀螺漂移、加速度计零偏、初始对准误差对捷联惯导系统的影响，具有重要的借鉴作用.然而在实际导航过程中，通常受到上述各种误差源的共同影响.因此本文在前人工作的基础上，设计了一套完整的捷联导航算法，使整个导航过程，从数据采集到最后输出完备的导航参数，得以清晰地实现.并利用机载GPS／SINS系统的实测数据进行导航计算，探讨实际导航过程中捷联惯导系统在各种误差源共同影响下的误差特性.采用卡尔曼滤波进行GPS／SINS松散组合解算，结合卡尔曼平滑，分析SINS在组合系统中的作用和精度情况.

1 捷联惯性导航系统的组成

捷联惯性导航系统没有实体平台，惯性敏感元件（陀螺和加速度计）直接安装在载体上，其敏感轴通常在载体坐标系的三轴方向上.陀螺仪测定载体相对于惯性参照系的运动角速度，并由此计算载体坐标系至导航坐标系的变换矩阵，通过此矩阵，把加速度计测得的加速度值变换到导航坐标系，然后进行积分运算，得到所需要的导航定位参数，同时，利用坐标变换矩阵提取姿态信息［1］.

1.1 捷联惯导坐标转换关系

坐标系统在惯性导航定位中具有重要的地位，具体的导航计算都是在一定的坐标系统中进行的.图1给出了惯性导航系统中常用的坐标系统.

从图1中可以看出，捷联惯导系统中常涉及到5类不同的坐标系，分别为地心惯性系（i系）、地固系（e系）、当地水平坐标系（L 系）、游移方位坐标系（w系）、载体坐标系（b系）.值得注意的是，L 系和w 系的原点一般选在载体质心，而图中将L 系和w 系的原点选在地球表面，是为了更清楚地反映它们的三轴指向.以上5类坐标系之间可以通过相应的旋转矩阵进行转换，它们之间的转换关系可以参阅文献［2］，这里不再列出.

图1 捷联惯导系统中的坐标系Fig.1 Coordinate system of strapdown inertial navigation system

1.2 数据采集

在捷联惯性导航系统中，IMU 直接固联在运载体上，陀螺和加速度计分别测量载体的角运动信息和线运动信息，结果以二进制文件输出，供后期处理.

IMU 的输出内容包含了采样时刻、载体沿3个轴向的角速度、沿3 个轴向的比力，环境温度等信息，见表1.为了减小误差，有的IMU 以角度增量和速度增量形式输出.

受惯性器件本身性能和外界环境的影响，IMU的输出值通常都含有误差，需要进行补偿.一般来说，在惯导系统工作之前要对IMU 的各项误差进行检校测定，并加以补偿.实际过程中，IMU 的输出数据可能出现断裂等异常情况，需要对测量值进行内插和重采样.

表1 IMU 测量数据Tab.1 IMU measured data

值得一提的是，所有的测量值都是沿IMU 本身3个轴线方向的.由于IMU 本身的轴线定义与载体坐标系不能完全一致，因此要将IMU 的输出值转换到载体坐标系中.加速度计无法测量重力，其输出值是沿IMU轴线的每单位质量所受到的非惯性力，通常称为比力［1］.在后续的导航计算中，要进行重力补偿.

2 捷联惯性导航系统计算模型

2.1 导航方程

导航方程的推导基于牛顿第二定律和哥氏定理，在不同的导航坐标系中有不同的表现形式.对于工作在非极区的捷联惯导系统，为了简化计算，导航坐标系一般选取当地水平坐标系.这样，捷联惯导系统完全等效于指北方位的平台系统［1］.

选取L系作为导航坐标系时，取位置向量为rL，速度向量为vL.

式中：φ，λ，h分别为纬度、经度、大地高；ve，vn，vu分别为东向、北向、天向的速度.矢量形式的导航方程如下所示：

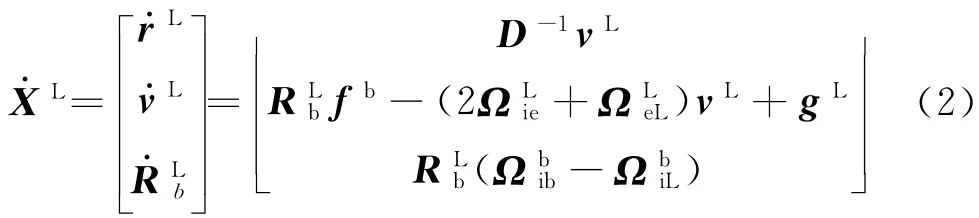
式中：

M，N分别为子午圈半径和卯酉圈半径为b系到L系的旋转矩阵；fb为比力观测值；Ωie，ΩeL，ΩiL分别为ωie，ωeL，ωiL的三维分量构成的反对称阵，其中ωie为地球自转角速度，ωeL为导航坐标系相对于地球的转移速率，ωiL为导航坐标系相对于惯性系的旋转角速度为角速度观测值.

2.2 导航计算

实践中为了避免高纬度地区数值计算的不稳定性，导航计算是在游移方位坐标系中（w 系）进行的［6］，然后将得到的导航参数再变换到L系.

图2给出了捷联惯性导航系统的计算流程图.从图中可以看出，导航计算的内容主要包括：姿态计算、比力分解、导航处理.首先根据上一时刻的姿态信息，利用陀螺的输出值，计算本时刻的姿态矩阵Rnb，称为姿态更新或者旋转矩阵更新，这个过程中涉及到地球自转角速度和导航坐标系的转移速率；接着利用旋转矩阵将比力观测值分解到导航坐标系中，并进行哥氏修正和重力补偿；最后积分求取速度和位置，并获取载体的姿态信息.下面给出w 系导航计算的关键步骤和主要公式.

图2 捷联惯导系统的导航计算模型Fig.2 Navigation calculation model for strapdown inertial navigation system

2.2.1 旋转矩阵更新

2.2.2 加速度计算

（1）哥氏加速度的计算哥氏改正项为

（2）正常重力的计算

重力补偿量gw应根据重力场模型来计算.对于WGS84椭球，可采用下面的公式：

（3）比力分解

将 比 力fb分 解 到w 系

2.2.3 速度计算

移动车体沿着轨道行走的过程中，导向机构的导向轮与轨道之间的作用关系均包含三个阶段：1)导向轮全部夹着直线轨道；2)导向轮部分夹着直线轨道，部分夹着弯曲轨道；3)导向轮全部夹着弯曲轨道，如图5。当转向架处于过弯状态时，弹簧被压缩或者拉伸，使得导向轮能够时刻压紧轨道并且避免卡死。阶段1情况下可以很容易看出导向轮与轨道之间均始终保持压紧状态，弹簧形变量保持不变，所以阶段1属于稳定行驶阶段。通过几何法对阶段2和阶段3情况下导向轮和轨道之间的接触关系进行分析。

2.2.4 位置坐标计算

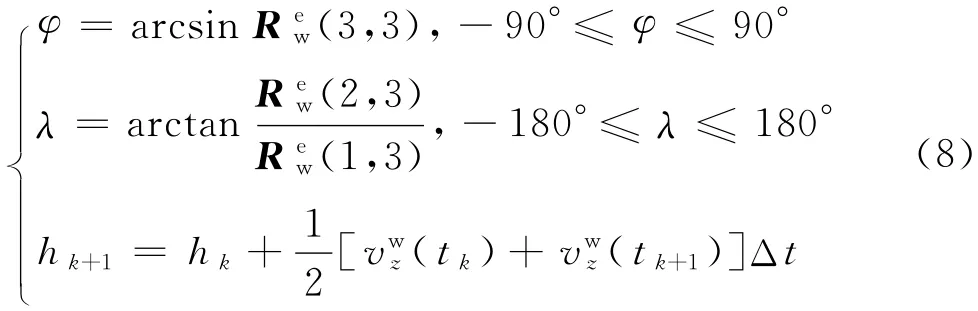
式中：vz为高度方向的速度分量的表达式中含游移方位角α，计算公式为

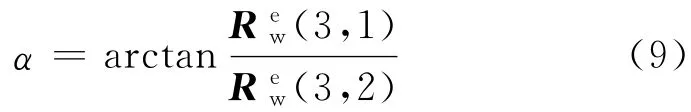
2.2.5 地速计算

游移方位坐标系中的速度vw需分解到当地水平坐标系中

2.2.6 姿态角提取

式如下：

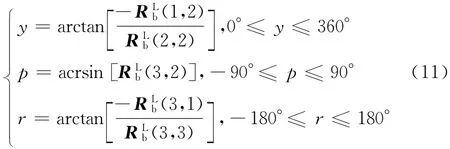
在实际导航应用中，常出现y趋于90°或者r趋于90°的情况，这时采用上式计算将会出现“奇点”，不但精度受影响，而且计算不安全.对此，文献［2］提供了更好的计算方法.以上计算过程中涉及到的公式及具体变量可以参阅文献［1，6－7］.

3 解算实例

3.1 数据来源

3.2 处理流程及结果

首先使用差分处理软件进行GPS 动态差分定位处理，可以达到厘米级的定位精度.然后以GPS差分定位结果作为标准，分析SINS的误差特性和精度情况，实验分以下两类.

（1）为了分析SINS的误差特性，将实验数据人为地删掉了长达10min的GPS信号.删掉GPS信号的时段内，SINS独立进行导航计算.以GPS定位结果为标准，衡量SINS导航计算结果的误差情况.表2列出了SINS在10min内的坐标和距离误差漂移情况，图3和图4给出了误差情况的直观表达.

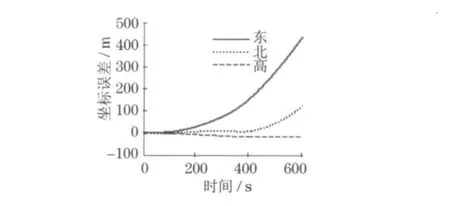
图3 SINS独立导航计算的坐标漂移Fig.3 Coordinate drift of SINS

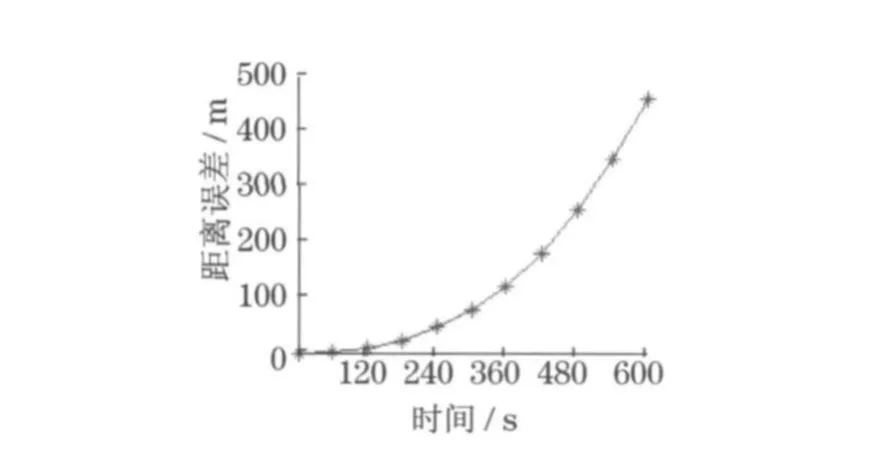
图4 SINS独立导航计算的距离漂移Fig.4 Distance drift of SINS

（2）为了分析SINS在组合系统中的作用和精度情况，共4 次人为删掉GPS 信号，每次删除的时长为1min.采用卡尔曼滤波进行差分GPS／SINS松散组合解算，并对组合结果进行卡尔曼平滑.图5给出了两段轨迹，其中一段为正常情况下GPS差分定位结果表示的飞行轨迹，另一段是人为删除GPS信号后GPS／SINS 松散组合定位结果表示的飞行轨迹.图6输出的是以GPS差分定位结果为标准衡量的GPS／SINS组合系统误差情况.

值得说明的是，考虑到图5 的重点是清晰表达出GPS信号失锁时段两个轨迹的差异，因此输出的仅仅是飞行过程中10min内的轨迹，删除GPS信号的时间为第1，4，7，10min.实际上，在GPS信号连续跟踪时，两条轨迹几乎重合，因此没必要将2h的飞行轨迹全部画出.另外，由于该图只是直观表达两轨迹的差异，并不反映具体的坐标信息，因此为了清晰起见，两条轨迹均以每6s一个点输出，实验证明，这样的输出间隔使得图形表达效果最清晰.

图5 部分实验飞行轨迹Fig.5 Part of experimental flight path

基于同样的考虑，图6中输出的仅仅是10min内的误差情况.然而不同的是，该图能定量反映误差情况，因此严格按照GPS的频率每秒一个点输出.

数据处理过程中，卡尔曼滤波方程取15阶误差向量Xk＝［δr，δv，ε，d，b］T作为状态.其中δr为位置误差；δv为速度误差；ε为姿态误差；d为陀螺漂移，考虑成一阶马尔科夫过程；b为加速度计偏置，也考虑成一阶马尔科夫过程.取SINS 与GPS 独立解算的坐标差值作为滤波器的部分输入［2］.

卡尔曼平滑采用的是双向滤波再平滑的固定区间平滑方式，可以参阅文献［2，7－8］.

图6 GPS／SINS组合导航计算的坐标误差Fig.6 Coordinate error of GPS／SINS integrated navigation

3.3 精度分析

从表2可以看出，当SINS独立导航计算时，误差增长很快，10min之后距离误差达到了400m 以上.从图3可以看出，坐标误差以抛物线形式的平滑曲线呈非线性增长.其中，高度通道的坐标误差最小，且变化平缓，是因为其误差仅受高度方向的速度误差影响，而高度方向的速度误差主要是由正常重力计算误差引起的，这个值相对较小.东向和北向的误差随时间推移增长越来越快，其中东向最显著，其原因是东向坐标误差同时受到东、北、高度3个方向的速度误差影响，且东向误差无反馈.但值得说明的是，这3个方向的速度误差影响并不一定是同向的，因此短时间内东向坐标误差增长最快并非必然，从表2中可以看出，在2s以内，东向和北向误差在数值量级上很接近.

表2 SINS独立导航计算的坐标漂移和距离漂移Tab.2 Coordinate drift and distance drift of SINS

从图4可以发现，距离误差增长与坐标误差情况很相似，结合表2可以看到，1min内距离误差在2m 以内，5min达到约80m，10min后误差则超过400m，这种变化趋势呈抛物线形状，而且是极其平滑的曲线.

图5中的两段轨迹显示，当GPS 信号良好时，GPS定位结果与GPS／SINS组合系统的定位结果几乎一致，这时SINS的作用主要表现为数据内插，解决GPS输出频率低的问题，当然，SINS的另一作用是输出高精度的姿态参数.当GPS 信号失锁时，组合系统的定位结果开始偏离GPS轨迹，当GPS信号重新锁定后，组合系统的轨迹又保持与GPS 一致.然而整个过程中，组合系统的轨迹始终是平滑的，没有出现突变的情况，这说明卡尔曼平滑是有效的，特别在GPS 失锁时段，卡尔曼平滑对于提高GPS／SINS组合导航结果的精度具有重要作用［2］，也体现出SINS能显著提高组合系统的完整性和抗干扰性.

图6定量地表示了GPS／SINS组合系统的误差情况.从图中可以看出，当GPS信号良好时，组合系统的误差很小；在GPS信号4 次失锁的时段内，出现了相似的误差情况，都呈抛物线增长，且误差最大值点近似出现在GPS信号失锁时段的中央，东、北、高度3个通道的误差均小于±0.3m，说明GPS信号失锁的短时间内，SINS仍能提供高精度的定位参数，充分体现了SINS的可靠性和抗干扰性.

4 结语

捷联惯性导航系统因其独特的优势，在军事和民用领域得到越来越广泛的应用，如何提高精度，一直是惯性技术界孜孜追求的目标.本文在介绍捷联导航算法之后，通过实测数据的计算与分析，得出SINS的坐标误差和距离误差累计均呈抛物线形式增长，10min内距离误差达到400 m 以上的结论.SINS在短时间内能提供高精度的导航参数.实验结果表明，SINS与GPS的组合系统，不仅能提供丰富的导航信息，更能解决GPS输出频率低、信号易受干扰、动态可靠性差等问题，具有很好的应用价值.

［1］ 秦永元.惯性导航［M］.北京：科学出版社，2006.QIN Yongyuan.Inertial navigation ［M］.Beijing：Science Press，2006.

［2］ 孙红星.差分GPS／INS组合定位定姿及其在MMS 中的应用［D］.武汉：武汉大学遥感信息工程学院，2004.SUN Hongxing.DGPS／INS integrated position and attitude determination and its application in MMS［D］.Wuhan：Wuhan University.School of Remote Sensing and Information Engineering，2004.

［3］ 许江宁，朱涛，卞鸿巍.惯性传感技术发展与展望［J］.海军工程大学学报，2007，19（3）：1.XU Jiangning，ZHU Tao，BIAN Hongwei.Development and prospects of inertial sensor technology［J］.Journal of Naval University of Engineering，2007，19（3）：1.

［4］ Paul G Savage.Strapdown inertial navigation integration algorithm design ［J］.Journal of Guidance，Control，and Dynamics，1998，21（1）：208.

［5］ 孙丽，秦永元，朱启举.捷联式惯导系统动态误差分析［J］.弹箭与制导学报，2007，27（4）：13.SUN Li，QIN Yongyuan，ZHU Qiju.Analysis on the dynamic error of strapdown inertial navigation system［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（4）：13.

［6］ 董绪荣，张守信，华仲春.GPS／INS 组合导航定位及其应用［M］.长沙：国防科技大学出版，1998.DONG Xurong，ZHANG Shouxin，HUA Zhongchun.GPS／INS integrated navigation and application［M］.Changsha：National University of Defense and Technology Press，1998.

［7］ 袁信，俞济样，陈哲.导航系统［M］.北京：航空工业出版社，1993.YUAN Xin，YU Jixiang，CHEN Zhe.Navigation system［M］.Beijing：Aviation Industry Press，1993.

［8］ 秦永元，张洪诫，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，1998.QIN Yongyuan，ZHANG Hongjie，WANG Shuhua.Kalman filtering and integrated navigation theory［M］.Xi’an：Northwest Industrial University Press，1998.