城市复合交通系统容量超级网络评估方法

谢 辉，于晓华，晏克非

（1.同济大学 交通运输工程学院，上海201804；2.上海市城市综合交通规划研究所，上海200040）

随着城市化进程加快，许多城市已进入交通快速发展时期.把握城市交通网络系统容量是实现城市交通发展与城市发展相协调的关键.网络容量问题的研究起始于20个世纪五六十年代，发展至今存在4种网络容量评估方法：①最大流最小截集方法［1］.将道路网抽象为图论中带有起点和终点的网络，分离各起点至终点间的所有截集中最小断面的通行能力，网络容量为各起点、终点间最小断面通行能力的简单加合.②线性规划模型［2］.求解以路网流最大化为目标函数，以总流量守恒为约束条件的路网最大流极值模型，得到的最大路网流为网络容量.③时空消耗法［3－4］.将城市路网想象成具有时空属性的一个容器，根据这个容器总的时空量和出行者出行所消耗的时空量，确定出整个路网的容量.④交通分配法［5－6］.将起讫点（OD）需求量采用增量分配的方法逐步分配到路网上，当有路段达到饱和或给定服务水平时，删除或割断该路段，当网络被分成两部分时，所删除或割断的路段的累加流量即为该网络的容量.

随着研究的深入，上述4 类网络容量评估方法考虑的因素越来越多，然而，这些方法均是基于城市路网容量的成果.在道路交通和轨道交通组合而成的复合交通体系下，由于存在各种单一方式和组合方式出行，各出行模式间相互影响，相互协助，需要构建不同的网络容量评估方法.

本文从城市复合交通系统中出行模式多样化的特点出发，将复合交通系统转化为由小汽车网络、公交网络和轨道交通网络有机组合而成的超级网络，复合交通系统出行成本转化为超级网络节点和线段成本之和.在现有需求出行结构不变，新增需求服从多项logit模型，出行路径选择行为服从wardrop均衡的假设前提下，建立了复合交通系统容量的超级网络分析方法与评估模型，其中上层为复合交通系统服务最大化问题，为从政府管理部门角度做出最大化网络储备容量的决策，下层为复合交通系统优化问题，为从出行者角度做出网络最小化出行成本的决策.

1 超级网络构建及其出行成本分析

城市复合交通系统可视为由小汽车网络、公交网络和轨道交通网络等3网络组成，出行者可选择3网络中1 种出行，也可以选择3 网络组合出行.为此，通过构建虚拟节点和换乘线段，将复合交通系统转化为由小汽车网络、公交网络和轨道交通网络有机组合的超级网络.这种方法称为复合交通系统的超级网络分析法.超级网络分析法中复合交通系统节点区域结构示意图如图1所示.

1.1 超级网络构建

图1 超级网络分析法中复合交通系统节点区域结构示意图Fig.1 Composite transportation system node regional structure in Super network analysis

1.2 出行成本分析

1.2.1 复合交通系统节点区域成本

根据图1显示，由小汽车网络、轨道交通网络和公交网络有机组合而成的复合交通系统节点区域共包括12条换乘线段、6个虚拟节点和1个起迄点.

线段1为小汽车线段i换乘到小汽车线段j的换乘线段，之间换乘线段成本为零.

线段2为小汽车线段i换乘到轨道交通网络的线段j的换乘线段，之间存在至换乘停车场的时间和停车费用以及步行至轨道车站的时间和等候轨道交通时间等换乘成本.

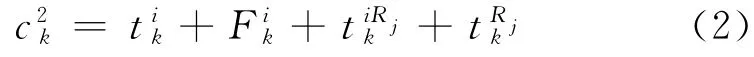
线段3为轨道交通线段i换乘到轨道交通线段j的换乘线段，之间存在停留等候时间和步行

至换乘线段j的步行时间等换乘成本.

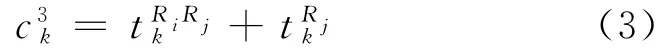
线段4为轨道交通网络的线段i换乘到公交网络中的公交线段j的换乘线段，之间存在步行至公交线段j的步行时间和等候公交线段j的候车时间等换乘成本.

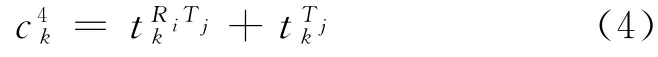
线段5为公交网络线段i换乘到轨道交通网络中的轨道线段j的换乘线段，之间存在步行至轨道车站的步行时间和等候轨道交通线段j的候车时间等换乘成本.

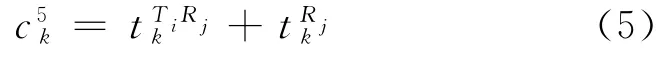
线段6为公交网络的公交线段i换乘到公交网络的线段j的换乘线段，之间存在停留等候时间和步行至换乘线段j的步行时间等换乘成本.

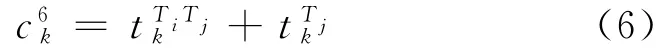
线段7为小汽车方式到终点s的停车线段，之间存在至停车场的时间、停车费用与步行至终点s的步行时间等成本.

线段8与线段9为轨道交通站点和公交站点至终点s的步行线段，之间存在步行时间或成本.

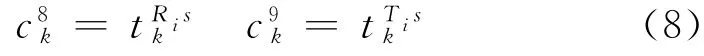
线段10为起点r到停车场取车线段，之间存在步行时间成本

线段11和线段12分别为起点r到轨道交通车站和公交车站的步行线段，之间存在步行至各站点的时间和候车时间等成本.

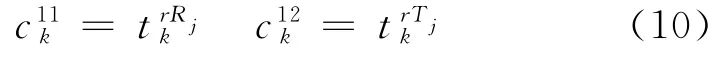
1.2.2 复合交通系统线段运行成本

复合交通系统线段a的运行成本为ta具有以下几种情况：

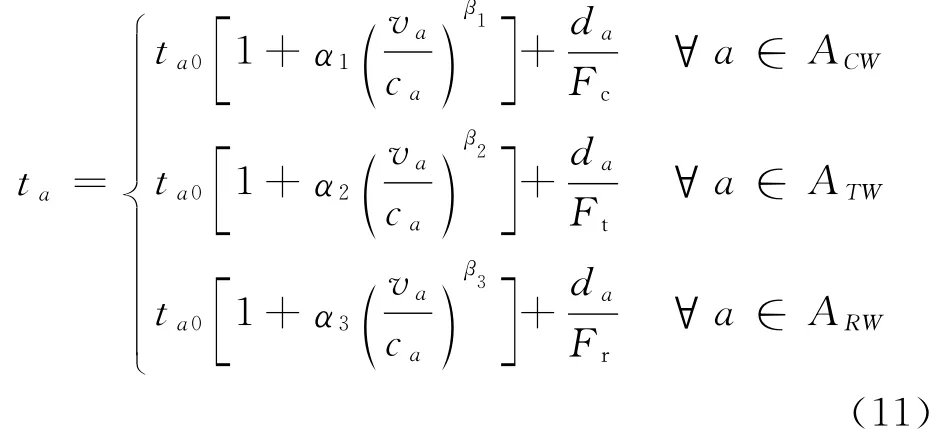
式中：ta0为复合交通系统上的自由流时间；ca，va为路段a的通行能力与流量；da为线段a的距离；ACW，ATW，ARW分别为小汽车网络、公交网络、轨道网络线段集合；αi，βi为BPR函数参数分别为道路网络、公交网络、轨道网络的单位距离运行费用.

2 复合交通系统容量评估模型

2.1 模型假设

为方便分析城市复合交通系统容量和建立相关分析模型，做出如下假设：①在新增出行者对出行目的地的选择服从多项logit模型.②出行者完全掌握路况信息，以用户均衡的方式选择出行路径.此外，为确保网络交通流的稳定性，考虑道路路段的通行能力约束.

2.2 模型构建

根据上述的假设，城市复合交通系统容量的超级网络评估模型如下.

上层：最大化流量问题（MRC）.

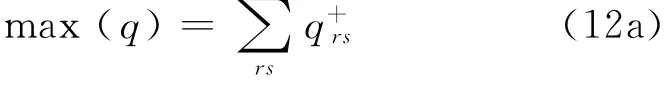
约束条件：

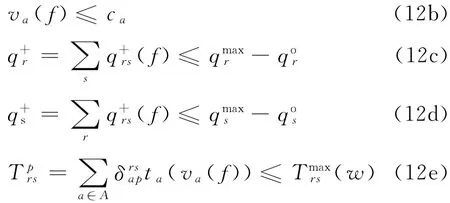
目标函数（12a）为网络储备容量最大化，式（12b）为路段通行能力约束，式（12c）和式（12d）为区域开发极限，式（12e）为服务水平要求，式（12f）为外部环境约束，式（12g）为非负条件.

其中f，va和满足用户均衡条件，即满足如下出行分布和均衡分配的组合模型.

下层：超级网络优化问题（CTN）.

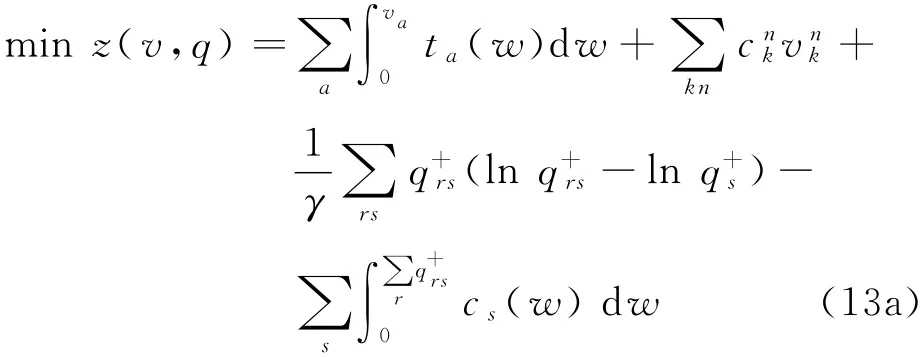
约束条件：

（1）流量守恒

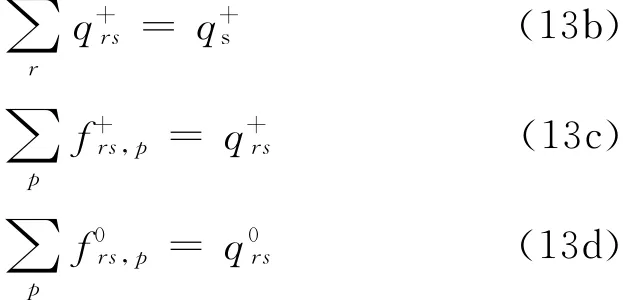
（2）线段与线段流量关系

（3）非负约束条件

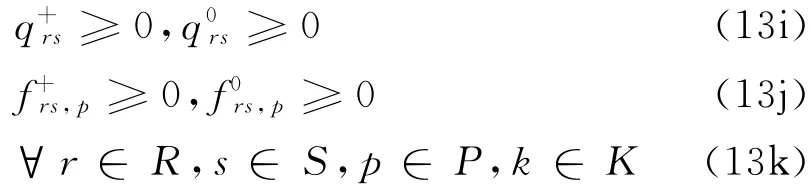
目标函数式（13a）由4项组成，第1项为著名的Beckmann变换，没有直观的经济意义，它们等价于出行路径选择满足Wardrop用户均衡；第2项为复合交通系统节点区域的总出行成本；第3项为出行目的地选择的熵函数，由此可以导出目的地选择服从logit 均衡；第4 项为出行者目的地选择的Beckmann变换（被选择了目的地的出行效应要大于或等于没有被选择的目的地出行效应）.

该模型具有很明显的特点：将复合交通系统视为超级网络，考虑了网络设施的规划者（政府管理部门）和使用者（出行者）间的相互影响，符合城市交通网络规划进程.在网络规划阶段，政府管理部门根据网络的运行效率等进行适当决策，而网络使用者在既有的网络设施上，利用出行路径的选择，同时进行出行方式、换乘节点的选择，简化了网络结构和网络容量模型结构.

3 模型求解

由上可知，城市复合交通系统容量超级网络分析评估模型是一个非线形双层规划模型，其下层为非线形的用户均衡网络分配模型，上层为最大流问题，虽然其目标函数为线形，但带有非线形的约束条件.对于非线性双层规划模型求解，一般是设计相应启发式算法，分别求解上、下层模型，然后，反复迭代上、下层模型的结果，直至收敛.具体步骤如下.

第1步：设定初始解.

第2步：下层CTN 模型求解.

第3步：非线形约束线形化.

将非线形约束式线性化，即将上层MRC模型线形逼近为标准型线性规划问题.

第4步：上层MRC模型求解.

采用标准的单纯形法求解MRC 模型的线性逼近后的标准型线性规划模型.求得

第5步：收敛性检验.

否则，令n＝n＋1，转入第2步继续迭代，直到满足收敛性或达到最大迭代次数时结束.

4 芜湖市城市交通网络系统容量分析

4.1 芜湖市城市交通网络描述

远期芜湖市中心城区规划了由道路网络和轨道交通网络组成的复合交通系统［7－8］.

其中，道路网总体格局为“三环＋格网”的形式.三环为联系组团中心的客运快速环（九华北路—弋江路）、组团间客货交通兼过境客运的快速环（扁担河东路）、中心城区外围的货运及过境交通的快速环（东环）.格网为增加东西向和南北向干路，构成芜湖中心城区各组团之间连贯的网格状干路系统和有机整体，促进城市走廊的健康发展.

远期规划轨道线段2条，共41.5km.布设16个轨道交通车站和4个P＋R（停车换乘）站点，如图2所示.

图2 芜湖中心城区复合交通系统结构示意图Fig.2 Complex traffic system structure diagram in Wuhu City

4.2 容量计算

论文利用MATLAB 优化工具箱和TransCAD交通软件平台进行仿真分析.

首先利用TransCAD 强大的GIS功能进行输入数据处理，以行列式形式（MATLAB 格式）输出.其次利用MATLAB超强大的函数工具箱拟合模型中各需求参数，编写模型求解程序，对城市交通网络系统容量模型进行求解计算.最后利用TransCAD 的GIS功能对MATLAB 程序计算的结果（路段流量和网络容量）进行可视化显示.

4.2.1 复合交通系统构建

构建芜湖市城市复合交通系统，图3 为复合交通系统典型节点（轨道站点16）网络化示意图.轨道站点16 为轨道线段二的终点站，2 000m 范围内服务5个起讫点，并包括1个P＋R 停车换乘场所.

图3 复合交通系统典型节点网络化示意图Fig.3 Compound traffic system network typical node diagram

4.2.2 数据输入

其容量模型输入的主要数据被分为两类：网络属性数据和需求数据.其中网络属性包括起终点分布及其质心确定、道路网络路段、P＋R 停车设施、轨道线网线段等.需求数据包括起讫点间的极限开发量、现状出行结构，以及一些基本假设设置（表1）.

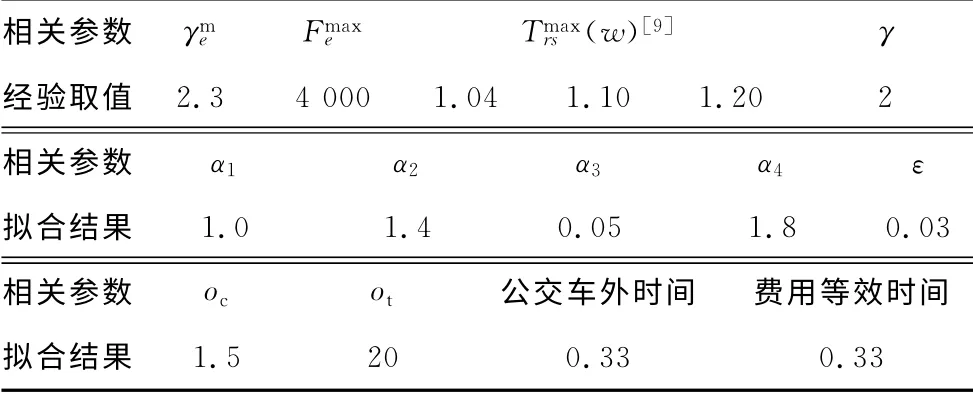
表1 模型的相关参数Tab.1 The related parameters in the model

4.3 计算结果及其分析

在不同网络服务水平（w）条件下，计算得到的网络容量结果不同.在高（w＝1.04）、中（w＝1.10）、低（w＝1.20）等级服务水平时，网络还可提供的总出行分别为586 780，706 315，799 725 人次·h－1，具体各组团间的网络容量情况如表2～4 所示，表中，C为城中组团；N 为城北组团；E 为城东组团；S为城南组团；W 为三山组团.

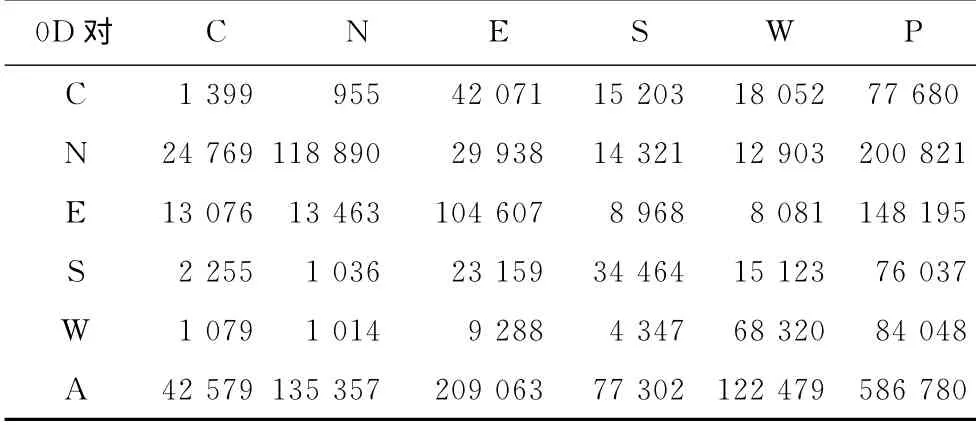
表2 网络储备容量计算结果（高服务水平）Tab.2 Network reserve capacity calculation results（w＝1.04） 人次·h－1

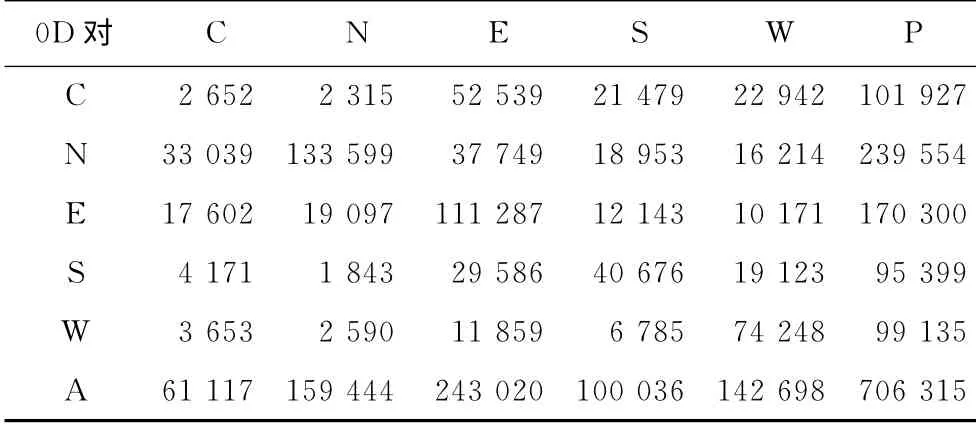
表3 网络储备容量计算结果（中服务水平）Tab.3 Network reserve capacity calculation results（w＝1.10） 人次·h－1

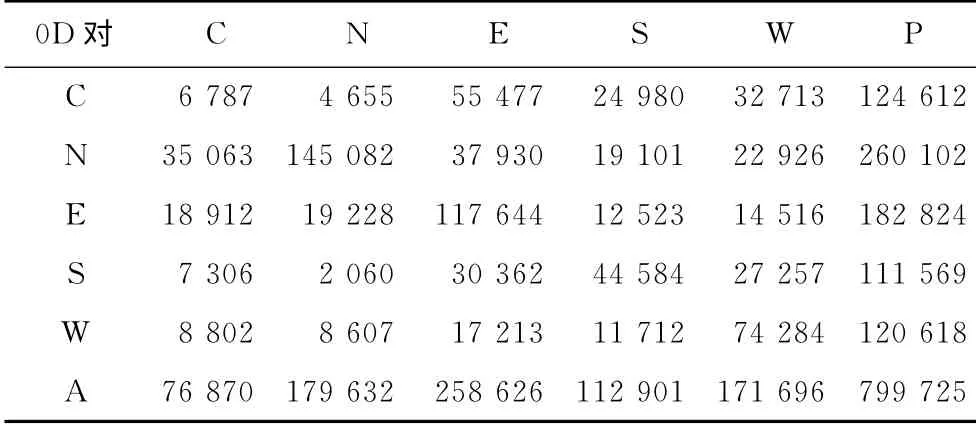
表4 网络储备容量计算结果（低服务水平）Tab.4 Network reserve capacity calculation results（w＝1.20） 人次·h－1

根据表2～4新增容量计算结果可得：

（1）规划网络能为城东组团（E）提供的服务最大，在高、中、低服务水平下，能为城东组团分别提供357 258，413 320和441 450人次·h－1的服务；其次是城北组团（N）和三山组团（W）；由于城中组团（C）道路网络等级较低，新增道路较小，采取了交通需求管理措施，所能提供的服务最小，高、中、低服务水平下分别为120 259，162 044和201 482人次·h－1.由此可见，该规划网络与城市向东向南发展策略一致，大力发展城东组团、城北组团和三山组团，使城市发展成“三叶”状.

（2）到达和离开各个组团的需求量各不相同，如在高服务水平下，城东组团（E）到达209 063 人次.h－1，离开为148 195人次.h－1，一方面是因为在高峰时期，网络流量本身不均衡；另一方面也说明该网络为城东组团提供的服务不同，可根据此服务不同，协调城东组团的新开发用地性质.

5 结语

从城市复合交通系统中出行模式多样化的特点出发，将复合交通系统转化为由小汽车网络、公交网络和轨道交通网络有机组合而成的超级网络，出行者利用出行路径的选择，同时进行出行方式、换乘节点的选择，简化了网络结构和网络容量模型结构.建立了复合交通系统容量的超级网络分析方法与评估模型，其中上层为复合交通系统服务最大化问题，下层为出行者角度做出网络最小化出行成本的决策.以芜湖市城市交通网络系统容量计算为例，案例结果显示该模型和算法的正确性和有效性.

［1］ Park M. Capacity modeling for multimodal freight transportation networks ［D ］. Irvine： University of California，2007.

［2］ 黄海军.运量分布与运量配流组合模型的研究［J］.系统工程理论方法应用，1995（3）：79.HANG Haijun.Research on combined trip distribution and traffic assignment models［J］.Systems Engineering Theory.Methodology ＆Applications，1995（3）：79.

［3］ WANG Danyi.Methods for analysis of passenger trip performance in a complex networked transportation system［D］.Fairfax：George Mason University，2007.

［4］ 黄海军.运量分布与运量配流组合模型的研究［D］.北京：北京航空航天大学经济管理学院，1992.HANG Haijun.Research on combined trip distribution and traffic assignment models［D］.Beijing：Beihang University.College of Management，1992.

［5］ Pierre Arnold，Dominique Peeters，Isabelle Thomas.Modelling a rail／road intermodal transportation system［J］.Transportation Research Part E：Logistics and Transportation Review，2004，40（3）：255.

［6］ 史峰，李志纯.网络扩容和拥挤道路使用收费的组合模型及求解算法［J］.中国公路学报，2003，16（2）：90.SHI Feng，LI Zhichun.Combined model and algorithm of expanding network capacity and road pricing［J］.China Journal of Highway and DTransport，2003，16（2）：90.

［7］ 同济大学交通运输工程学院.芜湖市世行贷款项目可研阶段——交通模型设计与预测［R］.上海：同济大学交通运输工程学院，2009.College of Transportation Engineering of Tongji University.The transport modeling of Word Bank Loan Project Research in Wuhu［R］.Shanghai：College of Transportation Engineering of Tongji University，2009.

［8］ 谢辉，周海容，晏克非.区域性交通项目建设的投资规模与效应分析——以芜湖市世行贷款项目三环路建设为例［R／OL］.［2009－10－11］.http：∥www.paper.edu.cn／index.php／default／releasepaper／cpmtent／20100－777.XIE Hui，ZHOU Hairong，YAN Kefei.The investment scale and effects of regional transportation project construction—with an example of the third－ring road of Word Bank Loan in Wuhu［R／OL］.Sciencepaper Online.http：∥www.paper.edu.cn／index.php／default／releasepaper／cpmtent／20100－777.

［9］ 同济大学交通运输工程学院.城市客运交通方式间资源配置优化技术［R］.上海：同济大学交通运输工程学院，2010.College of Transportation Engineering of Tongji University.The optimization technology of resource allocation in city passenger traffic modes［R］.Shanghai：Tongji University.College of Transportation Engineering，2010.