煤的可磨性指数测定精确度分析

谢卫宁 何亚群，3 左蔚然 周国平 吴仁超

（1.中国矿业大学化工学院，江苏省徐州市，221116；2.煤炭加工与高效洁净利用教育部重点实验室，江苏省徐州市，221116；3.中国矿业大学现代分析与计算中心，江苏省徐州市，221116）

煤的可磨性指数测定精确度分析

谢卫宁1，2何亚群1，2，3左蔚然1，2周国平1，2吴仁超1，2

（1.中国矿业大学化工学院，江苏省徐州市，221116；2.煤炭加工与高效洁净利用教育部重点实验室，江苏省徐州市，221116；3.中国矿业大学现代分析与计算中心，江苏省徐州市，221116）

在可磨性指数（HGI）测定回路中嵌入能耗测定模块，并对磨后细粒产品进行激光粒度分析。结果表明，研磨能耗与HGI不呈严格的线性相关关系；磨后产品的粒度分布与比表面积增加规律超出了可磨性指数测定依据面积假说所能解释的范畴。这导致煤的可磨性指数测定结果存在一定偏差。

煤炭 可磨性指数 激光粒度分析 比表面积 能量损耗

1932年美国人哈德格罗夫提出评价煤和一些脆性物料被磨碎难易程度的指标——哈氏可磨性指数（HGI）。该指数被广泛应用在指导工业磨破设备的选型。该测定方法基本依据是研磨煤粉所消耗的功与新产生的表面积成正比，其机械破碎方式主要为研磨破碎。然而，对比现代工业生产中所使用的大型研磨系统，无论在磨后产品的粒度范围、所依托的能耗假说还是在研磨机理上均存在差异性，使该指数的指导作用受到影响。可磨性指数测定所依据的面积假说，其产品临界粒度为0.074mm，而磨后产物中－0.074mm含量普遍超过10%，即存在一定的细磨及超细磨现象，超出了面积假说所能解释的范畴。此外，细磨和超细磨过程中特殊的力学特性和能耗规律会对矿物可磨性指数的测定产生一定的影响。

本文采用在HGI实验回路中嵌入能耗测定模块的方法，通过激光粒度分析仪分析磨后－0.074mm产品的粒度特征，并在荷兰学者R·T·胡基（R.T.Hukky）研究及昆明理工大学段希祥教授的细磨、超细磨下的能耗规律基础上，对当前HGI测定精确度进行分析。

1 煤样可磨性指数（HGI）测定

将12份实验煤样干燥后，采用逐级破碎的方法，不断调节破碎机的辊间距使其只能破碎较大的颗粒。破碎产品全部通过孔径1.25mm的筛子后，截取1.25～0.63mm之间的物料，并保证出样率大于45%。

将准确称重的50g煤样放入哈氏可磨性实验仪研磨，其中施加在钢球上的总作用力为284N，驱动电动机进行研磨，旋转60转。将磨得的煤粉用孔径为0.074mm的筛子在振筛机上筛分，并称量筛上和筛下的煤粉量，计算实验误差，并利用可磨性指数的经验公式计算煤样的可磨性，可磨性经验公式：

式中：HGI——煤样的可磨性指数；

M——研磨后的筛下物质量，g。根据经验公式计算的12份煤样的可磨性指数见表1。

表1 可磨性指数（HGI）数据表

2 磨后产品的粒度分布及研磨能耗测定

由于经验公式中仅仅要求磨后－0.074mm的质量含量而对其粒度分布没有明确要求，而颗粒的粒度特性将会对可磨性指数的精确性产生影响。因此，为获得磨后细粒级产品的粒度分布特征，利用贝克曼LS100型激光粒度分析仪对磨后－0.074 mm产品进行粒度测定，其粒度分布统一选用体积基准表示。1～5号煤样破碎产品的激光粒度分布见图1。

由图1可知，细粒级别在破碎产物中占据一定的比例：－0.074mm的平均含量为15.47%，－0.038mm含量为10.44%。分析其原因在于煤样在钢球的研磨作用下主要以表面粉碎为主，颗粒的表面不断被剥落而形成微粉成分，导致磨后产物中具有一定含量的微细颗粒。这表明煤样在哈氏可磨性指数测定仪中的破碎不仅有细磨过程，还存在着一定的超细磨现象。

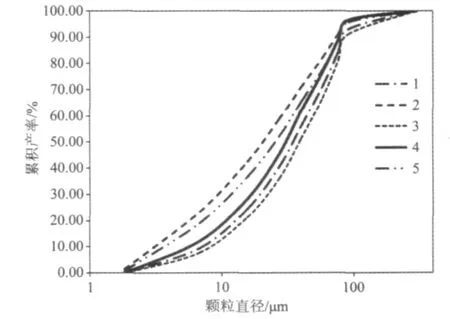
图1 1～5号煤样破碎产品的激光粒度分布

根据不同的矿物可磨性测定原理，可将可磨性测试分为两类。一类是在一定物料粒度范围和体积的前提下，测量在得到相同含量的小于某筛孔时所消耗的能量，邦德可磨性测定即基于此原理；另一类是在相同的物料粒度范围、质量和能量输入的条件下，测量研磨后小于某筛孔的含量多少，哈氏可磨性指数测定实验是基于此原理。但是对后者而言，由于在测试过程中，不同被测物料间存在一定的研磨阻力差异，这导致在同样旋转60转的情况下，由于所需克服的摩擦阻力的差异而导致能量输入的差异。本实验在可磨性指数实验回路中，嵌入了功耗模块。此模块能够精确测定研磨过程中的功率，此功率是扣除了磨机传动系统的功率、使钢球运动的功率及主轴承摩擦的功率，即发生磨矿作用的有用功率。磨机磨矿状态下测出的功率减去之前的空载功率，即获得发生磨矿过程的有用功率。可磨性指数与研磨功率关系图见图2。

图2 HGI与破碎功率关系图

图2表明，随着HGI的增加研磨功率先是呈现缓慢增加，在HGI为68.23的情况下达到最大，之后功率急剧下降，HGI为75.21时最小。与传统观点“HGI越大，表示煤的可磨性越好，煤越容易被磨碎”不同，HGI与研磨能耗不成严格的线性关系。分析原因在于HGI测定标准是以0.074mm为界划分，只要求测定－0.074mm含量，但并未明确－0.074mm以下的粒度组成。由上述激光粒度分析可知实验中－0.074mm的含量在15%～18%之间，其－0.038mm的含量超过10%，说明HGI测定过程中细磨及超细磨现象明显存在，此部分颗粒已经超出了面积假说能够解释的范畴。此外面积假说的推导将岩矿机械强度视为一个常数，而这是违反客观实际的。资料表明，0.15mm矿粒的机械强度为15mm矿块的2倍，粒度再变细时细粒的机械强度还将增大。而矿物颗粒减小至目标粒度时需要反复地研磨，在粒度减小过程中，颗粒的机械强度逐渐增大，所需能耗将会逐渐增加。

3 比表面积增加规律

比表面积是指单位质量多孔固体所具有的总表面积（包括外表面积和内表面积），其单位为m2／g。在哈氏可磨性指数测定仪中，煤样在钢球的反复研磨和剥削作用下粒度逐渐变小，输入的能量转化为颗粒增加的表面能和热能。按照破碎功耗中面积假说的观点，研磨所消耗的能量与新生成的表面积成正比。而在经验公式（1）的推导过程中，采用0.074mm作为整个－0.074mm比表面积的代表粒径。由前述激光粒度分析可知，－0.074mm含量超过15%，－0.038mm的含量更是超过10%，而此部分粒级的比表面积是0.074mm所不能够代表的。加拿大英属哥伦比亚大学S·萨主埃（S.Sadrai）等学者借助表面分析仪、扫描电镜、3D表面成像等技术，研究破碎产品各粒级的比表面积变化关系。各粒级比表面积及所占比例见表2。

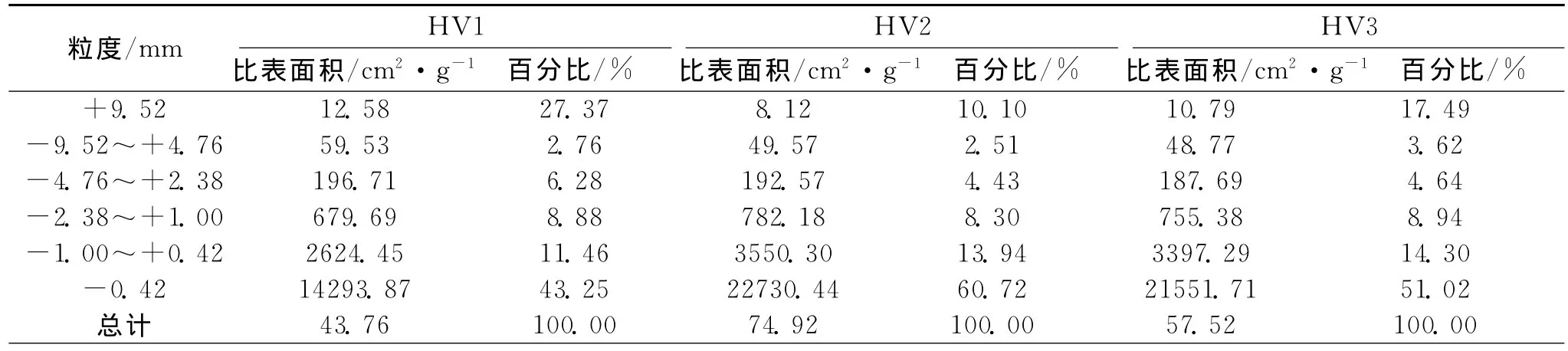
表2 各粒级比表面积大小及百分含量

由表2看出，随着颗粒粒度的减小，比表面积急剧增长，而将近一半的新生表面积由极细颗粒产生，因此选用0.074mm作为－0.074mm比表面积的代表粒径，其计算值要远小于实际值。

4 细磨及超细磨下的能耗假说

由前述分析可知，在可磨性指数测定过程中存在一定的细磨及超细磨现象，而该指数的测定依据为面积假说。对于破碎过程中的能耗学说，目前选矿界公认并经常使用的通常是三种：体积假说、裂缝假说和面积假说。芬兰学者R·T·胡基仿照工业办法对三种功耗假说进行验证分析：用每段破碎比为10的几段连续破碎，同时测出净功耗，并用15000～150000倍电子显微镜测定产物粒度下限，实验结果如图3所示。图中斜率分别为m＝0、m＝－0.5、m＝－1的3条虚直线依次表示按体积学说、裂缝学说及面积学说中粒度与功耗的关系曲线，而实线则为实测功耗曲线。三种学说所对应的产物界限分别为50mm，0.5mm和0.074mm。而对于产物粒度在0.074～0.038mm的细磨和－0.038mm的超细磨而言，采用3种学说所计算能耗偏低。因此面积假说将不能很好地解释可磨性指数测定过程中的能耗规律。

图3 破碎产物粒度与比功耗的关系

昆明理工大学段希祥教授在R·T·胡基功耗曲线基础上，推论细磨及超细磨下直线方程的斜率

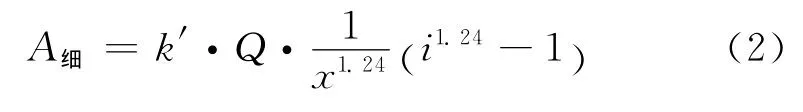
式中：A细——在细磨和超细磨情况下破碎单位质量矿物的能量消耗，kW·h／t；

k′——按有用功计的比功耗；

Q——煤炭处理量，t／h；

x——给矿粒度，mm；

i——破碎比。

此公式表明功耗的增长不是与新生表面积成正比，而是功耗增长大于新生表面积的增加。因此，面积假说不能够涵盖整个可磨性指数测定过程中的能量消耗规律，其计算能耗要小于实际能耗。面积假说将不足以作为可磨性指数的测定依据而需要加以修订。

5 经验公式的讨论

可磨性指数的测定原理是破碎定律，即根据磨碎所消耗的能量与被磨细粒增加的表面积成正比，表示如下：

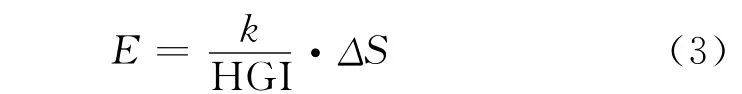
式中：E——磨碎物料时所消耗的有效能；

k——常数，与其它的能量消耗有关；

ΔS——物料研磨后增加的表面积。

在由公式（3）向公式（1）的推导中，进行了两点假设：

（1）假设磨碎过程中颗粒密度不变，单位质量下不同粒度的表面积（S）和粒度（d）存在关系：

（2）煤样磨碎筛分后，筛下物颗粒的直径为恰好通过筛子的孔径。

通过对两点假设的分析可知：在计算研磨过程中新生表面积增加量时，选择0.074mm作为计算－0.074mm筛下物的表面积代表粒径，而S·萨主埃（S.Sadrai）等学者的研究表明筛下物的表面积量要远大于计算中的选取值；同时能耗规律分析表明，研磨功耗的增长要大于新生表面积的增加，同时颗粒的机械强度随着粒度的减小而增加，从而导致研磨过程所消耗的能量大幅提升，这些超出了面积学说所解释的范畴。

6 结论

研磨过程中新增表面积量和研磨能耗是影响可磨性指数（HGI）的两大要素。而在经验公式推导过程中，选用0.074mm作为细粒级别产品表面积的代表粒径，其计算比表面积增加量远小于实际值；而测定依据——面积假说不能很好地解释超细粒级别的能耗规律，其测算值将小于实际值。由于两个因素的不确定性，导致可磨性指数测定中的不准确性。同时由于其研磨机理与工业磨机的差异，细磨及超细磨矿设备的迅猛发展等，使HGI在工业生产中的指导意义受到影响。

[1] 段希祥.细磨及超细磨下的功耗规律研究[J].有色金属（选矿部分）.1993（1）

[2] 张妮妮.煤的可磨性指数变化及破碎机理研究[D].浙江，浙江大学.2006

[3] A.J.林奇.破矿和磨矿回路[M].澳大利亚：原子能出版社，1983

[4] 谢广元等.选矿学[M].徐州：中国矿业大学出版社，2001的绝对值大于1。他采用数学推导的方法，在实验的基础上推导出细磨及超细磨下的能耗关系式为：

The precision analysis of Hardgrove Grindability Index of coal

Xie Weining1，2，He Yaqun1，2，3，Zuo Weiran1，2，Zhou Guoping1，2，Wu Renchao1，2

（1.School of Chemical Engineering and Technology，China University of Mining＆Technology，Xuzhou，Jiangsu 221116，China；2.Key Laboratory of Coal Processing and Efficient Utilization，China University of Mining＆Technology，Xuzhou，Jiangsu 221008，China；3.Advanced Analysis ＆Computation Center，China University of Mining ＆Technology，Xuzhou，Jiangsu 221116，China）

The energy consumption model was put into the measuring circuit of HGI to measure consumption，and the particle size of grinding product was measured by the laser particle size analyzer.the experimental result shows that the grinding energy don＇t have the liner correlation with the HGI，The characteristic of size distribution and the increase of special surface area are beyond the category which the HGI can explain based on the area hypothesis.It causes the deviation of the result of HGI of coal.

coal，HGI，laser particle size analysis，special surface area，energy consumption

TQ531.1

A

谢卫宁（1987－），男，河北衡水人，中国矿业大学在读研究生，主要研究方向矿物加工及电厂磨机研磨过程的研究。

（责任编辑 张毅玲）