基于滑动窗DFNN的含有复杂条款认股权证定价模型
孙 彬, 李铁克
(北京科技大学 经济管理学院 北京 100083)
基于滑动窗DFNN的含有复杂条款认股权证定价模型
孙 彬, 李铁克
(北京科技大学 经济管理学院 北京 100083)
将Black-Scholes模型与动态模糊神经网络相结合,构建一种含有复杂条款的认股权证定价模型.通过设定一定长度的滑动窗来保持采用固定长度的数据进行模型结果参数调整,同时采用动态调整前提参数策略,确保定价模型的泛化能力.以我国权证市场中认股权证阿胶EJC1为例进行分析,结果表明,提出的定价模型与RBF模型相比准确性较高,并且对权证价格走势判断较为准确.
认股权证定价; Black-Scholes模型; 滑动窗口; 动态模糊神经网络
0 引言
自Black-Scholes(B-S)期权定价模型建立以来,该模型便成为权证定价的理论基础[1],国内外很多学者对认股权证的定价都进行了深入的研究[2-4].但是权证价格的变化是模糊的,变化的规律是不清晰的,变化的结果具有高度容错性,并具有复杂的动态非线性特征.B-S定价模型难以反映这种复杂性,在实际操作上易产生价格偏误等问题.为了避免在严格假设下参数化模型的不足,神经网络模型在期权定价中得到了广泛的关注和研究[5-9].混合BP神经网络是由文献[6]提出并最早将其用于期权定价,它是通过BP网络来拟合参数化模型和实际市场价格差对期权进行定价.对混合BP神经网络的研究表明[7],由于其部分减轻了上述缺陷而使其预测结果要好于BP神经网络模型和经典的B-S模型.而模糊神经网络既可以解决传统模糊推理中隶属函数的系统设计,又可以解决神经网络的黑箱问题;并且通过将专家知识结合到模糊神经网络中,可以提高收敛速度、缩短训练时间.因此,模糊神经网络成为针对非线性系统仿真研究的一个热点,并形成了一个较为完善的体系[10-11].现有模糊神经网络主要存在4点不足:①网络结构选取主观化或在结构设计时仅利用样本的输入信息而未利用输出信息和误差信息,从而造成网络出现过训练或过拟合现象;②神经网络的作用都只是对模糊系统参数的学习和优化,并对可能的变化在参数上作自适应调整,而较少有针对网络结构的优化设计;③网络的学习方式多为BP算法,但是BP算法具有速度较慢且容易陷入局部极小点的缺陷;④网络多为静态模型,不适用于在线控制.
针对以上问题,作者结合B-S模型与动态模糊神经网络(dynamic fuzzy neural network,DFNN)建立含有复杂条款的认股权证定价模型;并通过设定滑动窗口使得模型保持采用固定长度的数据来调整参数,避免数据饱和.本模型可以实现参数估计与结构辨识同时进行以及对认股权证定价的动态在线控制.
1 含有复杂条款的认股权证定价模型
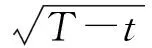

2 滑动窗动态模糊神经网络
DFNN是以认股权证定价公式(warrants pricing model,WPM)为基础,训练结构如图1(a)所示,用权证市场价格与WPM计算价格之差作为DFNN的指导信号.DFNN模型训练好之后,固定网络的权值、网络拓扑结构及模糊规则.根据新的权证输入数据,得到模型的定价输出,具体结构如图1(b)所示.
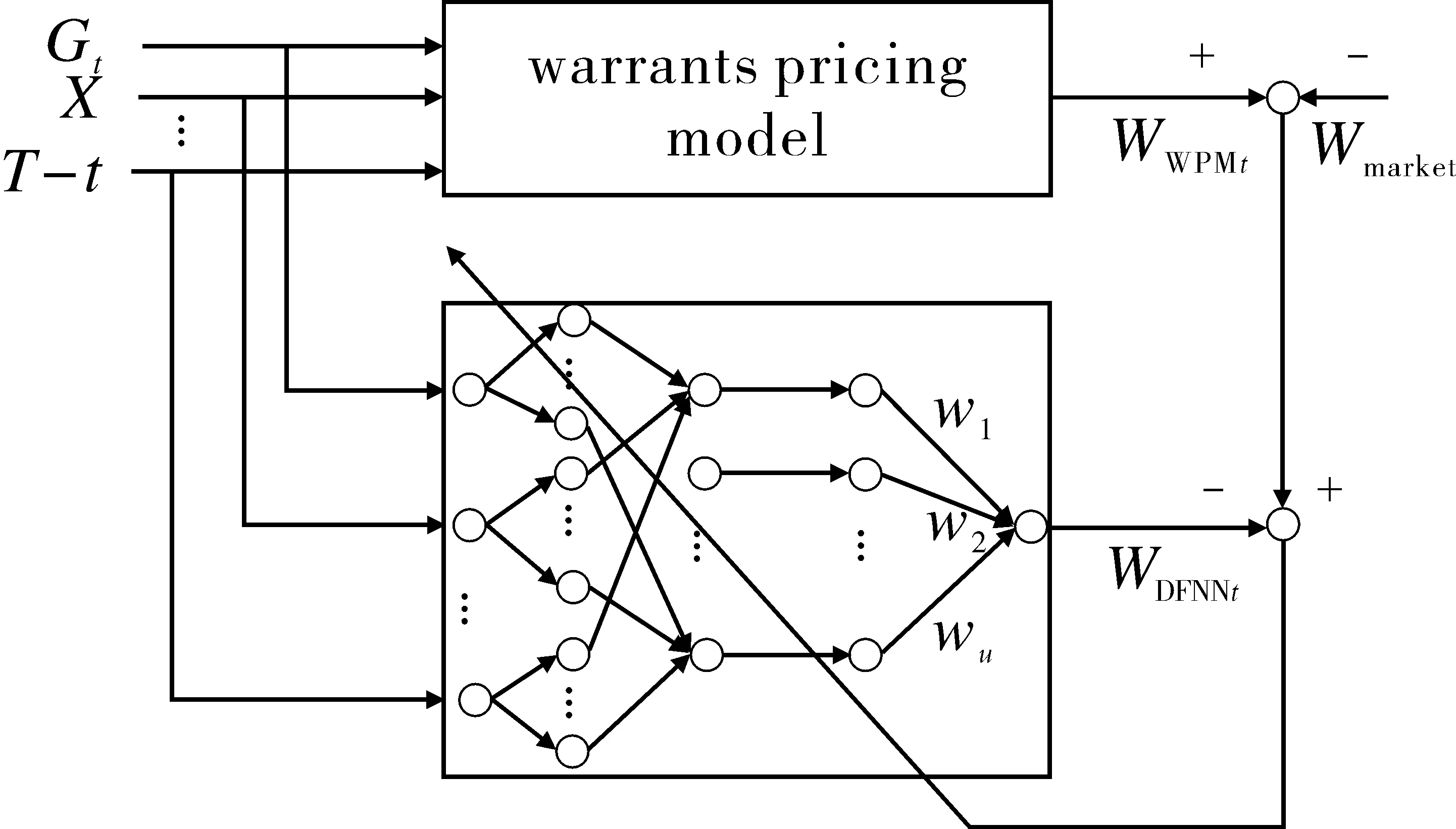
(a)
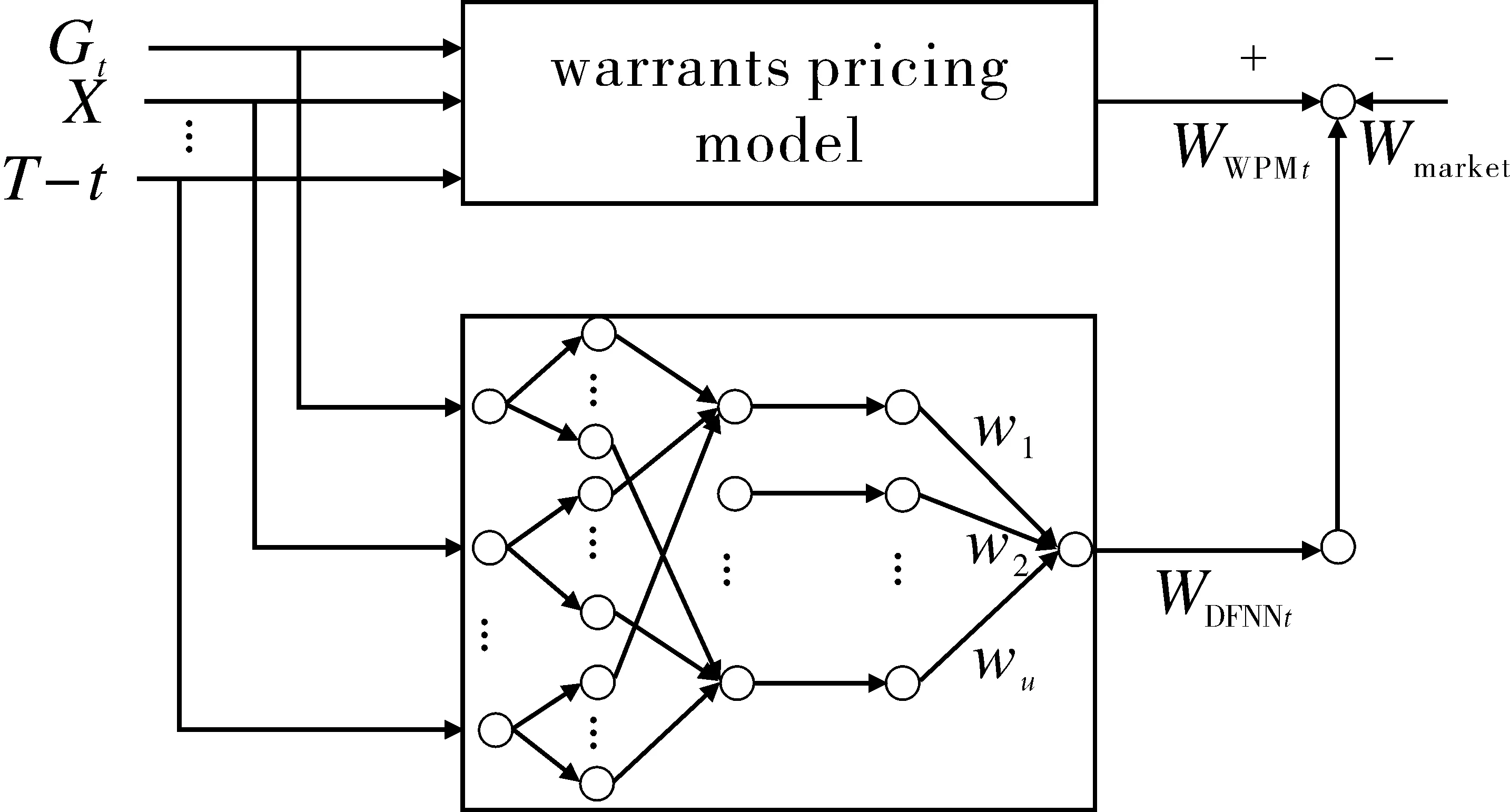
(b)
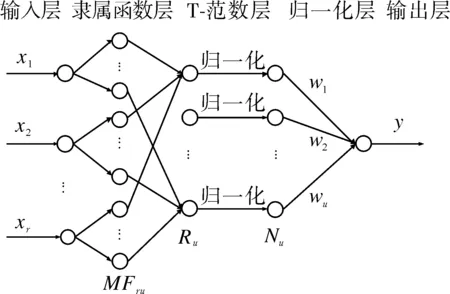
图2 DFNN的结构Fig.2 Structure of DFNN
2.1DFNN结构
DFNN的结构是一个扩展的径向基函数(RBF)神经网络与Takagi-Sugeno-Kang(TSK)模型相结合的模糊神经网络,结构如图2所示.
x1,x2,…,xr是输入的语言变量,y是系统的输出,MFij是第i个输入变量的第j个隶属函数,Rj是第j条模糊规则,Nj表示第j个归一化结点,wj是第j个规则的结果参数或者连接权,u是系统总的规则数,i=1,2,…,r,j=1,2,…,u.
第一层:输入层.每个节点代表一个输入的语言变量.
第二层:隶属函数层.每个节点分别代表一个隶属函数,该隶属函数采用高斯函数:
(1)
其中,μij是xi的第j个隶属函数,cij是xi的第j个隶属函数的中心,σj是xi的第j个高斯隶属函数宽度.r是输入变量数,u是隶属函数的数量,即系统总的规则数.
第三层:T-范数层.每个结点分别代表一个可能的模糊规则中IF-部分.第j个规则Rj的输出为
(2)
其中,X=(x1,x2,…,xr)∈Rr,Cj=(x1j,x2j,…,xrj)∈Rr,是第j个RBF单元的中心.
第四层:归一化层.这些节点为N节点,第j个节点Nj的输出为
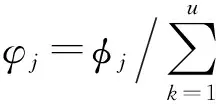
(3)
第五层:输出层.每个节点分别表示一个输出变量,该变量是所有输入信号的叠加,即
(4)
其中,y是输出变量,wk是THEN-部分或第k个规则的连接权.对于TSK模型,
wk=αk0+αk1x1+…+αkrxr,k=1,2,…,u.
(5)
将式(2)、(3)、(5)带入式(4),则
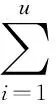
(6)
2.2DFNN学习算法
Step0初始化模型预定义参数:输入空间的最大长度dmax,最小长度dmin,衰减常数γ(0<γ<1);模型设定最大误差emax,期望精度emin,收敛常数β(0<β<1);初始高斯隶属函数宽度σ0;RBF神经元重叠因子k(k>1);RBF神经元宽度更新因子kw(kw>1);模糊规则显著性阈值kerr;
Step1当第一个观测数据(X1,t1)得到后,此时DFNN还没有建立起来,因此C1=X1,σ1=σ0;
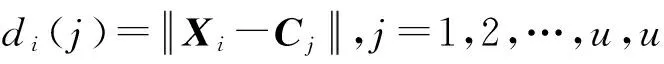
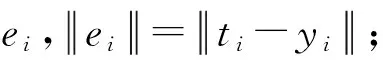
Step4当第i个观测数据(i=1,2,…,n;n>ls)进入滑动窗时,判断i≤ls是否成立,若是,则所有的数据保留在窗中,转Step 6;否则,转Step 5;
Step5窗中数据通过接受ls个最新的数据,并删除最旧的数据进行更新,转Step 6;
Step6根据文献[12]提出每个RBF单元的可容纳边界不是固定的而是动态调整的:开始可容纳边界设置较大,以实现全局学习,随着学习边界逐渐减小,开始局部学习.令动态参数kd=max[dmax×γi,dmin],判断dmin>kd是否成立,若是则转Step 7;否则,转Step 9;
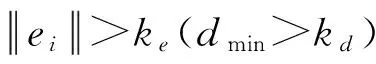
Step8根据文献[13]提出的误差下降率作为修剪策略:ηi反应第i个规则的重要性,ηi越大表示第i个规则越重要.判断ηi W=(α10…αu0α11…αu1…α1r…αur);Ψ=(φ,φX1,…,φXr)T∈R(r+1)u×n. Step11判断i 3.1实验数据及预处理 对含有复杂条款认股权证的定价研究将对认股权证的投资起直接的指导作用,同时也可以提供风险控制策略支持,因而具有重要的实际意义.以认股权证阿胶EJC1为研究对象,选取其上市时间2008-07-18至2009-04-09共175个样本数据进行定价分析,其中选取2008-07-18至2009-01-20的权证数据与标的股票数据作为模型的训练样本,2009-01-21至2009-03-24的相应数据作为测试数据.认股权证阿胶EJC1(031007)的标的股票为东阿阿胶(000423),发行人为山东东阿阿胶股份有限公司.权证存续起始日为2008-07-18,存续终止日为2009-07-18;行权起始日为2009-07-13,行权终止日为2009-07-17.公司的流通股股数N为40 244.28万股,认股权证份数m为13 094万份,执行比例n为1∶1,初始执行价X为5.50元;公司于2008-08-27日针对2007年业绩实施分红,8月28日除权后,认股权证的最新执行价X为5.434 9元. 因此,模型的输入指标为GT,X,T-t,r,σs,VG,i,Wi,VW,i,其中,Wi为认股权证第i天的日收盘价,VG,i,VW,i分别为标的股票与认股权证第i天与第i-1天成交量自然对数的差(i=1,2,…,164).考虑到DFNN要求对数据进行归一化处理,设样本数据为xi(i=1,2,…,n)转化为[-1,+1]区间的数据. 3.2实验评价指标 采用以下评价指标:v1是规格化的均方误差,v2是平均绝对差,v3是方向一致性指标.其中,v1与v2是对预测值偏离实际值的一种度量,值越小表示预测的结果越准确.v3则能衡量出定价方向的正确比率,值越大表示一致性越高.计算方法为 3.3实验环境与结果分析 采用Matlab语言在PC Pentium 4 /CPU 3.0 GHz /RAM 1.0 G上编程实现上述模型.为了测试模型的有效性,将模型对认股权证阿胶EJC1的定价与实际价格进行比较. 实验1:DFNN模型滑动窗参数对定价效果的影响. 窗长度ls在辨识时变系统中起着非常重要的作用.较小的ls将会导致极大地遗漏前面的数据,而较大的ls可能导致DFNN的更新能力下降,使得模型的参数无法辨识.如图3所示,当ls∈[90,100)时,v1随着ls值的变大而变小,v3先保持不变,后逐渐变大;当ls∈[100,118]时,v1随着ls的增大而逐渐平缓,同时v3先变大随后逐渐平缓;当ls∈(118,125]时,虽然v1仍有一定改善,但代表定价方向正确比率的v3却降低了.因此,经过比较,选取滑动窗长度ls=118. (a) ls与v1的关系图 (b) ls与v3的关系图 图4 非线性动态系统辨识Fig.4 Nonlinear dynamic system identification 实验2:DFNN模型与RBF模型定价评价指标比较. DFNN模型的各项评价指标分别为:v1=0.084 5<0.120 2,v2=0.017 0<0.021 4,v3=82.05>69.23,不仅在精确度方面比RBF模型有所提高,而且在定价方向一致性上有较大改善.DFNN模型以WPM模型的定价结果与权证实际结果的差值作为指导信号,并结合标的股票市场及权证市场中的交易量变化率等能够反应市场能量的指标,使得DFNN不仅具有传统权证定价一致性较好的优势,同时能通过DFNN智能学习真实市场中的信息,实现定价的精确性. DFNN模型能根据样本特征动态生成模糊规则,如图4所示,经过124个训练数据,规则数稳定在2.但规则数保持稳定不代表规则不变,当新的样本数据加入,前提参数(宽度)和结果参数一直保持更新,而且一条新规则的产生可能会剔除一条或两条已有的规则而同样保持系统的精确. 另外,模型可以根据自动生成的模糊规则建立针对含有复杂条款认股权证的专家规则库.设xi,j表示第j个输入样本的第i维向量(i=1,2,…,5,j=1,2,…,40),根据DFNN推导出模糊规则为 Rk:ifx1,jisμ1,kandx2,jisμ2,kandx3,jisμ3,kandx4,jisμ4,kandx5,jisμ5,kandx6,jisμ6,kandx7,jisμ7,kandx8,jisμ8,kthenuk,jisφk,j. 根据式(5)知,结果参数wk,j为 w1,j=517.75+180.94x1,j+12.60x2,j+434.04x3,j-276.95x4,j-283.50x5,j-16.39x6,j-217.96x7,j-5.12x8,j, w2,j=-514.59-184.81x1,j-13.01x2,j-429.89x3,j+273.83x4,j-281.63x5,j+16.02x6,j+221.02x7,j+5.19x8,j. 最后,由式(6)推出含有复杂条款的认股权证DFNN定价模型为y(X)=w1·φ1,j+w2·φ2,j. 针对含有复杂条款的认股权证构建了基于DFNN的定价模型.该模型无需对复杂、非线性且具有严重不确定性的金融系统提出经验性假设条件,可利用传统认股权证定价模型以及相关的输入/输出数据进行学习并进行预测.DFNN定价模型能够提取模糊规则,动态生成网络结点,自动进行输入空间划分.ERR修剪技术的应用,使得网络结构不会持续增长,避免了传统神经网络的过拟合及过训练现象,确保了定价模型的泛化能力.研究DFNN定价模型滑动窗长度的取值范围,并针对阿胶EJC1确定了最优窗口长度.仿真结果表明,所提出的DFNN认股权证模型定价准确性较高,具有传统认股权证定价模型对权证走势判断较为准确的特点,为研究认股权证定价提供了一种新思路,具有一定的理论意义和工程应用价值. [1] Merton R C.Theory of rational option pricing[J].The Bell Journal of Economics and Management Science,1973,4(1):141-184. [2] 孙彬.基于等价鞅方法下认股权证的定价模型[J].华北水利水电学院学报,2007(6):85-90. [3] Zhang Weiguo,Xiao Weilin,He Chunxiong.Equity warrants pricing model under fractional Brownian motion and an empirical study[J].Expert Systems with Applications,2009,36(2):3056-3065. [4] Yagi K,Sawaki K.The pricing and optimal strategies of callable warrants[J].European Journal of Operational Research,2010,206 (1):123-130. [5] Boek C,Lajbcygier P,Palaniswami M,et al.A hybrid neural network approach to the pricing of options[C]//IEEE International Conference on Neural Networks.Perth,1995:813-817. [6] Christopher A Z.Beyond Black-Scholes:a neural network-based approach to option pricing [J].International Journal of Theoretical and Applied Finance,2003,6(5):469-489. [7] Lajbcygier P.Improving option pricing with the product constrained hybrid neural network[J].IEEE Transactions on Neural Network,2004,15(2):465-476. [8] Panayiotis A C,Spiros M H,Chris C.Option pricing and trading with artificial neural networks and advanced parametric models with implied parameters[C]// IEEE International Joint Conference on Neural Networks.Budapest,2004:2741-2746. [9] Morelli M J,Montagna G,Nicrosini O,et al.Pricing financial derivatives with neural network [J].Physica A,2004,338(1/2):160-165. [10] Lin C T,Lee C S G.Neural Fuzzy Systems:a Neural-fuzzy Synergism to Intelligent Systems[M].New Jersey:Prentice Hall,1996:797. [11] Jang J S R,Sun C T,Mizutani E.Neuro-fuzzy and soft computing:a computational approach to learning and machine intelligence [J].IEEE Transactions on Automatic Control,1997,42(10):1482-1484. [12] Lee S,Kil R M.A gaussian potential function network with hierarchically self-organizing learning [J].Neural Networks,1991,4(2):207-224. [13] Lu Yingwei,Sundararajan N,Saratchandran P.A sequential learning scheme for function approximation by using minimal radial basis function neural networks[J].Neural Computation,1997,9(2):461-478. SlidingWindowedDFNNPricingModelofWarrantswithComplexTerms SUN Bin, LI Tie-ke (SchoolofEconomicsandManagement,UniversityofScienceandTechnologyBeijing,Beijing100083,China) A pricing model of warrants with complex terms was proposed based on dynamic fuzzy neural network (DFNN) and Black-Scholes model.In order to get optimized result-parameters of model with fixed-length time series data,a sliding window was set for DFNN.A dynamic adjustment approach of premise parameters was introduced to improve generalization ability of the model.Comparing with RBF pricing model,DFNN showed smaller deviation and higher accuracy in pricing EJiao EJC1. warrant pricing;Black-Scholes model;sliding window;DFNN F 830.91 A 1671-6841(2011)04-0104-06 2011-03-04 国家自然科学基金资助项目,编号70771008,70371057. 孙彬(1983-),男,博士研究生,主要从事金融工程及人工智能研究,E-mail:sunbinangel@yahoo.com.cn.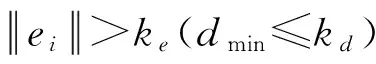
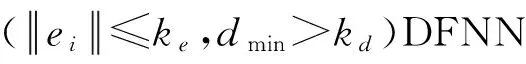
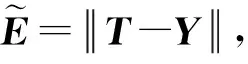
3 仿真实验与分析






4 结束语

