稳态的概率数据库探讨
江 彤
(湖南人文科技学院计算机科学技术系,娄底,417000)
稳态的概率数据库探讨
江 彤
(湖南人文科技学院计算机科学技术系,娄底,417000)
现实世界中存在着大量不确定性信息,传统关系数据库都视他们为空值。基于扩展传统关系数据库模型处理概率数据方面的不确定性,可建立一种处理概率关系数据库查询方法——稳态处理方法。该方法通过在关系模式中,为每条记录指定适当的概率,表示不确定性信息,同时依据事物之间的联系,确立事件的条件关系概率,其中最大条件关系概率值即为所查询事件的稳态。该方法对于处理大量不确定性信息,预测其最大可能性,具有重要意义。
不确定信息;条件关系概率;稳态
在数据库的基本研究中,数据分为确定性数据与不确定性数据。传统关系数据库的相关规则是建立在精确的数据之上,而不确定性数据充斥着整个世界,大致可分为模糊型和概率型两种,其中对模糊数据的研究在国内外已取得许多成果[1-3]。概率数据(probabilistic database)是指某一事件发生的可能性,文献[4-6]都是国外关于概率数据库研究的主要成果,大都表现在概率关系的定义上。2006年,Prithviraj Sen 和Amol Deshpande错误!未找到引用源。研究了概率数据库元组的描述和查询相互关联的元组,认为概率数据库的发展主要受到两个方面的限制:(1)当前的概率数据库对所举的事例过于简单,例如元组是相互完全独立的,这就使得在实际的应用中出现相互关联的数据时,不能够有效的计算。(2)大多数概率数据库只能解决用传统查询语句描述的限制了的查询语句。随着计算机网络的飞速发展和信息化的推进,概率数据库这种处理不确定性问题的数据库模型逐渐引起了人们的关注,但以前出现的概率数据库研究,认为元组在数据库中的存在具有不确定性、属性值具有不确定性、查询应答也具有不确定性。这使得人们在面对不确定问题时往往采取忽略的态度,在关系数据库中视他们为空值。然而解决不确定性问题、处理概率性数据的重大价值,使我们不得不重新定义概率数据模型。
本文为了处理概率数据方面的不确定性,建立了一种处理概率关系数据库查询的方法——稳态处理方法,通过在关系模式中,为每条记录指定适当的概率,表示不确定性信息,同时依据事物之间的联系,确立事件的条件关系概率,其中最大条件关系概率值最大即为所查询事件的稳态。
1 相关工作
由于世界是动态的,对象或事物存在与否本身具有一定的可能性,对于大量不确定的信息,在前人工作的基础上,我们继续用一个概率值表示事物发生的可能性。通常大家把事件发生与否看成随机事件,即事件存在n种可能时,每种可能发生的概率为1/n。随着人们遇到问题的复杂程度的增加,特别是对于同一事件,可以从不同的可能性角度算出不同的概率。另一方面,随着经验的积累,人们逐渐认识到,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示一定的稳定性。R.von米泽斯把这个固定数定义为该事件的概率,即概率的频率定义。
这里我们依照概率的频率定义,把A(张三,教授)的概率设为0.6,B(张三,教务主任)的概率设为0.4,具体设置如(表1,表2)所示,对于同一个对象依照离散的随机变量的分布情况,满足0≤ps≤1,且∑p(ps)=1的属性。张三的职务在教授和教务主任两种可能,同时教授和教务的工资也是个动态量。依照一般的查询处理,无法准确得出张三,李四的具体身份及工资情况。为了使概率数据模型适合关系数据模型的查询方法,我们以稳态来反映不确定事件在动态世界的常态,通过查询事件的稳态,从条件概率关系的分布式中取得事件的稳定状态。
概率关系模式上的一个元组由对象属性、动态属性、概率属性等组成, 它描述的不是传统关系数据模型中的简单对象, 而是动态对象( 包括动态的对象本身和对象的动态属性) 的一个事件连同该事件发生的概率。形式上它类似传统关系模式,实际是描述某事件发生的概率。所以不同的行描述的是不同的事件及其概率,同一事件不允许出现在同一关系之中。

表1 ZW表

表2 GZ表
2 方法概述
定义1 概率数据模式:我们扩展了文献[1]的有关概率的定义即事物随机试验的每一种可能为一个样本,它是最基本的元素。所有的样本构成事物的样本空间,且其样本空间满足p(Ω)=1 的特性。设r是数据库M的有一个实例,对于r事件发生的每一个可能,为一个样本点,r满足0≤p(r)≤,r事件发生的所有可能之和总为1的情况,由跟r类似的数据构成就是概率数据库。

张三是一个对象,其身份存在教授和教务主任两种可能,满足0.6+0.4=1的条件,其职务和工资的可能性也符合 0.3+0.3+0.28+0.12=1,李四跟张三的情形类似,都处于动态的关系中,由张三,李四构成的数据表就是一个关于表1动态变概率数据表。表中数据的概率属性是一个不确定性数据,是一个在有限的次数中积累的一个数据频率。
定义2 由概率的性质我们知道事件发生的概率之和满足等于1的条件。然而对于动态世界中的动态事件永远处于一种不确定的条件下,我们不可能对事件发生的各种可能做出有效的判断,这种不可能令数据库处于一种非稳定状态。
例如在已知的有限条件下,我们对动态对象M的概率化处理得到P(M(A))=0.6 (M(A)表示M发生事件A),P(M(B))=0.4 (M(B)表示M发生事件B),其满足P(M(A))+P(M(B))=1。这时,当出现M(C)时,显然无论P(M(C))多大,只要它发生,其和就大于1。
根据概率的频率定义,在事件无限次发生的条件下,P(i)将为一个固定值,即动态事务对象产生各种可能性的概率值的比值为一个稳定值。当事件存在的有限种可能性中,设其概率P(i)(i≥1),在满足(1)式的情况下,P(0);P(1):…:P(i)=M:N:…:Z,当i增加1或减少1时,满足仍然满足关系P(0);P(1):…:P(i)=M:N:…:Z不变。P(i+1)的值则通过如下求得:
(P(0)-P(i+1)*M/(M+N+…+Z)):(P(i+1)*N(M+N+…+Z))=M:N…:Z

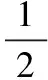
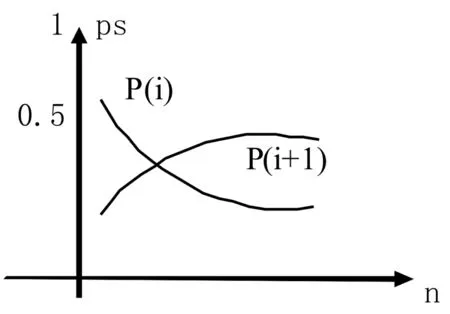
图1 概率变化
图1可以清楚的反映当原概率满足1的情况下,随着对象事件发生次数的增加出现新可能的变化,图中(ps表示概率,n表示事件发生的次数)。
如(表1)中,当在添加一个元组C(张三,系统分析师)时,其概率满足如下关系:A.ps :B.ps :C.ps=2/5 : 4/15 : 1/3 。这也反映了目前由于条件的限制,动态事件的各种可能性的记录结果处于一种不确定不稳定状态,其主要特点就是目前我们收集数据源的数据是不确定的,并且数据处理过程也会产生一些不确定的结果。
定义3 条件关系概率(Conditions probability):我们在已有的条件概率定义的基础上再定义,设A,B⊂M,m为M上的关系。如果x,y∈m,x≠y,∀c∈B,有x(A)=y(A)x(C)y(C),⟹A称为B前提事件,则元组x的可能值可看成在A事件发生的前提下B事件同时发生的可能性,即条件关系概率。令x是模式A的一个元组,x发生的概率用p(x)表示,y是模式B的一个元组, 概率是p(y),则p(x×y)=A▷◁B 。
如通过对表1、表2做笛卡尔积计算,得到条件关系概率值。通常情况下,关系数据库一个元组唯一表示一个对象(实体/联系)。而在概率数据模式中,每个元组不能唯一的表示一个对象,只能表示该对象的一种可能性分布。因而,依靠事件之间的关系虽然不能精确反映事物属性,却使事件的动态属性与传统的关系数据模式的静态属性转化,为预测和查询事件的最大可能奠定基础。
由于世界是动态的,对象或事件存在与否本身具有一定的可能性。在存在的前提下,事件的发生也具有一定可能性。因此,对于查询这些动态的数据的确定性记录很能够难实现,而只能依照事件发生的概率,来反映事件发生的稳定状态。
概率数据库中,元组本身描述的是动态的对象事件,每一个元组表示某一个对象事件,一个对象可能出现几个不同的事件,有几个元组描述。令所有的可能事件为一个集合,某一个事件发生的可能性,即为其发生概率。概率数据模式形象的反映了事件发生的概率情况。然而,这些动态生成的数据往往是对研究动态世界中的稳态产生干扰。如在(表三)中(李四,职务,工资,概率)关系里,其存在的四种可能使得我们无法对李四的身份得出精确的记录。
当遇到了不确定性问题,传统研究方式往往采取的“去除不确定性”方法避开对不确定数据的管理。这里我们必须承认数据中的不确定性问题,保留并处理不确定的中间结果,而不是通过种种确定化的手段去除不确定性,只有这样才能真正解决概率数据模式中的不确定问题。这里我们采取数据查询求取稳态的方法处理这种不确定性问题。
方法1 查询优化一:设概率关系模式{P1,P2,…,Pn}上i元组的概率值为Pi(0≤Pi≤1),对于该关系模式的查询结果按照Pi的大小排序,以MAX(Pi)--最大概率值反映事件的稳定状态。MAX(Pi)即为稳态。
对于概率关系模式{P1,P2,…,Pn}处理海量数据过程中,连接查询是我们解决处于动态世界中不确定问题的主要手段。然而对于海量数据不可避免地会出现按照Pi的大小排序时,出现MAX值相等的两个值。按方法1处理显然很容易让人产生迷惑。这时我们对数据进一步优化。

3 查询操作
实验是在一台有1G内存的AMD Athlon(tm) 64 X2 Dual Core Processor 3600+ 2.01GHz的微机上进行的,操作系统是Windows XP ,利用SQLSERVER2005实现各部分功能。
概率数据系统所要面对的数据已经不再局限于确定性的数据,而要处理很多非传统方式产生的数据,这些数据往往是不准确的,具有不确定性的本质。我们以(表1 ZW表,表2 GZ表)两表为例,对其我们无法实行精确查找。换句话说,我们查询出来的元组不精确。如在(表1)查询“张三“显示的将是(张三,教授,0.6),(张三,教务主任,0.4)两条记录。这里我们对表1查询的结果优化,即查询结果为(张三,教授,0.6)。
根据3.1根据定义1和定义2,对(表1,表2)查询。这里根据事件之间的条件概率关系,先对其做其做笛卡尔处理,然后进行查询。这里产生(张三,教授,4500,0.3),(张三,教授,5000,0.3)两条MAX记录,显然我们只能对其进行第二种优化处理方法。
SELECT ZW.姓名, ZW.职务,ZW.准确性 as 准确性1,ZG.准确性 as 准确性2,
ZG.工资,ZW.准确性 * ZG.准确性 as 条件概率
FROM GZ INNER JOIN
ZW ON ZW.职位 = GZ.职位
WHERE ZW.姓名 = '张三'
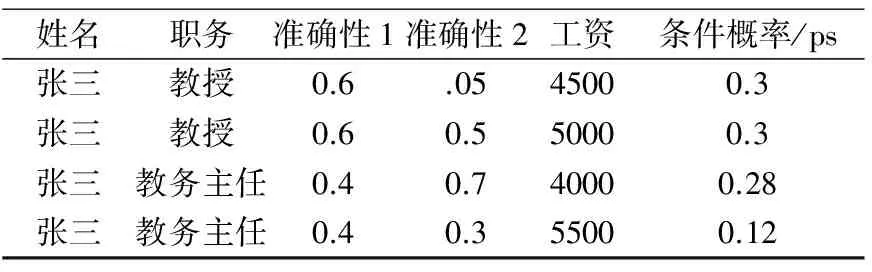
表3 条件概率关系的分布式反映(格式不对)
当某事件有n张子表,每张表中有n条记录,当我们对这n张表进行连接查询时,按照条件概率处理方法其时间复杂度为O(nn),很显然这种方法处理不恰当。由于我们需要的是在不确定性问题中反映事件稳定状态的数据,即最大的条件关系概率值。按照笛卡尔的运算方法,我们可以先对这n张表的每一张表的概率属性值排序。我们知道排序的时间复杂度为O(n2),这样我们处理查询的时间消耗明显减少。全文变量斜体问题
通过对每张表排序在一定程度上解决了查询的时间消耗问题,但同时产生了连接映射(join matching)不确定性问题,即模式匹配不确定性。
定义3 联接匹配(join matching): 以概率数据库中的所有元组为全集M,每张Table的元组的作为集合T,T∈M,有交集Ri=Ti∩Tm(Ti,Tm∈M),当对数据查询是先求两表间的交集Ri,再依据其进行匹配查询。
如在(表1,表2)中,其交集为职务。故对‘张三’进行查询时,表1的MAX值为0.6,对应教授职务,表2的MAX值为0.5,对应教授职务,匹配成功。
依据前面的研究工作,我们对(表1)各元组发生的可能概率化,使不确定的动态信息数字化,以便使用关系数据的查询模式。通过以上处理后得到表1、表2概率关系。
我们依照定义对检索规则做如下规定:
先检索该人的职位,取职位对应的概率的最大值,再依据检索出的职位检索其对应的工资及概率的最大值,再检查是否联接匹配,最后依照条件概率的乘法定理,得到其条件概率。
所得结果的概率值最大,反映了其在动态世界中出现的可能性最大,把它作为其稳态。
SELECT top 1 ZW.姓名, ZW.职务,
ZW.准确性 as 准确性1,ZG.准确性 as 准确2,ZG.工资,
ZW.准确性 * ZG.准确性 as 稳态
FROM ZW INNER JOIN
GZ ON ZW.职务 = CZ.ZW
WHERE ZW.姓名 = '李四'
order by ZW.准确性 * GZ.准确性 desc

表4 效果
若存在条件概率相等的情况则输出工资期望(职位对应的概率与职位对应的的薪资的概率及薪资的乘积) 相对较高的记录所对应的职务及工资。
SELECT top 1 ZW.姓名, ZW.职务,
ZW.准确性 as 准确性1,ZG.准确性 as 准确2,ZG.工资,
ZW.准确性 * ZG.准确性 as 稳态
FROM ZW INNER JOIN
GZ ON ZW.职务 = CZ.ZW
WHERE ZW.姓名 = '张三'
order by ZW.准确性 * GZ.准确性 * GZ.工资desc

表5 效果
本文建立了一种处理概率关系数据库查询的方法——稳态处理方法,主要通过分析了动态世界中大量不确定事件的内在联系,对事件发生的可能性进行了概率化,将产生事件之间的条件关系概率,作为事件发生的参考依据,同时把事件发生的最大条件关系概率作为事件的准确性,其中最大条件关系概率值最大即为所查询事件的稳态,以反映事件的动态属性。
[1]汪荣贵,张佑生,彭青松.条件概率关系数据库模型[J].微电子学与计算机,2002,21(9):7-11.
[2]李石群,郑鹏,周洞汝.一种灵活的概率关系数据库模式及代数[J].计算机工程与应用,1999, 35 (11):23-24.
[3]姬东耀,张军英.一个概率关系专家数据库模型[J].计算机工程与应用,1999,35(6):75-77.
[4]蒋运承,张师超.一个不确定性数据库模型及其语义[J].计算机科学.1999,6(21):78-81.
[5]王洁,鞠实儿.数据库中不完善信息的逻辑描述[J].华南理工大学学报,2003,3(5):93-96.
[6]FAGIN R, LOTEM A, NAOR M. Optimal aggregation algorithms for middleware[J]. In Proceedings of the twentieth ACM IGMODSIGACT-SIGART symposium on Principles of atabase systems, 2001:102-113.
(责任编校:光明)
DiscussiononSteady-stateDatabases
JIANGTong
(Department of Computer Science and Technology, Hunan Institute of Humanities, Science and Technology, Loudi 417000, China)
There is a lot of uncertain information in the real world, and traditional relation database only regards it as null. Based on expanding the uncertainty of the traditional relation database model dealing with probability database, we may establish a method which called steady-state approach to deal with the probability of relational database queries. We designate the suitable probability for each record to express uncertainty information. At the same time, based on the links between things, we establish the conditions for the relationship between the probability of events, and the greatest probability is the largest event of inquiries by state. The method for dealing with a large number of uncertainties and forecast the possibility of its largest is very important.
uncertain information; condition relationship probability; steady-state
2011-07-12.
湖南省教育厅科学研究项目(11C0699)。
江彤(1978— ),女,湖南双峰人,湖南人文科技学院计算机科学技术系讲师,硕士,研究方向:数据处理。
TP311.123
A
1673-0712(2011)05-0116-04

