运用广义对称妙解竞赛题——2011年全国初中数学竞赛压轴题的解法探究

●(成功中学 安徽马鞍山 243000)

运用广义对称妙解竞赛题
——2011年全国初中数学竞赛压轴题的解法探究

●汪宗兴(成功中学 安徽马鞍山 243000)

数学家波利亚在其著作《怎样解题》中给出一个宏观的解题程序，分成4步：弄清题目、拟定计划、实现计划、回顾(即解题后的反思)．波利亚重视解题后的思考，把其作为数学解题的一个重要步骤，他认为一个问题解决后，解题者应该考虑有没有其他的解题方案，有没有更一般的或特殊的结论．笔者欲尝试运用波利亚的解题表，现结合2011年全国初中数学竞赛的压轴题，谈谈笔者的收获.

(2011年全国初中数学竞赛试题)

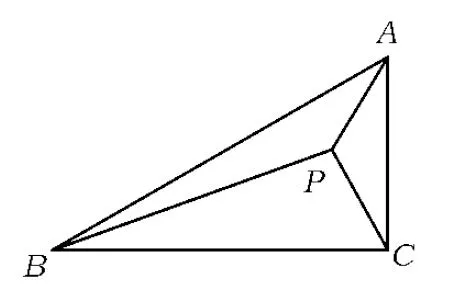
图1

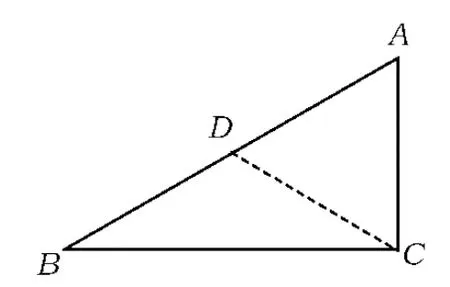
图2

为表述方便，现将以下结论作为引理：

引理在△ABC中，∠BAC=60°，AB=2AC，则△ABC是直角三角形且∠ACB=90°．

证法1如图2，取AB的中点D，连结CD.由AB=2AC，得

AC=AD=BD.

又∠BAC=60°，知△ACD是等边三角形，从而

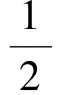
因此△ABC是直角三角形，此时

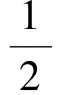
证法2如图3，延长AC至点D，使DC=AC，连结BD．由

AD=2AC=AB，

及∠BAC=60°，可知△ABD是等边三角形，由等腰三角形的“三线合一”性质可得BC⊥AC，此时

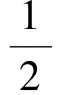
图3

思路探索由引理和△ABC边、角的数量关系可知，任求出一条边的长度即可求出该三角形的面积．已知长度的3条线段PA,PB,PC有公共的端点P，如何发挥这个条件的作用呢？考虑到这是一个特殊的直角三角形，给出长度的3条线段有公共端点这一特点，联想类似的问题：利用旋转求角度，如已知正方形内一点到3个顶点的距离，求角度；已知等边三角形内一点到3个顶点的距离，求角度．根据解题经验，首先考虑利用旋转变换解决此题.初步思考，因图中找不到相等的线段，故不具备旋转的条件．初次失败后，由于之前曾利用网格巧妙解决等腰直角三角形内一点到3条边的距离问题，试探此题能否建立适当的网格，也未获成功.看来孤立运用某个条件，很难找到解题思路，综合考虑或许才有出路.如何利用题中30°，60°等条件？旋转不成，再试用轴对称变换，发现点P关于CA，CB的对称点D，E和顶点C在一条直线上……，画出图形，很快发现各种条件都能巧妙应用，尝试终获成功(见解法1)．

解法1思路:利用轴对称变换．

如图4，作点P关于边BC，AC，AB的对称点D，E，F，连结DB，DC，EA，EC，FA，FB，FD，FE.由轴对称性质，得

从而

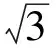
于是

DE2+FE2=42+32=52=DF2,

得

∠DEF=90°，

因此

2S△ABC=S△BDF+S△DEF+S△AEF=

即

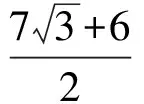
(注：求△AEF的面积可利用初中知识解决.)

笔者反思(1)前面方法未成功的原因是什么;(2)有没有其他更好的方法呢,轴对称变换能解决此题，旋转变换真的无“用武之地”吗?

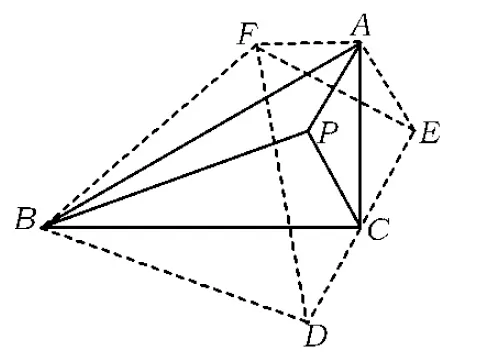
图4

图5

(注：此表示方法的含义是将△APC以A为旋转中心，顺时针旋转60°后，再进行同向位似变换，且△APC与△ADE的位似比是1∶1．角度前有负号的表示按逆时针方向旋转，下同.)

由引理知△ABC是直角三角形，从而

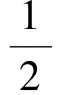
(注：此步骤各种解法中都要用到，这里统一给出，后面解法中限于篇幅，不再重述.)

如图5，将△APC绕点A顺时针旋转60°至△ADE，连结PD，则

从而△PAD是等边三角形.又由AB=2AC,得

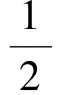
取PA的中点F，连结FD，FE，则

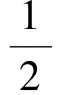
由等边三角形的性质，可得

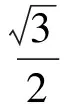
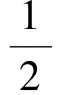
于是

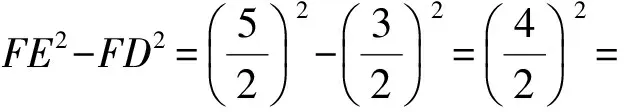
22=DE2,

从而△EDF是直角三角形，且∠EDF=90°，可得

∠APC=∠ADE=∠ADF+∠EDF=

30°+90°=120°.

作CG⊥AP于点G，则

∠CPG=180°-∠APC=60°，

于是

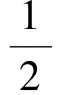
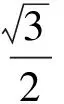
从而

因此

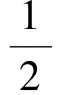
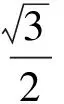
(注：在求出∠APC=120°之后，求AC2可以利用余弦定理求出，但考虑到初中学生的实际水平，这里给出利用勾股定理求AC2的过程，后面解法限于篇幅，只给出求∠APC的过程.)

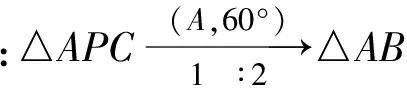
如图6，在△ABC外作△ABD，使得

∠DAB=∠PAC，∠ABD=∠ACP，

则△ABD∽△ACP，连结DP，得

AB=2AC，

于是△ABD和△ACP的相似比为2∶1，即

因此

∠DAP=∠DAB+∠BAP=

∠PAC+∠BAP=∠BAC=60°.

由AD∶AP=2∶1，及引理知∠APD=90°，从而

于是

BD2+PD2=42+32=25=BP2，

即

∠BDP=90°，

于是

∠APC=∠ADB=∠ADP+∠BDP=

30°+90°=120°.

后面过程同上,略．

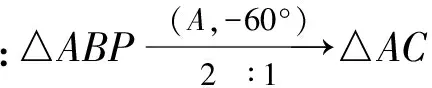
(过程略.)

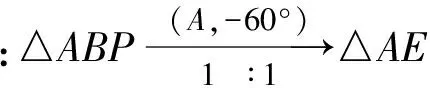
(过程略.)

图6

图7

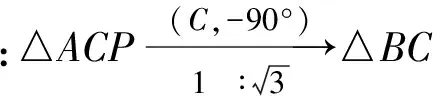
如图7，在△ABC外作△BCD，使得

∠BCD=∠ACP，∠CBD=∠CAP，

又

∠PCD=∠PCB+∠BCD=

∠PCB+∠ACP=∠ACB=90°，

连结PD，得∠PDC=30°，PD=2PC=4，从而

BD2+PD2=32+42=25=PB2，

得

∠BDP=90°，

于是

∠APC=∠BDC=∠BDP+∠PDC=

90°+30°=120°.

后面过程同上．

(过程略.)

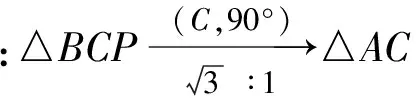
(过程略.)

(过程略.)

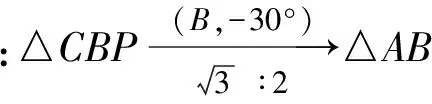
(过程略.)

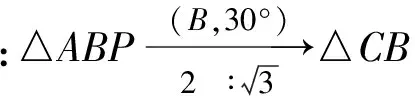
如图8，在△ABC外作△BCD，使得

∠BCD=∠BAP，∠CBD=∠ABP，

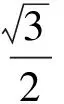
从而

∠PBD=∠PBC+∠CBD=

∠PBC+∠ABP=∠ABC=30°，

作DE⊥PB于点E，则

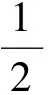
从而

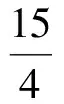
于是

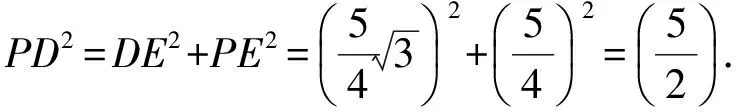
又

得

PD2=PC2+DC2,

从而

∠DCP=90°，

于是

∠APC=∠BAP+∠BCP+∠ABC=

∠BCD+∠BCP+∠ABC=

∠DCP+∠ABC=90°+30°=

120°．

后面做法同上，略．

图8

图9

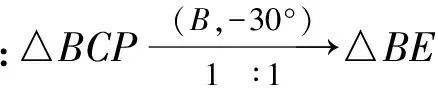
如图9，将△BCP绕点B逆时针旋转30°至△BED，则

DE=PC=2，BD=BP=5，BE=BC，∠DBE=∠PBC，∠BED=∠BCP，

从而

∠PBD=∠PBA+∠DBE=

∠PBA+∠PBC=∠ABC=30°.

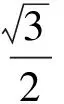
即

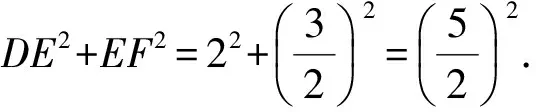
DE2+EF2=DF2,

即

∠DEF=90°，

于是

∠APC=∠BAP+∠BCP+∠ABC=

∠BEF+∠BED+∠ABC=

∠DEF+∠ABC=

90°+30°=120°．

后面做法同上，略．

(过程略.)

图10

解法14思路:采用代数方法，建立平面直角坐标系，运用解析法

由引理知△ABC是直角三角形(过程略)．如图10，以C为原点，CB所在的直线为x轴，CA所在的直线为y轴，建立平面直角坐标系．设AC=a，则

于是

由两点之间的距离公式，得

PC2=(x-0)2+(y-0)2=x2+y2=22=4;

于是

又

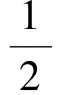
由引理，只要求出a2的值即可．由式(2)，得

x2+y2-2ay+a2=3,

即

4-2ay+a2=3,

化简得

2ay=1+a2.

(4)

由式(3)，得

即

得

(5)

(6)

于是

即

令a2=y，得

48y=(3t-21)2+3(1+y)2,

即

y2-14y+37=0,

解得

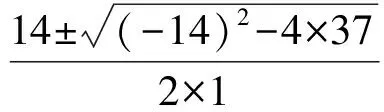
由式(5)得

解得

a2>7，

即

y>7．

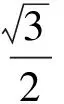
笔者反思从上述解法可以看出：解法1运用了轴对称变换；解法2～13都运用了旋转变换，解法2～5以点A为旋转中心，顺(逆)时针旋转60°，解法6～9以点C为旋转中心，顺(逆)时针旋转90°，解法10～13以点B为旋转中心，顺(逆)时针旋转30°，解法3,4,6,8,10,11还运用了位似变换;解法14利用代数方法，建立平面直角坐标系，反复运用两点之间的距离公式，计算出△ABC的面积．其中渗透数形结合的思想，容易理解，但计算繁琐．

从解法2到解法13，对称思想体现得淋漓尽致．从地位上看，△PAB,△PBC,△PAC平等，点A,B,C平等，都可以作为旋转中心，3个内角平等，30°,60°,90°都可以作为旋转角，顺时针旋转与逆时针旋转平等.正是受对称思想的启发，才想出上述众多形似本质相同的解法．正如波利亚曾说：“当你找到第一棵蘑菇后，要环顾四周，因为它们总是成堆生长的．”笔者在解决此题的过程中，收获甚大！

数学解题的目标应使得学习者获得对数学本质规律更为真实的理解，并在数学领域获得可持续的发展．波利亚认为解题过程主要是问题的变换过程，“我们必须一再变换它，重新叙述它，变换它，直到最后成功地找到某些有用的东西为止”.由上述问题的各种解法可见，如果平常讲解习题时注重解题后思考，注重数学思想的渗透，今后教学将可演绎更多无限精彩的课堂，教给学生有用的东西！

[1] 孙维刚．孙维刚谈立志成才[M].北京：北京大学出版社，2009．