《数学通报》1898号问题的简解及应用
● (浙江师范大学初阳学院 浙江金华 321004)
《数学通报》1898号问题的简解及应用
●徐杭(浙江师范大学初阳学院 浙江金华 321004)
《数学通报》2011年第3期刊登了郭富喜老师提供的1 898号问题的解答,过程有点繁琐,方法不易想到.现笔者提供如下的一种简解.
原题求值:(tan85°-tan5°)(tan80°-tan10°)(tan75°-tan15°)(tan70°-tan20°)(tan65°-tan25°)(tan60°-tan30°)(tan55°-tan35°)(tan50°-tan40°).
简解先对第1项进行化简,得
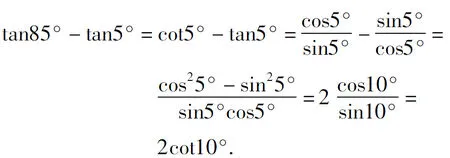
同理,其他项化简后,依次为2cot20°,2cot30°,2cot40°,2cot50°,2cot60°,2cot70°,2cot80°.结合公式cotα·cot(90°-α)=1得
原式=28(cot10°cot80°cot20°cot70°cot30°cot60°cot40°cot50°)=28=256.
本题的简解,其实就是应用了三角函数解题中的“切割化弦”方法,即将题中出现的正切、余切函数,正割、余割函数化为弦函数(正弦、余弦函数).常用的公式有:

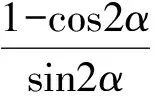
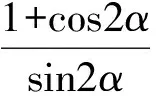
活用切割化弦方法,对三角函数的解题有很大帮助.下面举例说明之.
例1求cot80°+csc40°的值.
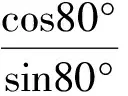

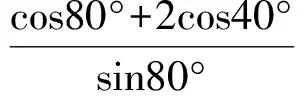
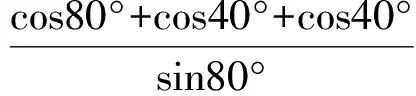
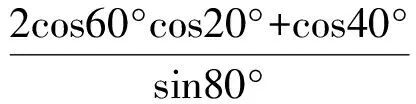

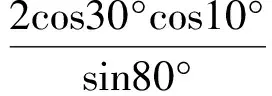
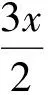
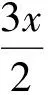

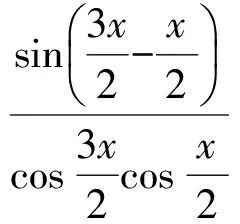
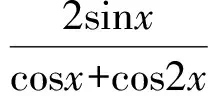


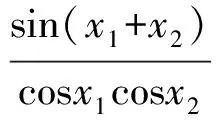

由
得
2sin(x1+x2)>0,cos(x1+x2)>0,0 从而 0 由此得 结合 得 即 以上3个例题都充分利用了切割化弦以及和差化积与积化和差公式.但是在求三角函数问题时,也不一定是一遇到“切”和“割”就立刻全部化成“弦”进行求解.而是要注意审题,切割化弦应把握一定的度.下面一个例子可供参考. 例4求值:cot15°cot25°cot35°cot85. 解原式=tan75°tan65°tan55°tan5° = tan75°tan15°=1.