一维分子晶体模型中立方型相互作用引起的孤子激发

李 圳，陈 浩

(华南师范大学物理与电信工程学院， 广东广州 510631)

在极性晶体中运动的电子，其库仑势使周围正负离子移位而产生极化，形成一个围绕电子的极化场．极化场又反过来作用于电子，使其能量和状态等发生改变，并伴随着电子在晶格中运动．这样一个相互作用的整体就是极化子．极化子效应降低电子的能量,并使电子有效质量增加．几十年来极化子问题一直在固体物理中扮演着相当重要的角色[1-7]．近年来，由于低维系统非线性元激发的研究进展，重新引起人们对于一维极化子理论的兴趣．而一维分子晶体模型中孤子激发态的存在也一直引起人们的重视，并已做过广泛的研究[8-11]．本文研究立方型相互作用下的一维分子晶体模型中的孤子激发解，求出了孤子的峰宽和峰值．虽然这一方程的解具有与原文献不同的形式，但在忽略立方型相互作用后，仍与通常极化子解[1]一致．

1 运动方程和解

考虑立方型相互作用后的一维分子晶体模型的Hamiltonian量为[1]：

H=He+Hint+Hp,

其中

(1)

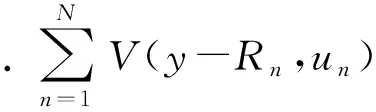
根据Holstein，我们可假定波函数：

(2)

满足Schrodinger方程．这里an依赖于时间t和晶格振动位移un，表示电子在第n格点上的概率幅；φn(y,un)为第n格点上的局域化的分子轨道，满足方程：

E(un)φn(y-Rn,un),

(3)

式中本征值E(un)只与分子振动的位移量un有关．取线性近似，得到：

E(un)=-Aun.

(4)

由式(1)～(4)及Schrodinger方程，得到an的运动方程：

(5)

式中

Jm,n=

是双中心交叠积分．-Aun项代表电子与晶格间的相互作用势．忽略Jn,n=1对un的依赖．设Jn,n±1=-J,则：

(6)

取绝热近似，即略去式(6)中的晶格振动的动能项，则得：

J(an+1+an-1)=Ean,

(7)

(8)

由能量极小条件∂E/∂um=0可推出：

在ω2a≪σ2时，上式的解为：

(9)

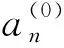
(10)

将式(9)、(10)代入式(7)可化解为：

(11)

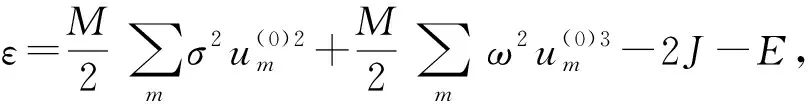
(12)

(13)

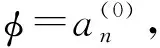
φ″+2γφ3-3βφ5-αφ=0．

则：

φ′2=φ(βφ4-γφ2+α),

(14)

即：

(15)

其中a2+b2=γ/β,a2b2=α/β．

方程(15)可化解为：

(16)

求解可得：

即：

(17)

(18)

解方程(18)得：

(19)

则：

代入方程(17)得

(20)

为一维分子晶体模型中考虑立方型相互作用后的孤子激发解，其中，

(21)

(22)

其中，Lp为考虑立方型相互作用后孤子的峰宽，Lp0为通常极化子的峰宽[1]．

(23)

(24)

其中，ps为考虑立方型相互作用后孤子的峰值，ps0为通常极化子的峰值[1]．

当ω=0时，即没有立方型相互作用存在时，β=0．此时，

(25)

与通常极化子的解[1]一致．此时的峰宽、峰值为式(22)、(24)所示．即在忽略了立方型相互作用的近似下，孤子激发的运动解回复于通常的极化子解．

2 结果和讨论

考虑立方型相互作用后，孤子激发的峰宽、峰值及孤子解随立方型相互作用的变化关系，如图1～图3所示．

图1 孤子的宽度随立方型相互作用的变化Figure 1 The change of the width of the soliton with the cubic interaction term

图2 孤子的峰宽随立方型相互作用的变化Figure 2 The change of the peak of the soliton with the cubic interaction term

图3 ω2取不同值时孤子解的比较Figure 3 The compare of solutions when ω2 take different valves

3 小结

一维分子晶体模型中如果考虑色散项的影响[10]，其孤子激发的特征值会受到影响，导致孤子的峰宽变宽，峰值变小，从而破坏了孤子的稳定性．而本文研究了立方型相互作用下一维分子晶体模型中的孤子激发问题，从立方型相互作用下一维分子晶体模型的哈密顿量出发，在绝热近似的条件下，得到运动方程，求出了孤子激发的运动解以及孤子的峰宽、峰值．在此主要关注立方型相互作用系数ω2的存在和变化对孤子特征值的影响．由上面的分析可以得到ω2项的存在同样也会使得孤子的峰宽变宽，峰值变小．由此可知：立方型相互作用项同色散项一样，都是孤子的弥散项，它们影响了孤子激发的特征，如峰值、峰宽，从而均不利于孤子激发的稳定性．

参考文献：

[1] HOLSTEIN T.Studies of polaron motion：PartⅠ.The molecular crystal model[J].Ann Phys,1959,8:325-342.

[2] SCHUTTLER H b,HOLSTEIN T.Dynamics and transport of a large acoustic polaron in one dimensional[J].Ann phys,1986,166:93-163.

[3] HOLSTEIN T.Dynamics of self-localized charge-carries in quasi 1-D solids[J].Mol Cryst Liq Cryst,1981,77:235-253.

[4] ZHANG C L,JECKELMANN E,WHITE S R.Dynamical properties of one-dimensional Holstein model[J].Phys Rev B,1999,60(20):14092-14104.

[5] HOLSTEIN T,TURKEVICH L A.Field theory for the one-dimensional optical polaron[J].Phys Rev,1988,B38:1901-1937.

[6] TEKIC J,IVIC Z,ZEKOVIC S,et al.Kinetic properties of multiquanta Davydov-like solitons in molecular chains[J].Phys Rev E,1999,60(1):821-825.

[7] CASTRO Neto A H,CALDEIRA A O.Alternative approach to the dynamics of polarons in one dimension[J].Phys Rev,1992,B46:8858-8875.

[8] 任学藻,廖旭,刘涛,等.一维分子晶体中的极化子[J].原子与分子物理学报,2006,23(4): 616.

REN Xuezao,LIAO Xu,LIU Tao,et al.Polaron of one-dimensional molecular crystals[J]. Journal of Atomic and Molecular Physics,2006, 23(4): 616.

[9] 许长谭,庞小峰.一维反铁磁分子晶体NENP中的孤立子激发[J].原子与分子物理学报,1996,13:508.

XU Changtan,PANG Xiaofeng.Solitary excitation in 1D antiferromagnetic molecular crystal NENP[J].Chinese Journal of Atomic and Molecular Physics, 1996,13:508.

[10] CHEN Hao,CHEN Yuan.On optical polarons in one dimensional molecular-crystal chains[J].Chinese Phys Lett,1996,13:617-620.

[11] 李正中.固体理论[M].北京：高等教育出版社，2002:363-367.