分数阶反应-子扩散方程的高阶隐式差分格式及其稳定性分析
梁 娜 叶 超
(1.咸宁学院数学与统计学院,中国 咸宁 437100;2.湘潭大学数学与计算科学学院,中国 湘潭 411105)
分数阶微分方程被广泛地应用到自然科学与工程学领域,引起了科研人员的重视.Metzler和Klafter在其综述性文章[1]中指出分数阶微分方程已经成为描述反常传播过程的一种基本工具.Machado等介绍了分数阶微积分理论在近30年的发展概况[2],分数阶导数,分数阶微分方程的解法与应用的一些基本理论[3]可见于Podlubny的经典著作.近年来,有关分数阶微分方程的解析解问题[4-7]取得了很多成果,然而这些解时常包含一类特殊而又复杂的函数,如Mittag-Leffler函数,这给实际的应用带来不便.因此有必要去研究分数阶微分方程的数值解法.
迄今为止,分数阶扩散方程的高阶数值方法很少.CHEN等讨论了一种非线性反常扩散方程的数值解法[8],提出了一种时间一阶,空间二阶的隐式差分格式,并利用Fourier方法对格式做了理论分析.Zhuang等利用积分的手段对一反常子扩散方程[9]进行离散,得到了一种时间一阶,空间二阶的隐式差分格式,采用能量方法给出了格式的稳定性与收敛性分析,并通过改进,提高了时间误差阶.Cui对一种分数阶扩散方程首次采用了一种紧致有限差分方法[10],得到了一种新的空间四阶,时间一阶的隐式差分格式.Chen等考虑了一种变阶的反常子扩散方程[11],基于Riemann-Liouville导数的Gr¨uwald-Letnikov离散以及结合四阶的紧致差分算子对空间二阶导数近似,得到了高阶隐式差分格式.作者利用一种新的积分手段,对反应-子扩散方程[12]进行离散,并使用紧致有限差分方法,提出了一种新的高阶隐式差分格式.
1 隐式差分格式
考虑一种反应-子扩散方程:
(1)
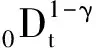
设方程(1)满足初始条件以及Dirichlet边界条件:
u(x, 0)=φ(x), 0≤x≤L;u(0,t)=φ1(t);u(L,t)=φ2(t), 0 (2) (3) 令 则(3)式可以表示为u(xj,tk+1)=u(xj,tk) +I1+I2+I3. 对于I1,我们采用如下近似, 引理1的证明参见文献[5].引入序列{bj},bj=(j+1)γ-jγ,j=0,1,…,N. 引理2{bj}(j=0,1,…,N) 满足b0=1,0 引理2的结论显然成立.由引理1,有 对于R11,根据Lagrange中值定理, 可得 由以上分析可以得到I1的整体近似为 对于I2,仍用类似于I1的近似方法,可得I2的整体近似为 至于I3, 我们采用梯形求积公式可得:I3=τ(f(xj,tk+1)+f(xj,tk))/2+O(τ3). 由以上可以得到如下引理. 引理3如果u(x,t) 满足引理2,则有 (4) j=1,2,…,M-1;k=0,1,…,N-1, (5) 定理1隐式差分格式(5)存在唯一解. 证事实上,(5)可以写成矩阵的形式: 其中 (6) εk(x)可以展成Fourier级数的复数形式 (7) εk(x) 满足 (8) (9) (10) 定理2如果vk(m) 满足(10)式, 则必有|vk(m)|≤|v0(m)|. 证在(10)式中令k=0 ,则有 利用引理2,知0 定理3隐式差分格式(5)无条件稳定. 证由定理2以及(14)式, 有 考虑下列一个带初边值条件的分数阶反应-子扩散方程 (11) (11)的精确解为u(x,t)=extγ+2.定义上述问题的精确解与数值解的最大误差为 取不同的空间步长,时间步长以及γ,并利用隐格式(5),计算(11)的精确解与数值解的最大误差.从表1的结果可知:该格式的稳定性好,在同步长下,精确解与数值解的最大误差随γ的增大而增大.表2与表3的结果同文中所给的误差阶较吻合. 表1 精确解与数值解的最大误差(E∞) 表2 精确解与数值解的最大误差(E∞),γ=0.2 表3 精确解与数值解的最大误差(E∞),γ=0.2 参考文献: [1] METZLER R, KLAFTER J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach[J].Phys Rep, 2000, 339(1):1-77. [2] MACHADO J T, KIRYAKOVA V, MAINARDI F. Recent history of fractional calculus[J]. Commun Nonlinear Sci Numer Simulat, 2011, 16(3):1140-1153. [3] PODLUBNY I. Fractional differential equations[M]. San Diego:Academic Press, 1999. [4] LIU J Y, XU M Y. Some exact solutions to Stefan problems with fracional differential equations[J]. J Math Anal Appl, 2009,351(2):536-542. [5] LIANG J R, REN F Y, QIU W Y,etal. Exact solutions for nonlinear fractional anomalous diffusion equations[J].Physica A, 2007, 385(1):80-94. [6] 张颖超.用径向基函数解偏微分方程[J].湖南师范大学自然科学学报,2011,34(5):1-6. [7] 颜宝平.一类倒向随机微分方程的比较定理[J].湖南师范大学自然科学学报,2011,34(4):26-28. [8] CHEN C M, LIU F, TURNER I,etal. A Fourier method for the fractional diffusion equation describing sub-diffusion[J]. J Comput Phys, 2007, 227(2):886-897. [9] ZHUANG P, LIU F, AHN V,etal. New solution and analytical techniques of the implicit numerical method for the anomalous subdiffusion equation[J]. Siam J Numer Anal, 2008, 46(2):1079-1095. [10] CUI M R. Compact finite difference method for the fractional diffusion equation[J]. J Comput Phys, 2009,228(20):7792-7804. [11] CHEN C M, LIU F, AHN V,etal. Numerical schemes with high spatial accuracy for a variable-order anomalous subdiffusion equation[J]. SIAM J Sci Comput, 2010,32(4):1740-1760. [12] CHEN C M, LIU F, BURRAGE K. Finite difference methods and a Fourier analysis for the fractional reactionsubdiffusion equation[J]. Appl Math Comput, 2008, 198(2):754-769.



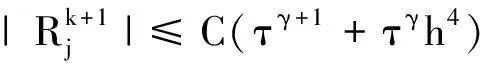
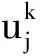


2 隐式差分格式的稳定性分析




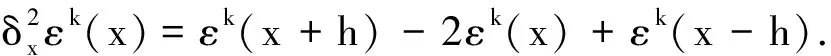


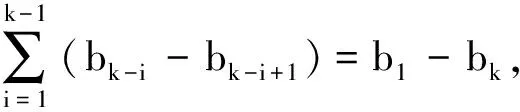
3 数值算例




