阵列波导器件封装高精密运动平台的轴位移研究

阳 波，段吉安，郑 煜

(1.湖南师范大学图像识别与计算机视觉研究所,中国 长沙 410081；2.中南大学机电工程学院, 中国 长沙 410083)

随着半导体制造技术与光MEMS(Optical Micro-Electro-Mechanical System)封装技术的迅速发展，光器件性能越来越稳定、可靠，已经广泛地应用于现代光纤通信领域．波导器件作为光MEMS的核心器件，具有非常广阔应用前景．波导器件封装是利用亚微米精密的运动平台，将入射阵列光纤、波导芯片与出射阵列光纤对准耦合并固结在一起，成为光器件制造的关键技术之一，也是目前光电子器件封装研究的热点问题[1-3]．目前国外实现阵列波导器件封装的单通道功率损耗<0.3 dB，波导与阵列光纤的对准误差<1 μm．下一代阵列波导器件更是提出功率损耗<0.15 dB，平面波导与光纤的对准误差<0.5 μm的性能要求，波导器件封装技术面临严峻的挑战[4-12]．

亚微米精密运动平台通常采用亚微米精密的单一运动机构叠加串联复合而成，如图1(a)所示，平台实现移动重复精密0.2 μm，转动重复精密2 μrad．阵列光纤夹持在运动平台的末端装配架上，波导芯片真空吸附在固定支架上．通过平台的移动和旋转运动，阵列光纤在三维欧氏空间作6自由度亚微米精密的运动并实现与波导芯片的精确对准．

本文通过分析精密运动平台与波导芯片装配平台的坐标变换，在此基础上推导出运动平台、阵列光纤与波导芯片之间运动关系．文章最后对旋转轴的运动与目标原点的位移关系进行仿真．

1 波导器件封装运动平台的设计

1.1 运动平台的设计

刚体在三维欧氏空间中的位姿调整包括位置与姿态的调整[13-15]，为了实现刚体的位姿调整，运动平台通常由3个亚微米精密的移动轴和3个转动轴采用串联叠加的方式复合而成，如图1(a)所示，不考虑装配误差，3个平移轴两两正交．便于讨论，如图1(b)所示分别定义x，y，z3个方向．在x方向轴上再依次串联3个与x，y，z平行的旋转轴，按照平移轴的方法分别定义为δx，δy，δz．在平移轴上内置光栅尺并采用闭环控制，实现平移重复精密达到0.2 μm，而在δx，δy，δz转动轴上实现重复精密2 μrad．

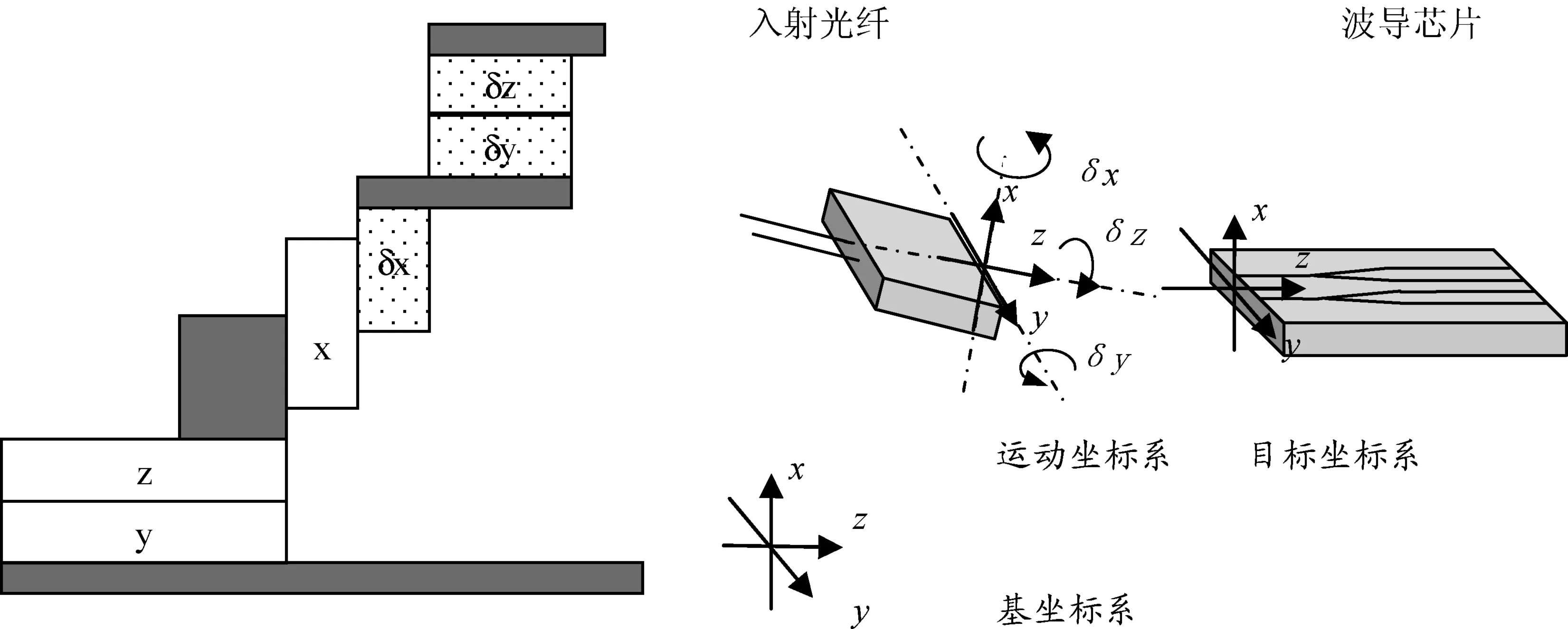
(a) 六轴亚微米精密平台 (b) 坐标系图1 亚微米精密运动平台与空间姿态描述

理想的运动轴任意两轴之间的运动是正交的，但叠加复合平台的各运动轴之间因为运动的原因只有相邻两轴之间相互正交，因此有必要研究运动平台各轴与欧氏空间坐标轴之间的关系．

1.2 波导芯片与阵列光纤装配

图2 波导芯片与阵列光纤对准

为了便于安装阵列光纤，通常在运动平台的最后一级运动机构(z轴)上安装一个装配夹具，装配夹具与z轴运动机构保持水平，阵列光纤固定在装配夹具上．波导芯片非常脆弱，采用真空吸附的方式固定在中间的装配架上，它们的位置关系如图2所示．通过精密运动平台的六轴运动，实现阵列光纤与波导芯片纤芯的高精密对准，最后实现纤芯之间高质量的模场耦合．

2 运动平台的坐标变换

d=[dxdydz]T，δ=[δxδyδz]T,

其中d描述移动运动;δ描述转动运动．

根据运动平台构造方法，把3个移动轴变量记作p=[xyz]T，3个转动轴变量记作θ=[αβγ]T，六维运动列矢量记作P=[xyzαβγ]T．

对于同一坐标系，通常有D≠P，因此有必建立D与P之间的关系：D=F(P).

根据机构运动学的Denavit-Hartenberg方法[13-14]，建立运动的坐标关系表(表1)．

表1 运动平台的各部分的D-H参数

根据D-H方法[14]有

(1)

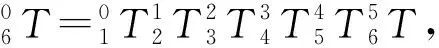
(3)

(4)

(5)

(6)

其中，Cθ=cosθ,Sθ=sinθ，且

px=x+a1+d4′ + (a5′)Cβ+d6′Sβ-a50CβCγ,

考虑实际情况，α，β，γ满足下面的约束条件

式(5)说明运动平台的坐标矩阵姿态与平移轴的参数不相关，只与3个旋转分量相关，式(6)说明坐标原点的运动与各运动轴均有相关．联立式(4)和式(5)得

sinβ=ax,-sinαcosβ=az,-cosβsinγ=ox.

由于n，o，p分别为坐标系的3个单位方向矢量，因此等式的右边均小于或等于1，另外在约束条件(10)条件下有ax<1，因此等式(3)的解存在2种情况：

(1) 当满足下列条件时，

式(3)有唯一解

(7)

代入式(6)便可以求出向量p=[xyz]T．

(2) 其他情况无解，表明运动平台不可达．

3 应用实例与结果分析

根据式(5)和式(7)可以求出运动的姿态和原点的位置矢量．由式(5)可知，原点位置与平移轴的变量线性相关，但与转动轴变量是高度非线性的关系．分别单独驱动旋转轴，对运动坐标系的原点在参考坐标系的位置进行数值仿真实验，运动平台平移的位移单位为μm，转动轴的转动单位是μrad，平移精密为0.2 μm，转动重复精密2 μrad，设定初始位置P0=[40 000 20 000 200 000 50 000 -50 000 50 000]T，分别假设3个转动轴的匀速转动，速度是1 700 μrad/s(近似0.1 °/s)，得到原点投影在参考基坐标系3个轴上的运动轨迹，如图3所示．

(a) α匀速转动，β，γ不动

(b) 匀速转动，α，γ不动

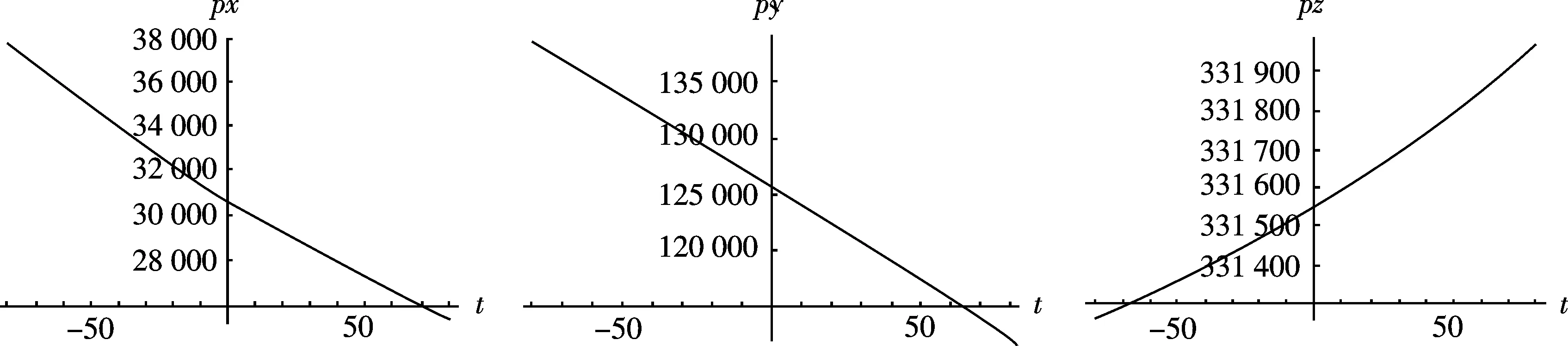
(c) γ匀速转动，α，β不动图3 单独转动轴运动对原点位置的影响比较

从运动轨迹上不难发现，角度的变换对原点位置的影响非常大，且相对于基坐标系各个轴的运动轨迹不相同．

4 结论

通过对微精密运动平台坐标的变换研究发现，采用正交叠加串联的运动平台，刚体的空间姿态只与3个转动轴相关，与3个平移轴无关．在实际机构设计中，3个转动机构的变量在正负10°范围内，运动反解的求解是确定的．但是原点的位置与平移轴和转动轴相关，且与3个转动变量是非常复杂的非线性关系．

然而在实际制造和装配过程，严格意义上的正交条件是很难做到的，有必要开展近似正交的机构运动关系和精密控制研究．

参考文献：

[1] ZHANG R. Study of novel algorithms for fiber-optic alignment and packaging automation[D]. Irvine: University of California, 2003.

[2] MURAKAWA M, NOSATO H, HIGUCHI T. Automatic optical fiber alignment system using genetic algorithms[J]. Artif Evol, 2004, 936:129-140.

[3] 刘洪举,刘大伟.集成光学条波导阵列与单模光纤阵列的联结[J].光子学报, 1997,26(7):1313-1317.

[4] 帅词俊,段吉安,王 炯,等.光纤耦合器熔融拉锥粘弹性建模与分析[J].中南大学学报：自然科学版，2006,37(1):79-83.

[5] 沙慧军,陈抱雪.光波导-光纤耦合对接自动化系统的研究[J].光子学报,2005,34(12):1773-1777.

[6] ZHANG Z Y, LIU J R, ZHAO P,etal.Active alignment of optical fibers to planar waveguides using a thermal-curing adhesive [J].J Light Tech, 2005,23(2):567-570.

[7] LING Y, HUANG H, CHEN W K ,etal. Polishing of fiber optic connectors [J]. Mach Tool Manu,2004, 44:659.

[8] JEONG S H, KIMB G H, CHAC K R. A study on optical device alignment system using ultra precision multi-axis stage[J]. J Mate Proc Techno,2007,65:187-188.

[9] KIM J Y, LEE B R, YANG S Y,etal. Precision position control of piezoactuator using inverse hysteresis model and euro-PID controller[J]. Contr Auto Syst Eng, 2003, 9-11:22-29.

[10] 宋金声.我国光无源器件的技术发展合发展趋势[J].世界宽带网络, 2002, 9(11): 16-18.

[11] HSIEH C H, WU T L, CHENG W H. An optimum approach for fabrication of low loss fused fiber couplers[J]. Mater Chem Phys, 2001, 69(7):199-203.

[12] 刘景琳,段吉安,苗健宇,等. 熔融拉锥型光纤耦合器实验研究[J].中南大学学报：自然科学版. 2006,37(1):103-107.

[13] DENAVIT J, HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. J Appl Mech,1995,21(5):215-221.

[14] DING HAND. Computer-aided off-line planning of robot motion[J]. Robo Auto Sys,1991,7(1):67-72.

[15] KIM J Y, LEE B R, YANG S Y,etal. Precision position control of piezoactuator using inverse hysteresis model and euro-PID controller[J].Contr Auto Syst Eng, 2003(9):22-29.