一类高阶线性变系数常微分方程的通解

肖建中， 刘佳音

（南京信息工程大学数理学院数学系，南京 210044）

一类高阶线性变系数常微分方程的通解

肖建中， 刘佳音

（南京信息工程大学数理学院数学系，南京 210044）

利用升阶法研究了一类高阶线性变系数常微分方程，给出了齐次方程的通解公式，并讨论了非齐次方程待定的特解.

高阶线性变系数常微分方程；升阶法；通解；特解

我们知道，对于常系数线性微分方程，即使是高阶的，可通过特征方程求齐次方程的通解，可用常数变易法、待定系数法、算子解法、拉普拉斯变换法等方法求特解.但是对于变系数线性微分方程，尤其是高阶的，一般没有确定的解法，求解的基本原则是降阶［1-4］.一般来说，低阶方程的求解比高阶方程的求解要简单些，但不尽然，有时通过对方程求导使方程的阶升高（称为“升阶法”），反而使方程求解变得简单.在非齐次线性微分方程的常系数情形，文［5-7］介绍了求得特解的升阶法，有时确实比待定系数法等方法简单.在线性微分方程的变系数情形，文［8］给出了用升阶法求解的几个例子.下述例子就是文［8］给出的：

求解方程x2y″-2xy′＋2y＝0.对此方程两边关于x求导，得x2y‴＝0，即y‴＝0.由此得y＝c0＋c1x＋c2x2，代入原方程，得c0＝0，故原方程的通解为y＝c1x＋c2x2.

受此例的启发，本文探求可用升阶法简便求解的高阶线性变系数微分方程类.分析上述例子的系数函数间关系，一个自然的问题是：下述一般形式的方程（p（x）≠0）.

用升阶法是否可解？

本文给予此问题明确的回答.对方程（1）给出了求解公式；对方程（2）相应于f（x）的不同情形讨论了特解的待定形式.由于方程（2）是线性的，故方程（2）的通解可表示为方程（1）的通解与方程（2）的特解之和，从而方程（2）的通解可求出.本文最后给出了所得结果的一些应用实例.

以下记L［y］＝p（x）y（n）＋（-1）1p′（x）y（n-1）＋…＋（-1）np（n）（x）y，方程（1）即L［y］＝0，方程（2）即L［y］＝f（x）.

（a）若β＝0，则方程（1）的通解为

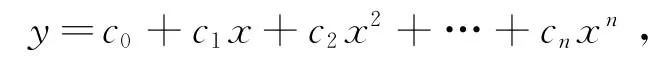
这里ci（i＝0，1，…，n）为n＋1个常数，其中n个是任意的.

（a）若αn＋1-（-β）n＋1≠0，则方程（2）有形如y（x）＝Qm（x）eαx＋Cy0（x）的特解，其中Qm（x）为待定的次数不超过m的多项式，C为待定的常数.

（b）若α为λn＋1-（-β）n＋1＝0的j重根（j≥1），则方程（2）有形如y（x）＝xjQm（x）eαx＋Cy0（x）的特解，其中Qm（x）为待定的次数不超过m的多项式，C为待定的常数.

证对方程（1）两边关于x求导，得到方程（2）的升阶方程为

现考察方程（2）的解与方程（7）的解之间的关系.显然方程（2）的具有n＋1阶导数的解必是方程（7）的解.设y＝h（x）是方程（7）的解，则p（x）h（n＋1）（x）＋（-1）np（n＋1）（x）h（x）＝f′（x），对此式取从x0到x的积分（x0为p，f，h公共定义域中某固定的点），有

方程（8）为非齐次的常系数线性微分方程，由特解理论［4］，若αn＋1-（-β）n＋1≠0，则方程（8）有形如y1（x）＝Qm（x）eαx的特解；若α为λn＋1-（-β）n＋1＝0的j重根（j≥1），则方程（8）有形如y1（x）＝xjQm（x）eαx的特解.于是根据方程（2）的解与方程（7）的解之间的关系得到（a）与（b）.

实际求解中，可采用先求方程（2）的升阶方程的通解再代入方程（2）确定一个常数的方法.

［1］ 丁同仁，李承志.常微分方程教程［M］.北京：高等教育出版社，1998.

［2］ 叶彦谦.常微分方程讲义［M］.2版.北京：人民教育出版社，1982.

［3］ 王柔怀，伍卓群.常微分方程讲义［M］.北京：人民教育出版社，1963.

［4］ 东北师范大学数学系.常微分方程［M］.2版.北京：高等教育出版社，2005.

［5］ 朱灵.用升阶法求常系数非齐次线性微分方程的特解［J］.高等数学研究，2002，5（2）：17-19.

［6］ 李青，徐崇志，胡汉涛.用升阶法求常系数非齐次线性微分方程的特解［J］.塔里木农垦大学学报，2003，15（1）：24-25，57.

［7］ 梅宏.常系数非齐次线性微分方程特解的一种求法——升阶法［J］.高等数学研究，2003，6（2）：22-23，47.

［8］ 屈英.一类常微分方程的解法［J］.高等函授学报，1999，12（1）：13-14.

The General Solutions of aclass of Higher-Order Linear Ordinary Differential Equations with Variable Coefficients

XIAO Jian-zhong， LIU Jia-yin
（Department of Mathematics，Nanjing University of Information Science and Technology，Nanjing 210044，China）

aclass of higher-order linear ordinary differential equations with variable coefficients are studied by means of the order-increasing methods.The general solutions of homogeneous equations are given and the undetermined particular solutions of non-homogeneous equations are discussed.

higher-order linear ordinary differential equations with variable coefficients；order-increasing methods；general solution；particular solution

O175.1

C

1672-1454（2011）04-0182-04

2008-10-08

南京信息工程大学课程建设项目（JG032006J01）