改进ICA的人脸特征提取方法

杨颖娴

(广东司法警官职业学院信息管理系，广东 广州 510520)

改进ICA的人脸特征提取方法

杨颖娴

(广东司法警官职业学院信息管理系，广东 广州 510520)

在人脸特征提取的过程中主要采用ICA方法。介绍了ICA算法的原理，并对ICA算法的优缺点进行了讨论，给出了改进的ICA算法。试验结果表明，改进的ICA算法应用于人脸的特征提取比PCA算法更具有优越性，所提取的人脸特征更利于人脸的分类，从而获得较高的识别率。

独立元分析法；特征提取；人脸识别

近年来，人脸识别的研究已经成为生物识别和人工智能领域的一个研究热点，得到了越来越多的关注。由于人脸识别与其他生物特征识别相比具有更直接、无侵犯性、隐蔽性、采集设备便宜等优势，所以该项技术已被广泛地应用于公安、智能门禁、交通流量控制、智能视频监控、银行卡持卡人身份验证、ATM识别认证、司机驾照验证、医学、视频会议、人机交互系统等各方面。特征提取是人脸识别中一个非常重要的环节，目的是为了降低人脸图像的维数。目前，常用的基于统计的特征提取方法有主成分分析(PCA)[1]和线性判别分析(LDA)[2]等。独立元分析(ICA)[3]是近年来发展起来的一种新的多维数字信号处理技术，其基本思想是在最大程度保持信息量的前提下，从高维数据空间中提取出低维数据的特征分量，是一种基于人脸全局特征的识别方法。相比较于PCA算法，ICA算法的思想是获取数据的独立分量，是一种基于人脸局部特征的识别方法，并且考虑了传统的PCA未考虑信号的高阶统计特性，去除了信号中高阶冗余信息。但ICA算法在获取独立分量的过程中需要获取人脸图像的先验知识，这影响了识别的准确率。P.C.Yuenet[4]针对ICA算法的不足，利用类内距离均值和类间距离均值获取独立分量，取得了较好的效果。笔者在此基础上采用小波变换对输入的人脸图像进行降维，再利用改进的ICA方法获取独立分量，有效减少了后续工作的计算量，取得了较高的识别率。

1 基于ICA的人脸识别

ICA作为一种盲源信号分离技术[5]，是基于信号的高阶统计特性的分析方法。由原始样本数据求一个特征空间，然后把新的数据映射到这个特征空间，获得一组特征向量，用来分类识别。ICA算法要求各个分量间是统计独立的，其独立性由概率密度来定义。如果2个随机变量是独立的，当且仅当联合概率密度为：

p(y1,y2)=p1(y1)p2(y2)

(1)

式中,p1(y1),p2(y2)是y1、y2概率密度分布函数;p(y1,y2)是y1、y2的联合概率密度分布函数。

由式(1)，定义连续型随机变量f(x)的数学期望：

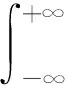
对独立随机变量可以衍生如下重要特性，对任意2个连续型随机变量f1和f2，如果f1，f2独立，总有：

E{f1(y1)f2(y2)}=E{f1(y1)}E{f2(y2)}

(2)

将独立元分析应用于人脸识别时，上述独立随机变量就是训练人脸的特征向量。

记xi为1幅人脸数据，可以构造一个训练人脸集合{x1,x2,…,xm}(xi表示一幅m×n大小的人脸图像按列展开成的mn维向量)，其中每个人脸数据看作是n个独立元素s1,s2,…,sn的线性组合，这些独立元素是互相概率独立的并具有零均值。将观察变量xi记做向量X,X={x1,x2,…,xm)T，将元素si记做向量S,S=(s1,s2,…sn)T。S与X的关系表述如下：

X=AS

(3)

式中，A是一个满秩的m×n的矩阵；si表示观察值xi的第i个特征的幅值。如果独立元素si满足E{sisi}=1(i=1,2,…,n)，那么独立元素将是除符号外唯一的。

ICA方法的基本目标是寻找一个线性变换称之为分离矩阵W，使得：

Y=WAS

(4)

可见输出的人脸数据向量Y是独立统计分量S的一个估计，当分离矩阵W是A的一个逆矩阵时，S在Y中得到了分离。则训练样本集X在独立基子空间上的投影为U=SXT,任何输入人脸图像可以通过独立基重建。计算出Y以后，特征空间可以由Y的行向量构造，把每一张待测试的人脸图像映射到这个特征空间，得到一组系数向量用于识别。

在实际应用中，上述方法往往受到一些限制。因为A、S都是未知的，虽然可以根据输出信号的独立性原则来有效地估计A、S，但由于没有任何参照目标，上述过程是无监督、无组织的过程。其次，令P=WA，则P可用来衡量ICA算法的分离性能，当P=I时，估计的性能最理想，但由于缺少独立信号源的先验知识，P化为单位矩阵的过程往往会遇到困难。

2 改进的ICA算法

由于分离矩阵W的计算存在困难，可通过输入人脸图像的类内距离均值和类间距离均值的比值来控制独立特征之间的差别性。

记X的i行、j列为aij。记j列的类内距离均值为Wj[5]：

(5)

记j列的类间距离均值为Bj，则：

(6)

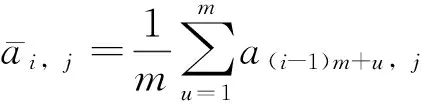
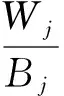
(7)

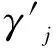
小波变换通过对预处理过的人脸图像进行降维，可提取人脸全局特征，因而将小波变换和改进的ICA算法相融合来进行人脸特征的提取。首先利用小波变换对人脸图像进行降维，这样可以有效消除噪声且减少运算量，然后利用改进的ICA算法获取人脸图像的独立特征子空间。

3 实例分析

3.1人脸图像的预处理

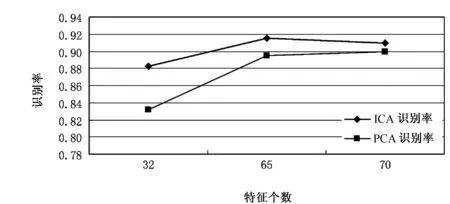
图2 PCA、改进ICA方法识别率的比较

现实的人脸识别中，样本经常受到噪声的影响，会出现重叠或离群的情况，而且人脸图像中的头发、衣服和背景等的像素灰度值也会影响到人脸特征提取。为此, 对输入的人脸图像进行预处理是人脸识别系统的前期工作。首先需要把彩色图像转变为灰度图像，采用列像素灰度值之和的直方图寻找人脸的左右边界，然后采用行像素灰度值之和的直方图寻找人脸的上下边界，再利用直方图均衡化方法对人脸图像进行灰度归一化，从而有效消除噪声对人脸图像灰度分布的影响。

3.2在ORL人脸库上的对比试验

英国ORL人脸图像库是目前使用最广泛的人脸数据库，笔者所做试验都是基于该数据库进行测试。该图像库由40人、每人10幅112×92图像组成，不仅人的脸部表情和脸部细节有着不同程度的变化，而且人脸姿态也有相当程度的变化。根据不同视角、表情、不同的人脸细节，选择该图像库中10人，每人选择前3幅为训练集，另7幅作为测试集，样本集和测试集分别包含30张和70张人脸。PCA、改进ICA方法识别率的比较如图2所示。从图2可以看出，随着独立分量个数的增加，改进ICA方法比PCA方法的识别率更高。这是由于独立分量数越多，样本投影到的独立子空间的基向量也越多，特征分量间的高阶冗余度越小。上述测试表明，利用改进ICA方法进行人脸的特征提取比PCA算法更具有优越性，其获得的特征子空间更利于人脸的分类。

4 结 语

阐述了ICA方法的相关理论，并利用独立元分析提取人脸特征。在人脸图像的预处理阶段，利用小波变换保留人脸识别的大部分有用信息，可大大降低人脸数据的维数，而改进的ICA算法利用类内距离均值和类间距离均值获取独立分量，不再需要获取人脸图像的先验知识，可使运算的复杂度降低。因此，提取的人脸特征更利于人脸的分类，从而获得较高的识别率。

[1]余晓梅，徐丹.基于外观的子空间人脸识别方法研究[J].计算机应用研究，2007，24(5)：10-12.

[2]Belhumeur P N，Hespanha J P，Kriengman D J.Fishedaces lRecognition using class specific linear projection[J].IEEE Transaction on Pattern Analysis and MachineIntelligence，1997，19(7)：771-720.

[3]张贤达，保铮.盲信号分离[J].电子学报，2001，29(12)：1767-1771.

[4]Yuenet P C. Face representation using independent component analysis[J].Pattern Recognition, 2002，35(6):1247-1257.

[5]Bell A J.An information maximization approach to blind separation and blinddeconvolution[J].Neural computation，1995，7(6)：l129-l131.

[编辑] 李启栋

10.3969/j.issn.1673-1409.2011.05.030

TP391.4

A

1673-1409(2011)05-0088-03