利用沃尔公式确定原始含油饱和度的方法

刘 洁, 包世界

(长江大学地球科学学院，湖北 荆州 434023)

包 婷

(北京侏罗纪软件股份有限公司，北京 100083)

李映艳

(长江大学地球科学学院，湖北 荆州 434023)

涂杰勇

(北京侏罗纪软件股份有限公司，北京 100083)

龚 敏

(中石油冀东油田分公司，河北 唐山 063501)

利用沃尔公式确定原始含油饱和度的方法

刘 洁, 包世界

(长江大学地球科学学院，湖北 荆州 434023)

包 婷

(北京侏罗纪软件股份有限公司，北京 100083)

李映艳

(长江大学地球科学学院，湖北 荆州 434023)

涂杰勇

(北京侏罗纪软件股份有限公司，北京 100083)

龚 敏

(中石油冀东油田分公司，河北 唐山 063501)

评价储层的重要指标之一就是储层的原始含油饱和度。以平均毛管压力曲线为基础，探讨了采用沃尔公式法确定储油层油的最小流动孔喉半径，从而确定油的最大含油饱和度的方法，并结合中国某油藏的实际压汞资料数据，详细介绍该方法的实施过程。实例分析表明，该方法能够有效地计算该地区的原始含油饱和度。

毛管压力曲线；原始含油饱和度；J函数；沃尔公式

油藏的原始含油饱和度是指原始条件下储集层中油的体积占有效孔隙体积的百分比。确定油藏原始含油饱和度的方法很多，例如岩心直接测定方法、测井解释法和毛管压力曲线计算方法等。下面，笔者在研究各种已有方法的基础上，结合研究区的地质背景条件，选择利用沃尔公式确定研究区的原始含油饱和度。

1 原始含油饱和度的求取

1.1平均毛管压力曲线的计算原理

因为汞不润湿岩石，可作为非润湿相，因此可以用压汞法(即在高压条件下把汞压入岩石样品中)求出与之平衡的毛管压力和压入汞的体积，得到毛管压力和岩样的含汞饱和度关系(即岩样的毛管压力曲线)。

利用J函数处理是获得平均毛管压力资料的经典方法。J函数是一个无因次量,是关于岩心的标准化饱和度SwD的函数，J函数和毛管压力Pc的关系式[1]如下：

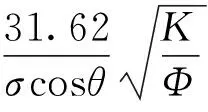
(1)

式中，σ为界面张力，mN/m；K为渗透率，μm2；Φ为孔隙度；Pc为毛管压力，MPa；θ为润湿角，(°)。

对于有压汞法测试的毛管压力曲线，汞和空气的界面张力σ=480mN/m，汞的润湿角θ=140°，因此J函数可以表示为：

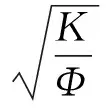
(2)

不同岩样的J函数与岩心的标准化饱和度SwD之间存在如下指数关系[1]：

(3)

不同的岩样具有不同的a、b值。岩心的标准化饱和度SwD表示了岩样在所有压力点下的汞饱和度SHg的最大值max(SHg)与其在每个压力点下的SHg之差除以max(SHg)：

(4)

定义Swi为岩样的束缚水饱和度：

Swi=1-max(SHg)

由式(2)、式(3)以及岩心的标准化饱和度SwD可以得到毛管压力Pc与汞饱和度SHg的关系：

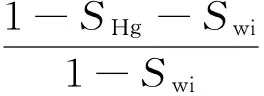
(5)

对所有的样本计算常数a、b、Φ、K和Swi的算术平均或几何平均，从而建立具有代表性的平均毛管压力与汞饱和度的关系曲线[1-4]：

(6)

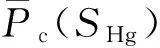
(7)

因为实验室条件下(空气-汞系统)的界面张力σL=480mN/m，接触角θL=140°；地层条件下(油-水系统)的界面张力σR=30mN/m，接触角θR=30°，可知将实验室内平均毛管压力(Pc)L换算为油藏条件下毛管压力(Pc)R的换算系数是0.070657。所以油藏条件下的平均毛管压力曲线为：

(8)

1.2利用沃尔公式法求原始最大含油饱和度

在获得平均毛管压力曲线的基础上，采用沃尔公式法，可以计算出储层油的最小流动孔喉半径。沃尔公式法是以等孔隙体积增量为基础，计算每一个孔隙体积间隔中的渗透能力贡献值ΔKi及累积渗透能力ΣK，当最终累积渗透能力ΣK达到99.9%时，所对应的孔喉半径就是最小流动孔喉半径，同时对应的进汞饱和度即为该区的原始最大含油饱和度。

沃尔公式法如下：

(9)

式中,ri表示相应的孔隙半径。沃尔公式法的计算步骤如下：

1)设定汞饱和度SHg的计算起始值为零，确定取值步长step(如step=0.02)。

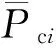
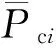
(10)

油藏条件下，半径ri可表示为：

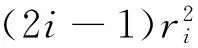
5)按式(9)计算第i个节点对应的区间渗透能力贡献值ΣKi以及对应的累积渗透能力ΣK，直到ΣK=100%为止。

6)从步骤5)求出的结果中找到第1个满足ΣK≥99.9%的ΣK值，则该值所对应的ri即为油的最小流动孔喉半径，对应的SHgi即为所求的最大原始含油饱和度。

2 实例分析

根据以上算法分析编制了计算机程序。以中国某油藏毛管压力曲线的实际处理以及用沃尔公式法确定最大含油饱和度的过程进行实例应用。

研究数据包括5块岩样在不同压汞毛管压力下的汞饱和度和压汞综合数据,如表1所示。由于数据量较大，5块岩样在30个压力点对应的汞饱和度，在此不列出具体数值。5块岩样的毛管压力曲线如图1所示。

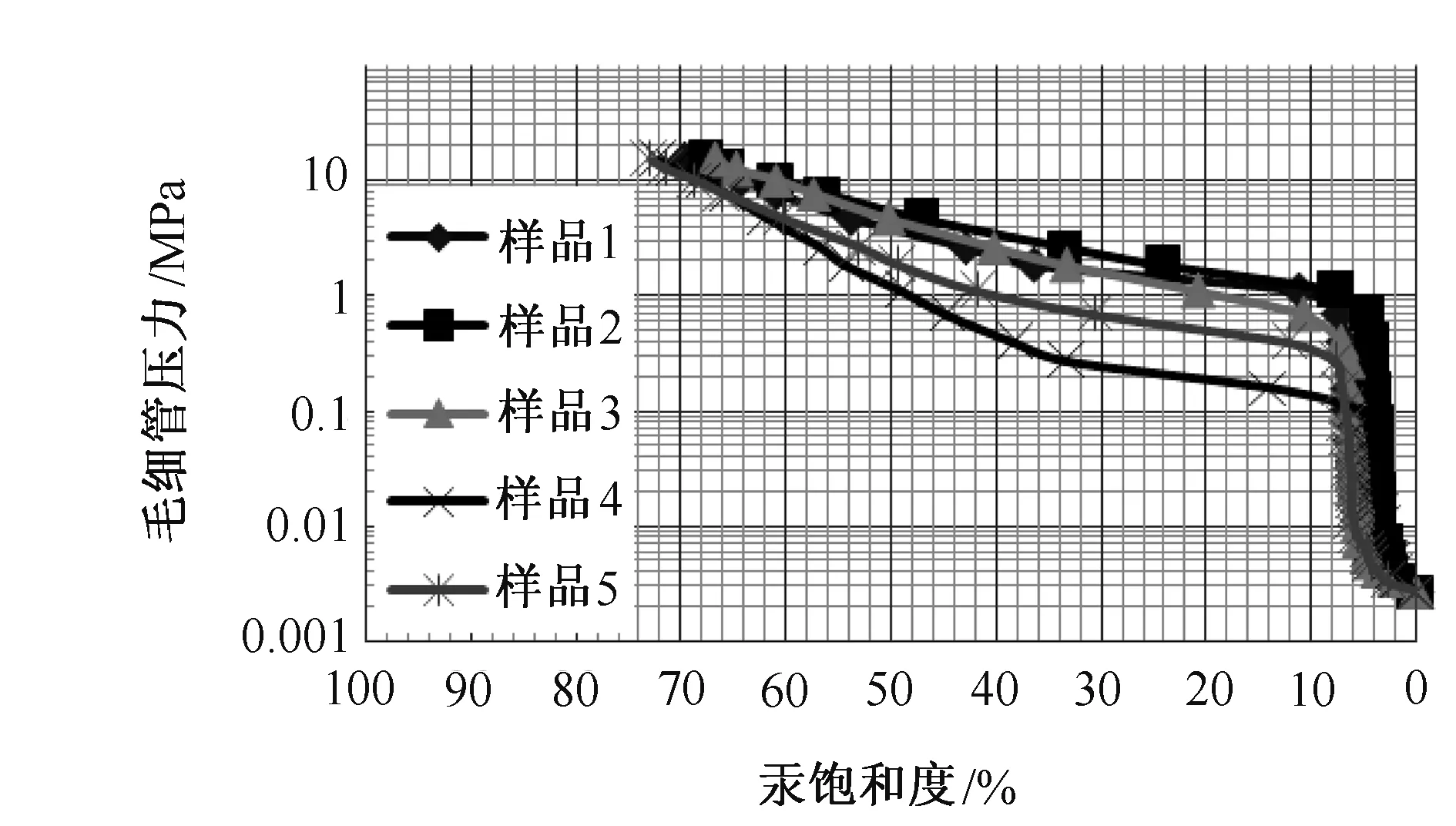
图1 5个样品的毛管压力曲线

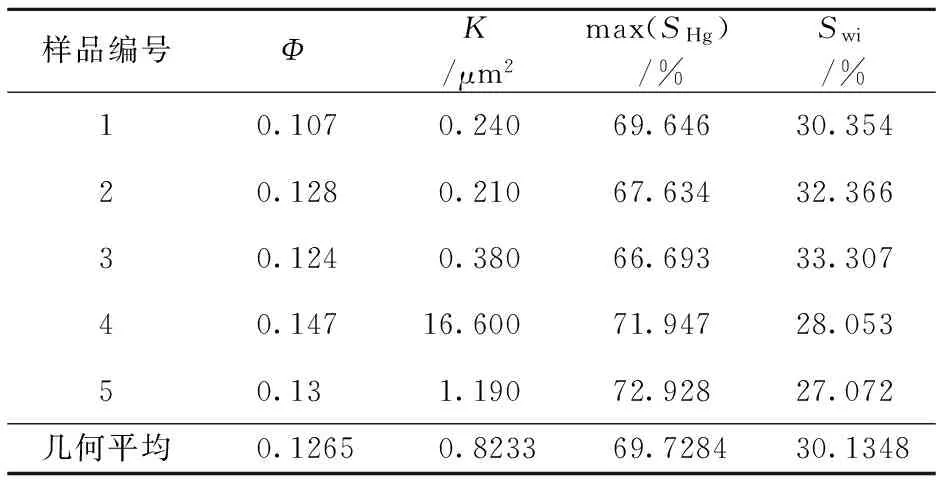
样品编号ΦK/μm2max(SHg)/%Swi/%10.1070.24069.64630.35420.1280.21067.63432.36630.1240.38066.69333.30740.14716.60071.94728.05350.131.19072.92827.072几何平均0.12650.823369.728430.1348

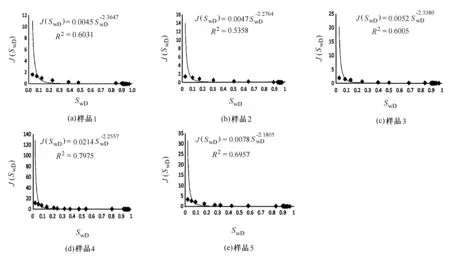
图2 各样品的J函数拟合

样品编号a(a)b(b)10.0045-2.364720.0047-2.276430.0052-2.33840.0214-2.255750.0078-2.1805算数平均0.0087-2.2831

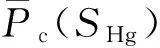
将孔喉半径和累积渗透能力随汞饱和度的增加的变化情况绘制于图4，图中虚线标记为最终累积渗透能力∑K达到99.9%，此时对应的孔喉半径为该储层油的最小流动孔喉半径，为0.63μm，对应的汞饱和度即为该储层的最大原始含油饱和度，为54%。

图3 实验室及油藏平均毛管压力曲线 图4 累积渗透能力和孔喉半径随SHg的变化趋势

[1]陈元千，李璗.现代油藏工程[M].北京:石油工业出版社，2004：55-62.

[2] 廖敬等.毛管压力曲线平均化及J函数处理[J].特种油气藏，2008，15(6)：73-75.

[3] 缪志伟.一种计算平均毛管压力曲线的方法[J].新疆石油地质，1997，18(1)：67-69.

[4] 罗明高.毛管压力曲线分布特征的确定[J].西南石油学院学报，1988，10(4)：71-85.

[5] 唐衔等.利用压汞曲线求取油藏原始含油饱和度的研究[J].重庆科技学院学报，2008(5)：23-26.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.05.017

P618.13

A

1673-1409(2011)05-0052-03