基于遗传算法的威布尔溶出曲线参数估算方法研究Δ
陈天朝,赵新红,康冰亚(.河南中医学院第一附属医院中药制剂国家局三级实验室,郑州市450000;.河南中医学院,郑州市 450008)
基于遗传算法的威布尔溶出曲线参数估算方法研究Δ
陈天朝1*,赵新红2,康冰亚1(1.河南中医学院第一附属医院中药制剂国家局三级实验室,郑州市450000;2.河南中医学院,郑州市 450008)
目的:利用遗传算法全局搜索能力的优势,进行威布尔溶出曲线参数估算。方法:以通脉丸中竹节香附素A的溶出数据为研究载体,利用Matlab软件中遗传算法优化工具箱实现威布尔溶出曲线参数估算,并与非线性最小二乘法估算结果进行统计学比较。结果:遗传算法与非线性最小二乘法估算的威布尔溶出曲线参数无显著性差异(P>0.05),而遗传算法估算参数的校正均方差小于非线性最小二乘法。结论:遗传算法适用于威布尔溶出曲线参数的估算。
遗传算法;威布尔溶出曲线参数;非线性最小二乘法
对溶出数据的处理,特别是非线性溶出曲线参数估算是研究固体制剂溶出度的重要内容之一。随着信息技术的发展,各种拟合理论及优秀的统计学软件能够完成这项工作,如林鸿彬[1]借助于遗传算法全局搜索策略、优化时不依赖于梯度信息以及解决非线性问题的鲁棒性的优点来实现复杂的非线性数据拟合。本文以笔者研究的通脉丸中竹节香附素A的溶出数据为载体,尝试借助Matlab软件中遗传算法优化工具箱(Genetic Algorithm Optimization Toolbox,GAOT)对威布尔溶出曲线进行拟合并估算参数,旨在丰富溶出曲线拟合处理方法,为药学工作者更好地进行溶出数据处理及分析提供参考。
1 仪器与材料
1.1 仪器
ZRS-8C型智能溶出试验仪(天津大学无线电厂);E2695型高效液相色谱仪(美国Waters公司)。
1.2 材料
通脉丸(河南中医学院第一附属医院中药制剂国家局三级实验室提供,批号:101128,规格:每袋5g,系由两头尖等11味中药制成的蜜丸)。
Matlab R2010a软件(美国Math Works公司)。
2 方法
2.1 溶出数据
通脉丸中竹节香附素A在不同时间的累积溶出百分率如表1所示。

表1 竹节香附素A在不同时间的累积溶出百分率实测值Tab 1 Accumulative dissolution percentage of raddeanin A at different time
2.2 遗传算法基本原理
遗传算法(GeneticAlgorithm,GA)是基于达尔文进化论和孟德尔遗传学说的一种随机搜索算法,通过随机产生一群初始解,根据适者生存的原则,从中选择出适应环境的个体进行复制,并经过交叉、变异2种基本操作产生新一代更适合环境的群体,最终收敛获得最优个体,从而得到问题的最优解[2,3]。
笔者首先应用Matlab语言编写目标函数文件Weibull.m,并将文件存放在工作目录下,程序如下:

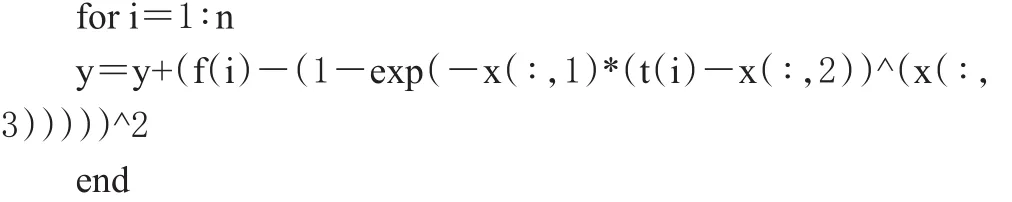
2.3 遗传算法与非线性最小二乘法(Nonlinear Least Squares Method,NLLS法)估算威布尔溶出曲线参数及比较
2.3.1 遗传算法。设定威布尔溶出曲线为f=1-exp(-b*(t-a)^m)(f为累积溶出百分率,t为溶出时间,a为溶出时滞值,b为尺度参数,m为形状参数),首先在Matlab R2010a软件中的遗传算法优化工具箱中进行遗传算法参数优选[1],经过对多种参数进行组合试验,最终确定了以下参数设置:“Fitting function”窗格中输入“@Weibull”,“Number of variable”窗格中输入“3”。在“Lower”与“Upper”窗格中分别输入威布尔溶出曲线参数的约束条件:“[000]”与“[0.11.51]”。“Options”项下的“Population Size”窗格设定为“100”,以轮盘赌选择法(Roulette)进行随机选择,应用单点交叉法且交叉概率为0.7进行交叉操作,最终以变异概率0.07进行变异,其他参数均为缺省值。
2.3.2 NLLS法。为了评价遗传算法对威布尔溶出曲线参数估算的优良性,选择NLLS法进行溶出曲线参数估算,借助Matlab曲线拟合工具箱[4](Curve Fitting Toolbox,CFT)实现威布尔溶出曲线参数估算。
比较2种方法所得威布尔溶出曲线参数结果及其校正均方差(Root Mean Square Error of Calibration,RMSEC),并通过与实测值比较2种方法的一致性。
3 结果
3.1 2种方法威布尔溶出曲线参数估算比较
由于遗传算法中的初始个体是在取值域中随机产生的,使得每次得到的初值群体并不完全相同,因此按照“2.3.1”项下的方法,重复操作5次来估算溶出曲线参数,结果显示遗传算法对于不同的初始群体均能够收敛得到最优解。通过比较2种方法对威布尔溶出曲线参数估算结果,经统计分析发现2种拟合方法获得的3个溶出曲线参数均无显著性差异(P=0.955>0.05)。对2种方法拟合的溶出曲线参数的RMSEC比较可知,遗传算法拟合的RMSEC小于NLLS法,表明遗传算法可以应用于溶出曲线参数拟合。2种方法最终估算结果见表2。
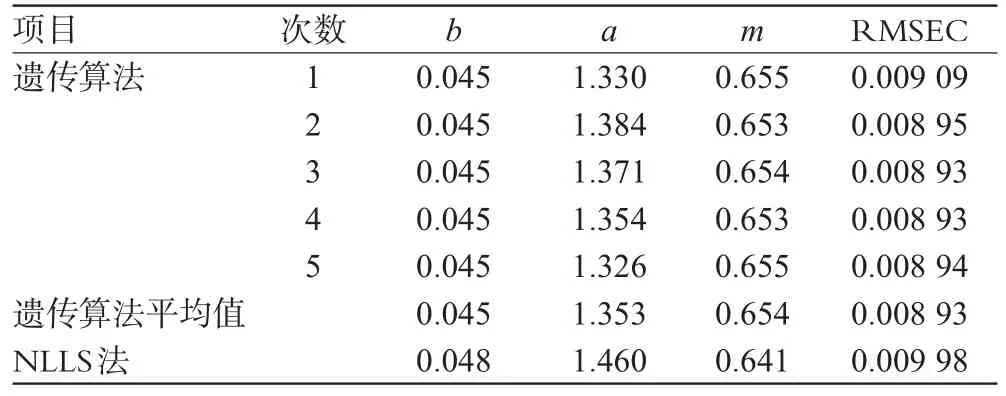
表2 2种方法威布尔溶出曲线参数拟合值Tab 2 Fitted Weibull dissolution curve parameters by 2kinds of methods
3.2 2种拟合方法的预测效果比较
以表2中2种方法拟合的威布尔溶出曲线参数为依据,推算累积溶出百分率;通过对2种拟合方法预测的累积溶出百分率进行单因素方差分析,可知2种拟合方法预测的累积溶出百分率无显著性差异(P=0.979>0.05),详见表3。
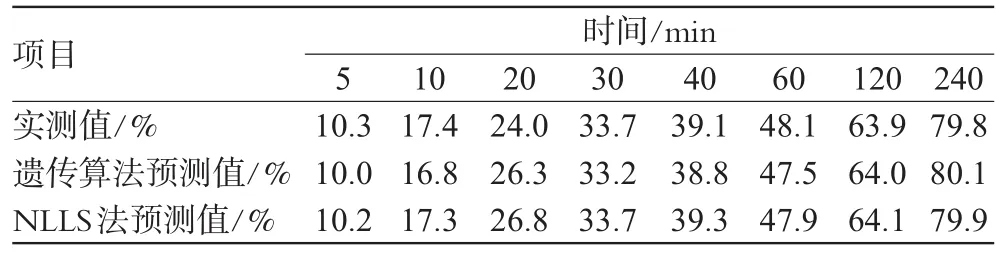
表3 2种方法估算的累积溶出百分率与实测值比较Tab 3 Comparison of accumulative dissolution percentage and measured value by two methods
3.3 2种方法拟合图谱
将实测值与2种方法拟合值绘制散点图及拟合曲线图,由拟合效果图可知2种拟合方法所得结果均呈现出良好的一致性,详见图1。

图1 2种方法拟合值及实测值散点图Fig 1 Scatter plot of fitted value and measured value by two methods
4 讨论
4.1 威布尔溶出曲线参数约束条件的选择
在威布尔溶出曲线中,a为位置参数,在溶出研究中一般为正值或零,正值表示有时间延迟;m为形状参数,其决定了拟合曲线的形状;b为尺度参数[5]。由于溶出数据中第1次取样时间为5min,同时结合NLLS法估算的参数结果,为了减少遗传算法的搜索时间,同时提高搜索精度以及避免出现拟合结果不符合实际情况,最终确定了3个威布尔溶出曲线参数的取值范围。
4.2 遗传算法与NLLS法比较
NLLS法是从单一初始值来进行迭代产生1个单点,通过梯度变化量来求解最优解,存在容易误入局部最优点的不足之处。而遗传算法是以目标函数为依据,不依赖于梯度信息,从串集开始全面搜索,且每次迭代产生1个种群,种群经过选择、交叉、变异等随机过程来实现基因重组和基因突变,最终获得最优解,从而避免出现局部最优的不足之处。然而,遗传算法存在着数学理论较深、最初的参数值的设置复杂等不足之处。因此,应用遗传算法进行参数估算时,需要借助于其他计算工具获得初步结果,再进行参数设置,这使得该算法在参数估算方面受到限制,尤其是无其他计算工具时。
4.3 Matlab遗传算法优化工具箱的优势
Matlab软件中自带各种工具箱,如GAOT、CFT、Statistic Toolbox等,这些工具箱将成为各种曲线拟合运算以及最终结果可视化的强有力工具。本文中应用的GAOT与CFT相比,两者最大的区别在于GAOT是专门为实现遗传算法而设计的工具箱,仅需要对工具箱中的若干参数进行选择与设置,就完全可以方便地完成各种曲线的拟合以及曲线参数优化;而CFT则是基于NLLS法而设计的曲线拟合工具箱,其是借助于NLLS法来实现数学模型的拟合,两者是基于不同的算法来实现曲线拟合的。然而,GAOT对于Matlab软件初学者大大降低了编写复杂的遗传算法程序的难度,同时与CFT估算得到的参数无显著性差异(P=0.955>0.05)。因此,GAOT可以方便地用于药物溶出曲线拟合,具有广泛的实用性。
遗传算法不仅可以用于威布尔溶出曲线拟合,对于其他溶出曲线以及一般非线性模型,仅仅需要选择适当的目标函数,通过对遗传算法优化工具箱中的若干参数进行选择即可完成[6]。通过选择遗传算法与NLLS法来进行威布尔溶出曲线参数估算,试验拟合结果表明了采用Matlab软件中的遗传算法优化工具箱进行威布尔溶出曲线参数具有准确性高、较快的收敛速度及较高的收敛精度的优点。实践证明,遗传算法可以用于威布尔溶出曲线拟合并估算参数,其丰富了药物溶出模型的拟合方法,为药学工作者进行药物溶出模型的拟合提供了参考依据。
[1] 林鸿彬.基于遗传算法的数据拟合在MATLAB环境中的实现[J].湖南农机,2010,37(3):92.
[2] 张善文,刘建度,韩小斌.基于遗传算法的一种数据拟合方法[J].空军工程大学学报(自然科学版),2007,8(1):66.
[3] 周正武,丁同梅,田毅红,等.Matlab遗传算法优化工具箱(GAOT)的研究与应用[J].机械研究与应用,2006,19(6):69.
[4] 曹俊涵,郭晓波.用MATLAB曲线拟合工具箱计算药物溶出度 Weibull分布参数[J].药学进展,2006,30(12):556.
[5] 黄 献,刘裕恒.用SPSS拟合药物溶出度Weibull参数[J].中国药房,2006,17(14):1080.
[6] 蔡 钧.基于遗传算法的测量数据拟合[J].扬州大学学报,2002,5(4):59.
Estimation of Weibull Dissolution Curve Parameters Based on Genetic Algorithm
CHEN Tian-chao,KANG Bing-ya(The Three Level Laboratory of State Administration of TCM Preparation,The First Affiliated Hospital of Henan College of TCM,Zhengzhou 450000,China)
ZHAO Xin-hong(Henan College of TCM,Zhengzhou 450008,China)
OBJECTIVE:To estimate the Weibull dissolution curve parameters on the basis of the superiority of Genetic Algorithm,that is of strong searching ability.METHODS:According to the dissolution data of raddeanin A in Tongmai pill,Genetic Algorithm Optimization Toolbox of Matlab software was used to estimate the Weibull curve parameters,and also compared with the Nonlinear Least Squares Method.RESULTS:There was no significant difference of Weibull dissolution curve parameters between Genetic Algorithm and Nonlinear Least Squares Method(P>0.05),but the root mean square error of calibration of Genetic Algorithm was smaller than that of Nonlinear Least Squares Method.CONCLUSION:Genetic Algorithm is suitable to estimate the Weibull dissolution curve parameters.
Genetic Algorithm;Weibull dissolution curve parameters;Nonlinear Least Squares Method
R9-39
A
1001-0408(2011)41-3857-03
Δ河南省教育厅2009年度自然科学研究计划项目(2009A36003);河南省2010年科技发展计划(102102310185)
*主任药师,硕士研究生导师。研究方向:中药剂型。电话:0371-66245342。E-mail:ctc661111@163.com
2011-07-14
2011-08-16)