基于插值理论的非线性矩阵方程

刘 巍 熊慧军 王柏育

（1、长沙学院 信息与计算科学系，湖南 长沙 410003；2、湖南大学 数学与计量经济学院，湖南 长沙 410082）

基于插值理论的非线性矩阵方程

刘 巍1熊慧军1王柏育2

（1、长沙学院 信息与计算科学系，湖南 长沙 410003；2、湖南大学 数学与计量经济学院，湖南 长沙 410082）

本文研究了非线性矩阵方程⊗ ( X BX ) − C )−1A的正定解。我们证明了该矩阵方程在Φ ( n ) = { X |Im⊗ ( X BX ) > C}内存在唯一正定解，构造了相应的迭代求解方法，并在最后给出了相应的数值例子。

非线性矩阵方程；插值理论；正定矩阵

1 引言

本文研究非线性矩阵方程

的正定解，其中B,Q是n×n复正定矩阵，A是mnn复矩阵，C是mnmn复半正定矩阵，Im⊗(XBX)是以XBX为对角元的块对角矩阵。

L.A.Sakhnovich在[1]中考虑了一类插值问题，并将这类插值问题转化为求矩阵方程

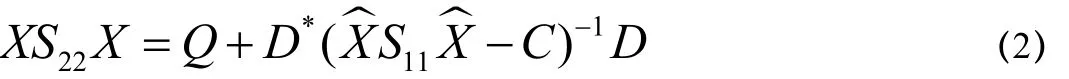
在本文中，我们用 In表示n阶正定矩阵， Cm×n表示m n复矩阵，⊗表示Kronecker积，X表示以X为对角元的m×m块对角矩阵X > 0 (X ≥ 0 )表示X是（半）正定矩阵， X >Y(X ≥Y)表示X−Y是（半）正定矩阵，分别表示n阶全体正定和半正定矩阵的集合。

2 主要结果及证明

我们记Y = XBX，则矩阵方程（1）可写为

引理 1【4】如果 A ∈P(n)，则存在唯一的D∈P(n)，使得A = D2。定理 1【2】如果 A ∈ Cmn×n，Q∈P(n)，C∈P(m n)，且满足，则矩阵方程（3）在内有唯一正定解，且迭代序列收敛到这一正定解。定理2 如果，且满足，则矩阵方程（1）在Φ′(n) ={X|Im⊗(XBX) >C}内有唯一正定解。

证明：由定理1可知，矩阵方程在Φ(n)内有唯一正定解Y，因为B∈P(n)，由引理1，存在唯一的D∈P(n)，使得 B = D2，结合Y = XBX，我们有 ( D XD )2= D YD，由 X ,D,Y ∈P(n)，可知存在唯一的X∈P(n)，使得

考虑迭代

定理3 如果 A ∈ Cmn×n，Q∈P(n)，C∈P(m n)，且满足Ql>C，则迭代序列{Yk}收敛到矩阵方程（3）在Φ(n)内的唯一正定解Y，即收敛到矩阵方程（1）在Φ ′( n)内的唯一正定解

[1]L.A. Sakhnovich, Interpolation Theory and Its Applications, Mathematics and Its Applications, vol. 428, Kluwer Academic,Dordrecht, 1997.

[2]A.C.M.Ran,M.C.B.Reurings.A nonlinear matrix equation connected to interpolation theory. Linear Algebra Appl.,2004, 379:289-302.

[3]Sun Jiguang.Perturbation analysis of the matrix equationA.Linear Algebra Appl.,2003,372:33-51.

[4]Zhang F Z.Matrix theory:basic results and techniques.Springer-Verlag New York Inc,1999.

O241.6, O151.21

A

1673-2219（2011）08-0024-02

2011－04－10

湖南省教育厅基金资助科研项目(09C117). 长沙学院科学研究基金项目(CDJJ-07010204)作者简介：刘巍（1982－），讲师，研究方向为数值代数。

（责任编校：何俊华）