在某些限定条件下的敏感性问题
曾眺英,吕 杰
(华南师范大学数学科学学院,广东广州 510631)
在某些限定条件下的敏感性问题
曾眺英,吕 杰*
(华南师范大学数学科学学院,广东广州 510631)
探讨了拓扑动力系统在对轨道时间集和历经集附加某些限定条件下的敏感性问题,给出了有关此类敏感性的几个基本性质.
-n-初值敏感;初值敏感集;传递点
称(X,T)是一个拓扑动力系统(简称动力系统或系统),其中X是一个紧致度量空间,T:X→X是一个连续映射.设d表示度量空间X的度量.



min{d(Tmxi,Tmxj):1≤i≠j≤n}≥ε.
这样的ε>0称为系统(X,T)的一个n初值敏感常数[2].

设(X,T)为动力系统,由文献[3],∀n≥2,令

Δn:{x1,…,xn}为一个S-集}.
1 预备知识
κ={F:+F}={F:F∩F′≠,



).
定义

定义1⊂,对取定的自然数n≥2,系统(X,T)称为-n-初值敏感的是指,存在ε>0,使得对任意非空开集U均存在n个互异的点x1,x2,…,xnU满足

这样的ε>0称为系统(X,T)的一个-n-初值敏感常数.
假设(X,T)是一个动力系统,⊂,定义
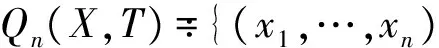
我们称X的子集w为x相对于的ω极限集.由定义可知yω(x,T)当且仅当N(x,U)对于y的任何邻域U成立.称点xX为一个-传递点,如果ω(x,T)=X.称xX为一个回复点,如果xω(x,T)[6].
易见,若x是动力系统(X,T)的-传递点,那么集合

是Xn的稠密子集;若T是开映射,是滤子,则Wn的每一个元素都是-回复的,此时Xn中所有-回复点所组成的集合也是稠密的.
定理1 设(X,T)是一个动力系统,T为开映射,是滤子并且是左平移不变的,-传递点集非空,n≥2是正整数.若(X,T)为n-初值敏感,那么.此外,若(X,T)为极小系统,且Qn(X,T)Δ(n)≠,那么(X,T)为-n-初值敏感的.


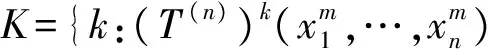


如果(X,T)为极小系统,假设Qn(X,T)Δ(n)≠,且(x1,x2,…,xn)Qn(X,T)Δ(n).因为点x1,x2,…,xn互不相同,故存在点xi的两两不交的闭邻域Ai(i=1,…,n).令δ=min{d(Ai,Aj):i≠j}.



且有

因此(X,T)是-n-初值敏感的.
引理1[5]设(X,T)为拓扑动力系统.族与系统(X,T)兼容当且仅当对于X中的任意非空闭集V,κ(V)是Fσ集.
下文将用到如下记号:
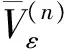
i≠j,使得d(xi,xj)≤ε};

C为一个集合}.
定理2 (X,T)为拓扑动力系统,如果是滤子对偶,且与系统(Xn,T(n))兼容.则对于
(1)存在ε>0,使得是Xn中的稠密集;
(2)存在ε>0,使得κ是Xn中的第一范畴集;
(3)(X,T)是-n-初值敏感的;
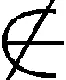
有(1)⟺(2)⟹(3)⟹(4).
证明(1)⟺(2):由Baire定理可知(1)等价(2).
κ()(x1,…,xn-1)=Cn(x1,…,xn-1).
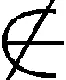
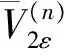


κ⊃κ([A1]δ×…×[An]δ)⊃
κ([A1]δ)×…×κ([An]δ),
则κ是Xn中的稠密集.如果是满族,则κ⊂,那么也是Xn中的稠密集.由定理2,动力系统(X,T)是-n-初值敏感的.
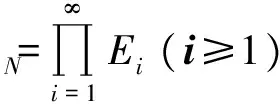

命题1 若是满族,则(∑N,σ)(N≥2)是-n-初值敏感的.
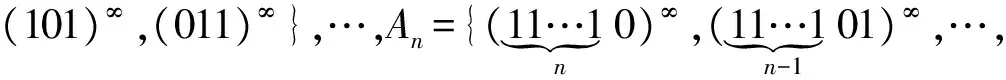
3 相对于集合K的初值敏感
定义2⊂,设(X,T)为拓扑动力系统,K为X的子集且满足Card(K)≥2.称系统(X,T)是相对于集合K为初值敏感的是指,对任意的(x1,…,xn)KnΔn,均有L(x1,…,xn)=X成立,即对点xi的任意邻域Ui及任意yX和y的邻域U,存在U满足:{k+:Tk()Ui,1≤i≤n}成立.这样的集合K称为是一个初值敏感集或-S-集.
对任意n≥2,令
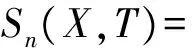
定义3[3]集合S⊆X称为是局部proximal集(或Q集)是指对任意的n≥2及任意点串(x1,…,xn)Sn,均有(x1,…,xn)Qn(X,T).
定义4⊂,集合S⊆X称为是局部proximal集(或-Q-集)是指对任意的n≥2及任意点串(x1,…,xn)Sn,均有(x1,…,xn)).
定理4 设(X,T)是一个动力系统,T为开映射,是滤子并且是左平移不变的,-传递点集非空,则任一S-集必为-Q-集.而且当(X,T)为极小系统时,任一Q-集必为-S-集.


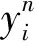
命题2 系统(X,T)的-传递点集是稠密的Gδ集,如果(X,T)是-n-初值敏感的(n≥2),那么.
证明设(X,T)是-n-初值敏感的.设点xTrans(X,T),Um为点x的开邻域且满足对任意的m,diam(Um)<1/m.于是由定义知存在ε>0使得对任意的自然数m,存在Um,满足:



[1] GUCKENHEIMER J.Sensitive dependence on initial conditions for one-dimensional maps[J].Comm Math Phys,1979,70:133-160.
[2] XIONG J.Chaos in topological transitive systems[J].Science in China:Ser A,2005,48(7):929-939.
[3] 张瑞丰.动力系统初值敏感性,序列熵及相关问题的研究[D].合肥:中国科学技术大学,2008.
[4] AKING E.Recurrence in topoligical dynamical systems,furstenberg families and ellis actions[M].New York:Plnum press,1997.
[5] XIONG Jincheng,LÜ Jie,TAN Feng.Furstenberg families and chaos[J].Science in China:Ser A,2007,50(9):1325-1333.
[6] SHAO S.Proximity and distality via Furstenberg families[J].Topology and its Applications,2006,153:2055-2072.
Keywords:-n-sensitivity;sensitivity set;transitive point
【责任编辑 庄晓琼】
THESENSITIVITYQUESTIONUNDERSOMERESTRAINEDCONDITIONS
ZENG Tiaoying, LÜ Jie*
(School of Mathematics, South China Normal University, Guangzhou 510631, China)
An important topic of dynamical complexity is the sensitivity.Under some conditions which include especial restrictions on orbit’s time set and visiting set,the sensitivity of topological dynamical system is investigated,and several properties concerning this sensitivity are obtained.
2010-04-27
国家自然科学基金项目(10771079);广州市教育局市属高校科技计划项目(08C016)
*通讯作者,ljie@scnu.edu.cn
1000-5463(2011)02-0038-05
O192
A

