一类各向异性Ginzburg-Landau超导模型的涡漩

寇艳蕾

(华南师范大学数学科学学院，广东广州 510631)

一类各向异性Ginzburg-Landau超导模型的涡漩

寇艳蕾

(华南师范大学数学科学学院，广东广州 510631)

当磁场hex充分接近第一临界磁场HC1时，证明了各向异性Ginzburg-Landau超导模型的整体极小元有有限个涡漩,并且说明这些涡旋的具体位置.

临界磁场; 涡漩; 各向异性; Ginzburg-Landau模型

对各向异性Ginzburg-Landau超导模型的研究缘于高温超导体的发现[1-3].高温超导体的一个重要特点是层状结构 (layered structure),它是由超导材料和非超导(或弱超导)材料呈现层状交替组成.在平行于每个分层的平面上，材料是各向同性的.但是，当比较平行于和垂直于材料的分层时，就会看到强烈的各向异性.

DU[4]提出各向异性的Ginzburg-Landau超导模型.将简化的自由能密度

推广到一般的自由能密度

这个表达式包括了各向同性和各向异性的Ginzburg-Landau超导模型.函数a(x)表示薄膜的厚度变量，而函数b=b(x)用来描述物体是否含有杂质：在理想超导体中(不含杂质)，b(x)=1；普通导体(含有杂质)中,b(x)<0.矩阵M(x)则用来表示空间的各向异性.

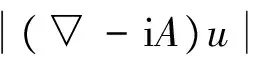
这时，能量泛函为

(1)

2≤ajk(x)ξjξk≤Λ2,∀ξ2.

目前，在超导理论上的研究已经有了大量的成果.下面简要回顾一下各类超导模型的研究历史和主要结果.

当A≠0，系数矩阵为

时，能量泛函为

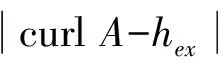
(2)

这里 ▽A=▽-iA，hex≠ 0.与简化模型相比，这个模型中的诱导磁场A≠0，说明这种模型考虑外磁场的影响.BETHUEL等[5]最早开始研究这种带磁场的完整的Ginzburg-Landau模型，得到与文献[6]类似的结论.CHAPMAN等[7]推导了3维Ginzburg-Landau泛函的2维极限形式.SERFATY[8]研究了这类模型的下临界磁场HC1的取值，以及下临界磁场HC1附近的局部极小元，即Euler-Lagrange方程的解.并讨论了这些解的涡漩的结构和性质.文献[9]研究了Euler-Lagrange方程解的渐近性态.

当A=A0，系数矩阵为

时，能量泛函为

DING等[11-13]详细研究了这种薄膜模型，得到下临界磁场和解的涡漩结构等结论.

当A≠0，系数矩阵为一般形式

时，能量泛函为

(3)

这是本文主要研究的各向异性的Ginzburg-Landau超导模型.

设(u,A)是J(u,A)在H1(Ω,C)×H1(Ω,2)上的极小元，则 (u,A)满足Euler-Lagrange方程

(4)

极小问题满足以下边界条件：

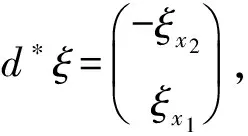
由于

(5)

这里aij=aij(x)(i,j=1,2).令方程的通解为φ(x,y)=φ1(x,y)+iφ2(x,y)=C,做自变量的变换

(6)

我们把下面的方程称为London方程

(7)

文献[14]研究了泛函(3)的局部极小元，证明了在集合

中存在泛函(3)的极小元，这里

并得到外加磁场hex的第一临界值HC1和极小元的渐近性质.

在文献[15]中，我们证明了下面的结论:

且对任意ε<ε0,有以下结论成立:

定理B只证明了磁场没有涡漩的情形.对于一般情形，即不管有没有涡漩并没有给出答案.与文献[15]相比，本文证明了定理A找到的局部极小元就是整体极小元，不管其是否有涡漩.此外，当外磁场在第一临界磁场HC1的附近时，还将证明整体极小元有有限个涡漩并指出这些涡漩的位置.

1 预备引理和主要结果

本文的主要结果是下面2个定理.

为了更好地说明第2个结论，首先定义涡漩.与文献[14]略有不同，这里定义的涡漩的半径较大.

由文献[16]的命题1可得下面的引理.

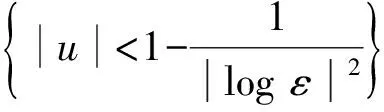
(8)

(9)

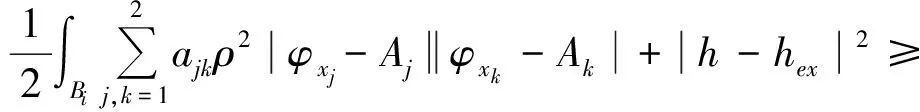
(10)

下面说明第2个结论.

(i)di≥ 0;

在这一节里,首先把泛函(3)分成两部分，然后估计泛函(3)的下界.

类似于文献[16]，可得到下面的引理.

(1)在Ω∪iIBi上，=1，并且和u/在∂Bi(iI)上有相同的拓扑度;

证明因为u=ρeiφ，那么

(11)

这里C是常数.注意到

ρ2(φxj-Aj)(φxk-Ak)=ρ2(φxjφxk-2φxjAk+AjAk)

(12)

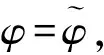
(13)

由于 (iu,ajkuxj)=ajkρ2φxj,从而得到

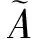
(14)

可得

(15)

从而有

这样

另外，由文献[15]的结论可知

(16)

引理3 对任意的p<2，存在α(p)>0使得

注意到

-curl(X-1d*h)+h=curl(iu,▽u)-

(17)

引理3的证明见文献[16]的引理II.2.

对能量泛函进行分割，并得到它的下界估计.注意到

(18)

并把系数矩阵记为

定义

(19)

取(1,hex(X-1d*ξ0))作为实验函数，则

J(u,A)≥

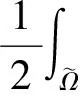
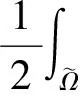
(20)

其中{(ai,di)}是引理1中定义的涡漩.

证明由引理1的式(10)可得

(21)

记u=ρeiφ，用d*h取代*dh，则由式(4)的第2个式子可得

-d*h=(X·▽Au,iu)=ρ2X(▽φ-A),

[(▽ρ+iρ(▽φ-A))eiφ]T·X·[(▽ρ-iρ(▽φ-

A))e-iφ]≥2+ρ2(▽φ-A)T·X·(▽φ-A)≥

(d*h)TX-1(d*h).

(22)

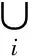
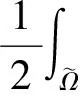
(23)

令h=hexξ0+f，则上式中的最后2项变为

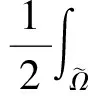
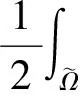
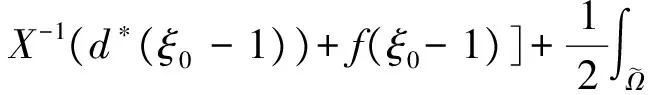
代回可得

J(u,A)≥

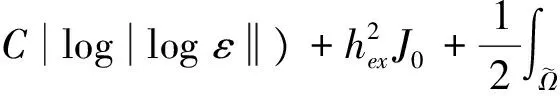
(24)

由式(18)可知

-(d*h)TX-1(d*h)+h=-(d*f)TX-1(d*f)+

f-hex[(d*ξ0)TX-1(d*h0)+ξ0]=

-(d*f)TX-1(d*f)+f.

对上式进行分部积分得到

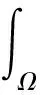
得到

J(u,A)≥

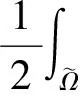
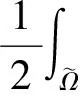
引理证毕.

2 定理2的证明

证明取(1,hex(X-1d*h0))作为实验函数，而(u,A)是式(3)的极小元，则有

引理证毕.

由文献[13]的引理3.1，有如下引理.

(25)

引理7 定理2的(i)成立,即di≥ 0.

证明记

(26)

(27)

由于ξ0在Ω上是负的，p(x)在Ω上是正的，则

(2)如果di<0，那么

应用引理1及式(20)，可得

(28)

从而

这样对足够小的正数ε，有D-=0.又因为D-一定是非负的，所以di≥ 0.

证明由文献[16]可知

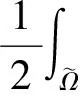
(29)

从而

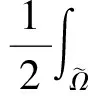
(30)

结合上面2个不等式可得

上式说明D有一致的上界.

这样就得到了定理2的证明.

3 定理1的证明

设(u,A)是泛函J在Ω上的极小元，则

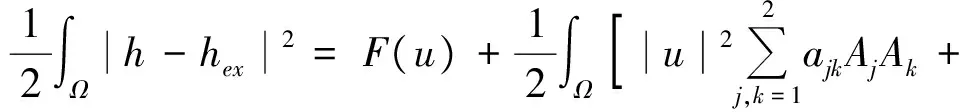
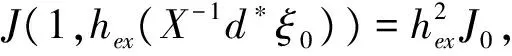
这样

在Ω/∪iIB(ai,ρ)上，不妨设=r.由于H3(Ω)≤Chex，则

在Ω/∪iIB(ai,ρ)上，记u=reiφ可得

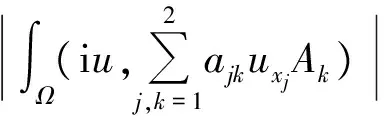
定理1证毕.

[1] CHAPMAN S J,DU Q,GUNZBURGER M D.A Ginzburg-Landau type model of superconducting/normal junctions including josephson junctions[J].Euro J Appl Math,1995,6(2):97-114.

[2] IYE Y.How anisotropic are the cuprate highTCsuperconductors?[J].Comments Cond Mat Phys,1992,16:89-111.

[3] HAO Z,CLEM J.Comment on “From isotropic to anisotropic superconductors:a scaling approach ” and authors’ reply[J].Phys Rev Lett,1993,71:301-302.

[4] DU Q.Dynamics in model of coarsening,coagulation,condensation and quantization[M]. Singapore:World Scientific Press,2007:63-140.

[5] BETHUEL F,RIVIERE T.Vortices for a variational problem related to superconductivity[J].Ann Inst H Poincare Anal Non Lineaire,1995,12(3):243-303.

[6] BETHUEL F,BREZIS H,HELEIN F.Ginzburg-Landau vortices[M].Boston:Birkhauser,1994.

[7] CHAPMAN S J,DU Q,GUNZBURGER M D.A model for variable thichness superconduction thin films[J].Z Angew Math Phys,1996,47(3):410-431.

[8] SERFATY S.Local minimizer for the Ginzburg-Landau energy near critical magnetic field:Part I[J].Commun Contemp Math,1999(1):213-254.

[9] SERFATY S.Local minimizer for the Ginzburg-Landau energy near critical magnetic field:Part II[J].Commun Contemp Math,1999(1):295-333.

[10] DU Q,GUNZBURGER M D.A model for superconducting thin films having variable thickness[J].Physica D,1993,69:215-231.

[11] DING S,DU Q.The global minimizers and vortex solutions to a Ginzburg-Landau model of superconducting thin films[J].Comm Pure Appl Anal,2002,1(3):327-340.

[12] DING S,DU Q.Critical magnetic field and asymptotic behavior of superconducting thin films[J].SIAM J Math Anal,2002,34(1):239-256.

[13] DING S,DU Q.On Ginzburg-Landau vortices of superconducting thin films[J].Acta Mathematica Sinica:English Series,2006,22(2):469-476.

[14] KOU Y L,DING S.Derivation of lower critical magnetic field for anisotropic Ginzburg-Landau model in superconductivity[J].Acta Mathematica Sinica:English Series,2011,27(5):953-982.

[15] 寇艳蕾，丁时进.各向异性Ginzburg-Landau超导模型整体极小元[J].华南师范大学学报:自然科学版,2008(4):7-16.

KOU Yanlei,DING Shijin.The global minimizers of anisotropic Ginzburg-Landau model in superconductivity[J].Journal of South China Normal University:Natural Science Edition,2008(4):7-16.

[16] SANDIER E,SERFATY S.On the energy of type-II superconductors in the mixed phase[J].Rev Math Phys,2000(12):1219-1257.

Keywords： critical magnetic field; vortices; anisotropic; Ginzburg-Landau model

【责任编辑 庄晓琼】

VORTICESOFANANISOTROPICGINZBURG-LANDAUMODELINSUPERCONDUCTIVITY

KOU Yanlei

(School of Mathematics,South China Normal University,Guangzhou 510631,China)

The global minimizers and the vortex structure of an anisotropic superconducting model are discussed.It is proved that for fieldshexclose enough to the lower critical magnetic fieldHC1,the global minimizer of the Ginzburg-Landau functional has a bounded number of vortices independently from the Ginzburg-Landau parameter.The locations of these vortices are also given.

2010-09-07

*通讯作者，kouyanlei@tom.com

1000-5463(2011)02-0013-07

O175.25

A