基于推进学习策略的对传神经网络
林励莉,王 涛,林 拉
(华南师范大学计算机学院,广东广州 510631)
基于推进学习策略的对传神经网络
林励莉,王 涛,林 拉*
(华南师范大学计算机学院,广东广州 510631)
结合Adaboost算法的加权投票机制,提高对传神经网络CPN(Counterpropagation Networks)的学习效率,提出新型快速分类算法(简称为ACPN).实验证明,新算法的学习最小误差比传统CPN算法下降了96%,训练时间同比下降44%,网络训练阶段误差下降趋势明显稳定.
对传神经网络; 分类算法; 推进学习; 预测波动性
对传神经网络CPN是集成了自组织映射结构Kohonen和外星结构Grossberg的一种混合神经网络算法.简单的拓扑结构和有效的学习算法,使CPN在模式识别和预测模型建模应用领域中与同时期的其他神经网络相比(如Rumelhart & McClelland提出的BP网),在运行效率上有更大的优势.
预测模型的目标是挖掘输入样本与目标数据的映射规律,利用映射规律分析新数据,给出正确率较高的预测结果.因此,一个预测模型的预测结果正确率直接体现模型的实用价值.目前提高CPN预测精度的优化主要在于样本预处理和算法过程改进.NIELSEN[1]曾提供一种思路,每次竞争允许多个神经元同时获胜,并指派获胜系数ρ给每个获胜神经元以区分获胜等级,训练样本和神经元的距离Dxk与ρ成反比,所有获胜系数之和为1.但随后在证明上面这种思路的预测精度不及传统CPN算法[2].WU等[3]则专注于样本优化问题的研究,提出应区分训练集和测试集,避免实验结果过度拟合(overfit),并在CPN中成功运用Kennard-Stone算法和D-Optiaml思想实现训练集和测试集的合理分割,实验结果Kennard-Stone效果比D-Optiaml更优.文献[4]-[6]利用Kohonen网络特性,将N组样本按压缩比例σ,输入m*m的Kohonen神经网络,其中m、σ满足关系m*m≈σ*N.保留训练中被激活的神经元及其权值作为预测模型建模的输入,实现任意σ比例的学习样本压缩.从而降低噪声数据在训练时对预测模型的影响,有利于改善预测模型的预测精度.
此外,在算法过程优化方面,CHANG[7]结合CPN和Fuzzy模糊逻辑控制思想提出对传模糊神经网络CFNN,该算法建模阶段采用CPN算法,预测模型应用阶段对最大类间距Δ加入模糊自动放大调整,扩大了CFNN模型在降雨径流量估算上的实用性,尤其对未知因素的处理.而LIU等[8]利用自适应共振理论ART,从输入样本的自相似度自动生成Kohonen层神经元,并根据最新的训练数据动态调整,解决Kohonen层神经元数量和输入权重的初始化问题.宋晓华等[9]通过改进CPN算法的初始权重设置规则,克服了对输入向量限制过于严格的不足.上述文献大部分是由于特定领域数据处理的需要,而对CPN进行扩充.本文关注在时间权衡下如何提高CPN预测模型的预测精度,结合Adaboost算法的加权投票机制,提出了一种新型快速分类算法(ACPN).
1 传统CPN算法
CPN应用有2种类型:一类是纯粹挖掘样本之间的潜在关系,则不需要提供测试样本YM,即结果完全由输入样本特征决定;另一类是发现输入样本与期望结果之间的关系,则需要提供YM在预测模型建模时指导学习,本文讨论后者.


图1 传统CPN网络结构

(1)

(2)
有教师指导学习阶段:Kohonen层获胜神经元kg确定后,Grossberg层将这一结果映射到输出层,即将kg与Grossberg输入权向量vg作为第k组目标输出(见式(3)).式(4)是Grossberg层输入权向量vg的调整公式,由等式可见调整是以期望输出yk作为参考,体现了期望值的指导作用.经过足够多的调整后,输入权向量vg将接近期望值yk.由文献[10]可知,学习率β取值范围取[0.01,0.5],在初始阶段可取较大值加快学习速度,后期逐步下调学习率至0.01或更少,以提高训练精度.

(3)

(4)
NIELSEN[2]证明在足够多的神经元经过有教师训练后,能找到Kohonen层聚类结果wg=φ(xk)与目标向量yk之间的线性映射关系yk≈φ(wg),使每个输入向量x对应唯一一个输出向量y,若实际输出向量与目标输出向量一致,则训练效果最佳,当然要注意是否有过度拟合问题.
对传神经网络CPN的指导学习方式是模仿人类的反复识记法,将样本反复地输入CPN网络进行训练,使预测模型能识别训练样本与目标数据的关系,学习效率不高,识别能力有限.由式(2)、(4)可以看到调整学习率可以加快学习速度,若单纯通过加大学习率加快学习速度,容易“欲速不达”(如学习过程中漏掉潜在的弱映射关系).本文第2节结合Adaboost的投票机制为CPN提供一套新的学习方案.
2 改进算法(ACPN)
NIELSEN[2]的CPN算法给后人一个启示,基础神经网络算法的合理组合应用,也许会产生意想不到的效果,本节描述的改进算法(ACPN)是在CPN上集成Adaboost特点的混合神经网络.新算法的改进体现在2个方面:算法执行流程的调整和新型快速学习策略.
2.1算法执行流程调整
目前CPN的优化方案集中在样本预处理上,大部分保留了传统的Kohonen训练机制.传统CPN算法每轮训练是相对独立的,上一次训练的情况无法传递给下一轮,导致训练工作不断重复,预测精度也十分受限.为了打破这种局限,ACPN将预测模型的训练分为若干个弱预测模型同时进行,最终将所有弱预测模型整合为一个强预测模型.
2.2快速学习策略
一个好的学习策略是决定算法应用价值的关键因素.传统CPN网络采用的迭代学习方式,学习效率低,不利于CPN网络在高维或大训练样本中的应用.ACPN利用Adaboost强弱均衡的投票机制[11-12],在学习阶段添加2个学习变量:样本错误率uw和预测模型正确率cw.
训练样本错误率uw是记录每个样本在当前的弱预测模型训练中的表现,随着训练次数的增多,识别出错率越高的样本uw值将越大,表示该样本的识别难度大,而成功识别的样本则相反.进入下一个弱预测模型训练时,训练重点将放在难识别的样本上,从而缩短学习训练时间.
预测模型正确率cw是模型训练输出与预期输出的匹配数与训练样本数的比例,反映预测模型的预测精度.最终强预测模型的整合运用输出带权求和的方式,使预测精度高的弱预测模型有较大的影响力[13],算法具体执行流程见2.3节.
2.3ACPN算法
ACPN重点是改善传统CPN学习策略、加快学习速度和提高CPN建模的预测能力,为了避免噪声数据对模型训练的影响,样本预处理阶段采用Kennard-Stone设计,算法执行步骤具体描述如下:

(2)样本预处理:采用Kennard-Stone划分样本训练集和测试集,预处理过程如下:


end while


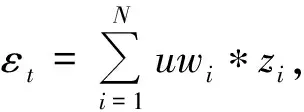

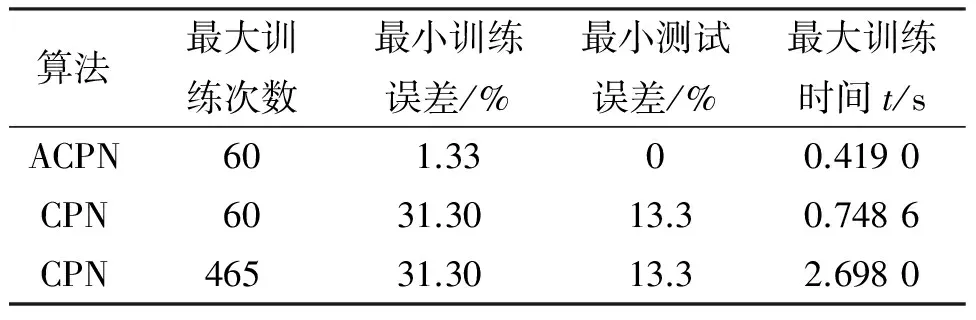
(4)若t (6)验证预测模型:验证过程与测试过程类似,这里不再重复描述. 本节通过在兰花类型预测上的应用,展示ACPN算法在学习时间和预测精度上的优势,实验所有数据均来源于UCI Machine Learning Repository数据库( http:∥archive.ics.uci.edu/ml/). 兰花预测模型是解决兰花类型的识别问题,所使用的兰花特征数据集由现代统计学与现代演化论的奠基者FISHER R A创建,样本属性4个分为3类,每类50个样本,无噪声数据.后期被大量模式识别研究文献所引用,并成为检测分类模型分类能力的一个基准. 关于训练集和测试集:为了保证实验结果的可比性,2个算法均使用相同的训练集、测试集. 关于竞争层神经元的选择:由于ACPN的竞争阶段和传统CPN一致,因此相同神经元数对2个网络的影响是一样的.MAREN等[14]建议神经元个数取值区间[x+1,y*(x+1)],其中x是输入样本的维数,y是输出结果的维数,本实验折中均取10个. 关于测试样本的选择:由于数据集结构层次清晰,本次实验省略样本的优化处理,测试样本(共30个)由每类数据随机选出1/5的样本组成. 表1通过比较2种网络建模的训练误差和测试误差,可见改进算法ACPN的预测效果远比CPN要好.同时,传统CPN算法的预测精度还是有限的,即使增多训练次数,无法达到ACPN的效果.从而验证了在改进算法下的预测模型的预测能力. 表1 ACPN算法和传统CPN算法的对比Table 1 Contrast between ACPN and CPN 图2 传统CPN兰花预测模型 图3 ACPN兰花预测模型 对传统CPN算法、CPN-S[9]算法、添加Kenstone样本优化的CPN算法以及本文改进算法ACPN进行对比,结果表明,前3个算法随着训练次数的增多,训练误差有所下降,但预测误差无明显变化,改进算法预测精度明显比其他算法要高. 预测模型的目标是从样本数据中发现规律,利用数据中的规律分析新数据,给出正确率较高的预测结果,因此一个预测模型的预测结果正确率直接体现模型的实用价值;同时,运行时间也是评价一个预测模型的重要因素. 表2 CPN、CPN-S、CPN-K和ACPN算法比较Table 2 The comparison among CPN、CPN-S、CPN-K and ACPN 注:训练出错率=训练样本预测出错数/训练样本总数,测试出错率=测试样本预测出错数/测试样本总数,运行时间=训练时间+测试时间. 本文提出了基于Adaboost算法的加权投票机制的新型对向传播神经网络ACPN,该算法在考虑时间的权衡下,通过改善学习策略提高CPN网络学习效率.实验结果证明,新算法预测误差下降趋势的波动性明显比传统CPN算法小,保证预测精度的稳定性,提高预测模型的实用价值. [1] NIELSEN R H.Applications of counterpropagation networks[J].Neural Networks,1988,1(2):131-139. [2] NIELSEN R H.Neurocomputing[M].USA:Addison Wesley Publishing Company,1990:147-155. [3] WU W,WALCZAK B,MASSART D L,et al.Artificial neural networks in classification of NIR spectral data:Design of the training set[J].Chemometrics and Intelligent Laboratory Systems,1996,33(1):35-46. [4] ZUPAN J,NOVI M,RUISNCHEZ I.Kohonen and counterpropagation artificial neural networks in analytical chemistry[J].Chemometrics and Intelligent Laboratory Systems,1997,38(1):1-23. [5] ZUPAN J,GASTEIGER J.Neural networks in chemistry and drug design[M].New York:Weinheim,1999:44-46. [6] KANDU R K,ZUPAN J,MAJCEN N.Separation of data on the training and test set for modelling:a case study for modelling of five colour properties of a white pigment[J].Chemometrics and Intelligent Laboratory Systems,2003,65(2):221-229. [7] CHANG F J,CHEN Y C.A counterpropagation fuzzy-neural network modeling approach to real time streamflow prediction[J].Journal of Hydrology,2001,245:153-164. [8] LIU T C,LI R K.A new ART-counterpropagation neural network for solving a forecasting problem[J].Expert Systems with Applications,2005,28(1):21-27. [9] 宋晓华,李彦斌,韩金山,等.对传神经网络算法的改进及其应用[J].中南大学学报:自然科学版,2008,39(5):1059-1063. SONG Xiaohua,LI Yanbin,HAN Jinshan,et al.An improved counter propagation networks and its application[J].Journal of Central South University:Science and Technology,2008,39(5):1059-1063. [10] VRACKO M,MILLS D,BASAK C S.Structure-mutagenicity modelling using counter propagation neural networks[J].Environmental Toxicology and Pharmacology,2004,16:25-36. [11] FREUND Y,SCHAPIRE R E.A short introduction to boosting[J].Joural of Japanese Society for Artificial Intelligence,1999,14(5):771-780. [12] 贾慧星,章毓晋.基于动态权重裁剪的快速Adaboost训练算法[J].计算机学报,2009,32(2):336-341. JIA Huixing,ZHANG Yujin.Fast adaboost training algorithm by dynamic weight trimming[J].Chinese Journal of Computers,2009,32(2):336-341. [13] FREUND Y,SCHAPIRE E R.A decision-theoretic generalization of on-line learning and an application to boosting[J].Journal of Computer and System Sciences,1997,55:119-139. [14] MAREN A J,HARSTON C T,PAP R M.Handbook of neural computing applications[M].San Diego:Academic Press,1990:240-243. Keywords: Counterpropagation Neural Network; classified algorithm;adaptive improved learning; forecasting volatility 【责任编辑 庄晓琼】 IMPROVEDCOUNTERPROPAGATIONNETWORKSWITHADAPTIVELEARNINGSTRATEGY LIN Lili, WANG Tao, LIN La* (School of Computer, South China Normal University, Guangzhou 510631, China) A novel adaptive boosting theory-Counterpropagation Neural Network(ACPN) for solving forecasting problems is presented.The boosting concept is integrated into the CPN learning algorithm for learning effectively. Compared with traditional CPN,the minimal training error and learning time in ACPN network fell about 96% and 44%,respectively.Furthermore,the curve of trainning error in ACPN presents downtrend basically and has less fluctuation. 2010-09-13 *通讯作者,linla@scnu.edu.cn 1000-5463(2011)02-0060-05 TP 39 A
3 实验结果




4 结论


