线性流形上D反对称矩阵的加权最小二乘解

张华珍

(湘西民族职业技术学院，湖南 吉首 416000)

线性流形上D反对称矩阵的加权最小二乘解

张华珍

(湘西民族职业技术学院，湖南 吉首 416000)

通过矩阵的奇异值分解得到了线性流形上D反对称矩阵在加权范数下的最小二乘解，同时导出了解集合中与给定矩阵的加权最佳逼近解的表达式。

加权；D反对称矩阵；最小二乘

对于矩阵方程在加权范数下的最小二乘解的研究到目前为止已取得了一系列的成果[1-3]。下面，笔者在此基础上运用矩阵的奇异值分解研究线性流形上D反对称矩阵的加权最小二乘解。

1 问题的提出

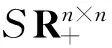
定义1[4]给定D=diag(d1,d2,…，dn)∈Rn×n,其中dr>0，r=1,2,…,n。A∈Rn×n,若D2A∈ASRn×n,则称A为D反对称矩阵，D反对称矩阵的全体记为D-2ASRn×n，显然：

D-2ASRn×n={A|A=D-2B,B∈ASRn×n}

记D2SRn×n={A|A=D2B,B∈SRn×n}，令：

S={A∈D-2ASRn×n|AX0-B0=min,X0,B0∈Rn×m}

(1)

由文献[4]知，S是非空的线性流形。下面笔者考虑如下问题：

问题Ⅰ 给定X,B∈Rn×k，求A∈S使得：

‖AX-B‖W=min

(2)

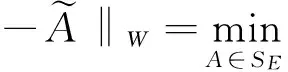
(3)

其中，SE是问题Ⅰ的解集合。

2 问题Ⅰ的解

引理1设D2X的奇异值分解为:

其中,U=(U1,U2)∈ORn×n；U1∈Rn×t；V=(V1,V2)∈ORm×m；V1∈Rm×t；Σ=diag(σ1,σ2,…,σt)；σi>0，i=1,2,…,t。则式(1)中集合S有下面的形式：

(4)

其中:

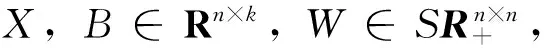
(6)

其中，P=(P1,P2)∈ORn×n；Q=(Q1,Q2)∈ORk×k;P1∈Rn×r；Q1∈Rk×r；∑1=diag(α1,α2,…,αr)；α1≥…≥αr>0；r=rank(W-1X)。

记:

(7)

则问题Ⅰ的解集合为：

(8)

其中:

(9)

证明因为A∈S,所以由引理1中式(4)可知:

(10)

则:

由式(11)可知，‖AX-B‖W=min等价于：

(12)

由引理2及式(12)中第1式可知:

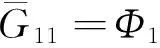
(13)

由式(12)中第2式可知:

(14)

将式(13)和式(14)代入式(10)即可得到式(8)，(9)。

3 问题Ⅱ的解

引理3[4]∀A∈Rn×n，则存在惟一的A1∈D-2ASRn×n，A2∈D2SRn×n使得:

A=A1+A2〈A1,A2〉=0

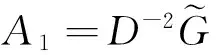
定理2符号与定理1相同，由定理1可知SE是一个闭凸集，因此问题Ⅱ存在最佳逼近解：

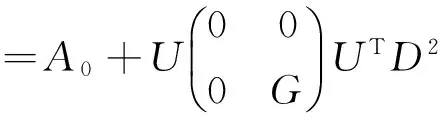
(15)

这里G如式(9)所示，其中:

(16)

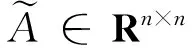
(18)

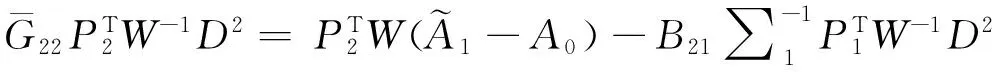
[1]周立平. 几类线性矩阵方程的加权最小二乘解及其最佳逼近问题[D].长沙：湖南大学，2007:1-48.

[2] 刘莉，张凯院.关于一类矩阵方程的加权最小二乘解[J].昆明理工大学学报(理工版)，2006,31(3)：121-124.

[3] 孟国艳，赵青杉，赵俊华.反对称正交反对称矩阵反问题的加权最小二乘解[J].太原师范学院学报(自然科学版)，2008,7(1)：13-17.

[4] 张忠志，周富照，胡锡炎.D反对称矩阵反问题的最小二乘解[J].中南工业大学学报.2001,32(5)：545-548.

[5] 谢冬秀，张磊.一类反对称矩阵反问题的最小二乘解[J].工程数学学报，1993,10(4)：25-74.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.04.002

O241.6

A

1673-1409(2011)04-0005-03