超低速永磁同步电动机及其在坦克炮控系统中的应用

2011-11-20 08:35李立宇李长兵朱志昆

微特电机 2011年12期

李立宇，李长兵，朱志昆，袁东

(装甲兵工程学院，北京100072)

0 引言

炮控系统是坦克火力控制主线末端的执行系统，具有驱动和稳定坦克火炮/炮塔的功能，是充分发挥火控系统性能，实现“先敌开火、首发命中”的重要保证［1］。不管是电液式还是全电式炮控系统，由于驱动电机的旋转速度通常都很高，故系统中都需要由多级齿轮组成的减速机械传动装置。而齿轮传动装置中不可避免地存在传动间隙及齿轮弹性形变，这一非线性环节对炮控系统的稳定性、低速性能和稳定精度(通常认为系统稳定精度仅能达到系统传递误差的1/2左右)会产生重大影响，这就制约了系统性能的进一步提高。

本文提出的座圈电机无间隙传动方案，水平向采用大直径、多极、超低速永磁同步电动机，并设计成与现有炮塔座圈相似的结构，电机定子与车体联接固定，电机转子直接与炮塔固定，转子转动直接驱动炮塔旋转。无间隙传动方案消除了炮控系统中机械传动间隙带来的技术瓶颈问题，为炮控系统性能的进一步提升，探索了一种新的技术解决方案。

1 电机参数选型

根据某型坦克座圈结构，可确定座圈电机的定子外径和转子内径尺寸;根据该坦克炮控系统最大调炮速度和最低瞄准速度等性能指标及斜坡调炮要求，可折算出电机转速为0.003～5.83 r/min，额定功率为1.8 kW，额定转矩为2 950 N·m。根据上述基本参数要求，考虑到推力轴承的最大游隙量，经计算和仿真分析，方案设计中所确定的电机参数如表1所示。

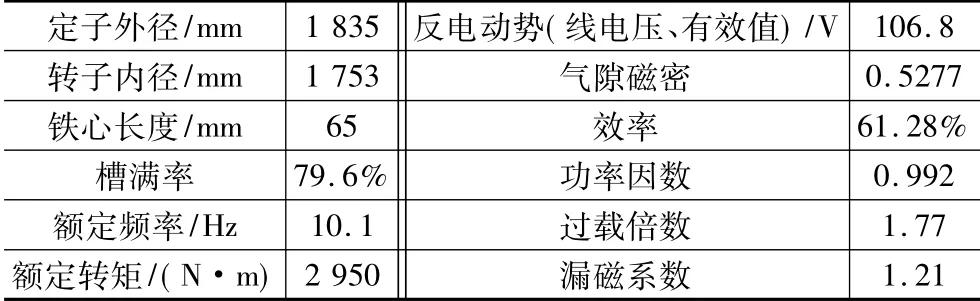
表1 电机性能参数

2 电机电磁设计

2.1 极槽配合的选取

不同的极槽配合对电机转矩波动的影响也不同［2］。本文对208极234槽和198极216槽两种极槽配合的永磁同步电动机进行对比分析后选取较优的极槽配合方案。

用Ansoft软件对两台电机进行建模，分析其一个单元电机的空载气隙磁场波形如图1和图2所示。

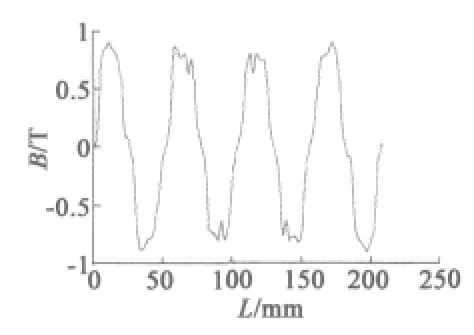
图1 208极234槽永磁电动机气隙磁密波形

图2 198极216槽永磁电动机气隙磁密波形

用傅里叶分析软件对以上两台电机的气隙磁密波形进行谐波分析所得谐波幅值占基波幅值的百分比，如图3和图4所示。

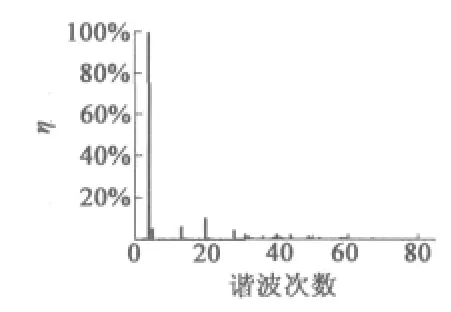
图3 208极234槽永磁电动机气隙磁密分析

图4 198极216槽永磁电动机气隙磁密分析

计算两台电机气隙磁场的谐波正弦性畸变率，208极234槽永磁电动机的谐波正弦性畸变率为0.150 5，198极216槽永磁电动机谐波正弦性畸变率0.155 5。可见，208极234槽永磁电动机的气隙磁密波形正弦性要优于198极216槽永磁电动机。

图5、图6为通过Ansoft软件计算得出的两种极槽配合电机的齿槽转矩波形。

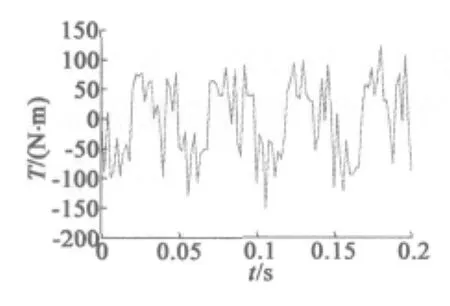
图5 208极234槽电机齿槽转矩波形

图6 198极216槽电机齿槽转矩波形

由图5、图6可以看出，198极216槽永磁同步电动机齿槽转矩的波动范围是从－210～280 N·m，而208极234槽永磁同步电动机齿槽转矩的波动范围是从－150～125 N·m，明显低于前者的齿槽转矩波动。

综合分析以上两种极槽配合的方案，最终选择208极234槽的极槽配合。

2.2 漏磁系数的计算

整数槽电机的漏磁系数可以通过磁场有限元的方法准确求出。但对于分数槽电机尤其是真分数槽电机，通过上述方法求出的漏磁系数误差较大。真分数槽电机的特点是齿数和槽数的大小相近，这样就在出现了极间和齿顶两种漏磁，如图7所示。

图7 径向方向漏磁路分布示意图

齿顶漏磁的出现增加了电机的漏磁系数，也给电机漏磁系数的准确计算带来了难度。对于多极少槽的极槽配合可以利用Ansoft求出电机的静态磁场，再分别求出电机的极间漏磁、齿顶漏磁和电机的总磁通，代入漏磁计算公式求出电机的漏磁系数为1.21。也可以利用Ansoft瞬态场计算出电机的空载反电动势，再通过公式E0=4.44fKdpNΦδ0KΦ，反推出电机的漏磁系数［3］。图8为选定永磁同步电动机的空载反电势波形，通过傅里叶分析可得电机空载反电动势的基波幅值为120.58 V，再反推电机的漏磁系数为1.20。由于以上分析均采用二维磁场，没有考虑电机的端部漏磁的影响，所以在选取电机的漏磁系数时要加上端部漏磁系数。最终选取电机的漏磁系数为1.21。

图8 超低速永磁同步电动机空载反电势波形

2.3 单边磁拉力的影响

电机由于加工和安装的误差，定、转子可能不同心，使气隙磁场中的磁密不相等产生单边磁拉力。单边磁拉力作用在定、转铁心子上，使铁心发生变形。所以有必要对电机在受到单边磁拉力的情况下，定、转子铁心发生的变形和受到的应力大小进行分析。

径向电机单边磁拉力的计算公式［4］:

式中:β为经验系数，同步电动机和直流电动机可取0.5;D为转子铁心外径;led为转子铁心长度;Bδ为气隙磁密幅值;e0为初始偏心，计算时可取0.1δ;δ为单边平均气隙长度;μ0为真空磁导率。

通过计算得到电机所受的单边磁拉力为6 137 N。假设单边磁拉力集中作用在定、转子相距最近的一条线上，用ANSYS分析这种极限情况时的变形和受力情况如表2所示。

表2 转子变形量和应力的大小

由以上计算结果可知，转子厚度为15 mm时的变形量仅为0.007 5 mm。远小于电机气隙单边厚度4 mm的10%，满足设计要求。

3 电机结构设计

大直径、多极、超低速座圈电机是将永磁电动机设计成与炮塔座圈相似，炮塔直接与电动机转子固定，转子中心轴挖空，转子转动直接驱动炮塔旋转，定子与坦克车体固定不动，连接成一体，定、转子之间同轴度由大直径的推力轴承保证。方案设计中的大直径推力轴承借用了某型坦克上的原车座圈。安装时，将电动机的空心转子通过座圈上安装孔固定在座圈的旋转面上，定子通过座圈下安装孔固定在车体上，定、转子轴向延伸在座圈的下方形成相互作用空间，组成一体后即成为完整的座圈电机。电机与轴承配合的总装配图如图9所示。

图9 电机与轴承配合总装配图

由于电机的直径大，且转子为空心结构，故不便安装电机速度和位置传感器。解决方案如下:利用原座圈上的齿条，在转子联结板上安装一个弹性齿轮与齿条啮合，编码器与齿轮轴相连如图10所示。弹性齿轮选取18个齿与座圈齿条相配合，当炮塔旋转时编码器也同时旋转，从而获取速度信息。在电机定子A相绕组轴线处，安装3个互差120°电角度的霍尔元件，以确定电机起动时转子的位置。编码器与霍尔元件的安装如图11所示。

图10 齿轮与齿条配合示意图

图11 编码器与霍尔元件的安装示意图

4 系统控制方案

永磁同步电动机的电磁转矩主要取决于定子直轴(d轴)和交轴(q轴)的电流分量。由于永磁同步电动机转子磁链不变，所以可采用转子磁链定向方式来控制［5］。为了简化系统，可把合成电流矢量控制在q轴而无d轴分量，即id=0，iq=i。假设永磁同步电动机各种参数不会随温度变化，并忽略涡流、磁滞损耗，且转子无阻尼绕组，其在d－q坐标系中的定子电压方程和转矩方程可以表示如下:

式中:，ud、uq为定子电压矢量u在d、q轴上的分量，Lq为交轴电感;ω为转子角频率;p为微分因子;rs为定子相电阻;p为电机极对数;Ψ为转子磁钢在定子上的耦合磁链［6］。

从式(1)～式(3)可以看出，只要准确检测出转子位置(d轴)，可通过控制逆变器使得三相定子合成电流位于q轴，则永磁同步电动机的电磁转矩Td仅与定子电流幅值成正比，即通过控制定子电流的幅值，就可以很好的实现对电磁转矩的控制［7］。

图12为按转子磁链定向控制(FOC)的永磁同步电动机矢量控制原理图。

图12 永磁同步电动机FOC控制原理框图

根据转速和转矩的关系，由参考转速和电机实际转速通过速度PID调节输出得到定子电流的参考输入。先用Clarke变换将定子相电流ia和ib转换到定子两相静止坐标系中，再用Park变换转换到d－q旋转坐标系中。d－q旋转坐标系中的电流信号与参考输入量isqref和isdref比较(其中isdref=0)，并通过两个PI调节器获得理想的控制量。该控制量再通过Park逆变换作为SVPWM逆变器的输入，从而得到控制定子绕组的实际电流值。速度环得到定子电流的参考值，电流环产生实际控制量，从而构成了一个完整的FOC双闭环控制系统［8－9］。

图12中矢量控制所用到的坐标变换定义如下:

Clarke变换: