直线永磁无刷直流电动机端部力的分析

黄文美，薛雅洁，宋桂英

(河北工业大学，天津300130)

将式(4)和式(5)代入式(3)中，简化后得:

0 引 言

直线永磁无刷直流电动机具有推力大、定位精度高及易于控制等优点，越来越多的应用于工业自动化，有着广泛的应用前景。直线电动机是一种将电能直接转换成直线运动机械能而不需要任何中间转换机构的装置;传统的有刷电动机中电刷和换向器组成的机械换向装置，其间的滑动接触严重的影响了电机的精度和可靠性，缩短电机寿命，需要经常维护，所产生的火花会引起无线电干扰。无刷直流电动机采用功率电子开关(如GTR、MOSFET、IGBT)和位置传感器代替电刷和换向器组成机械换向器，既保留了直流电动机优良的运行性能，又具有交流电动机结构简单、维护方便和运行可靠等特点［1－2］。

直线永磁电机也有其不足之处。与旋转电机相比，直线电动机最大的不同之处在于它的动子铁心是长直的、开断的，所以，动子铁心端部磁场会发生畸变，这就影响到行波磁场的完整性，进而对电机推力造成波动影响，影响电机的性能，这就是端部效应。而直线电动机的特殊结构使得端部效应是不可避免的，在实际应用中应设法削弱端部力，使电机系统的失稳性降低。文献［3］采用斜极法来削弱端部力，这种方法不易于电机加工，实际应用意义不大;文献［4］中采用遗传模拟退火算法削弱推力波动，得到了合理的电机参数，但是这种方法对于电机结构参数具有约束性，只是针对部分型号电机，不具有普遍性;文献［5］采用线圈补偿的方法来削弱端部力，这会增加电机的重量和成本，也不利于电机控制。

本文提出了从优化动子结构方面来削弱端部力的方法，并建立了仿真模型，验证了该优化方法的可行性。这种方法易操作，成本低，适合大部分直线电动机。

1 直线永磁无刷直流电动机动子长度的优化

1.1 端部力数学解析模型

直线永磁无刷直流电动机模型的磁场分布如图1所示，动子模型忽略了齿槽结构。可以看出动子铁心两端端部磁场发生畸变，当给线圈绕组通入三相正弦交流电时，动子铁心在这个磁场作用下做直线运动，但是由于直线电动机铁心端部发生开断，使得两个端部的线圈电感和动子铁心中部的线圈电感不同，造成三相绕组的磁通不等，端部磁导和永磁体作用形成了两个切向的推力F1、F2，这两个力之和即为永磁直线无刷直流电动机的端部力Fend:

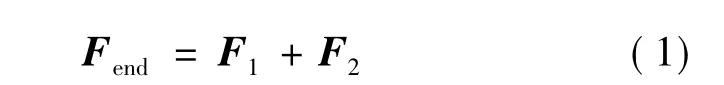
各力的分布示意图如图2所示。

图2 永磁直线无刷直流电动机模型

根据麦克斯韦张量法，推算出电机水平推力表达式:

式中:μ0为磁导率;ω 为动子纵向厚度，Bx、By分别为电机磁场水平和垂直方向分量。S为包围动子铁心的曲线，nx、ny为法向量分量。

由式(2)可计算出式(1)的端部力。可得:

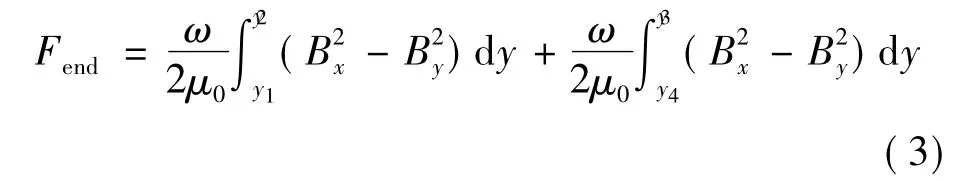
根据气隙磁场的推导，得:

式中:Br为永磁体的剩磁;τ为极距;τs为永磁体宽度;hs为动子铁心的高度;Hs为动子铁心到永磁体表面的高度。令:

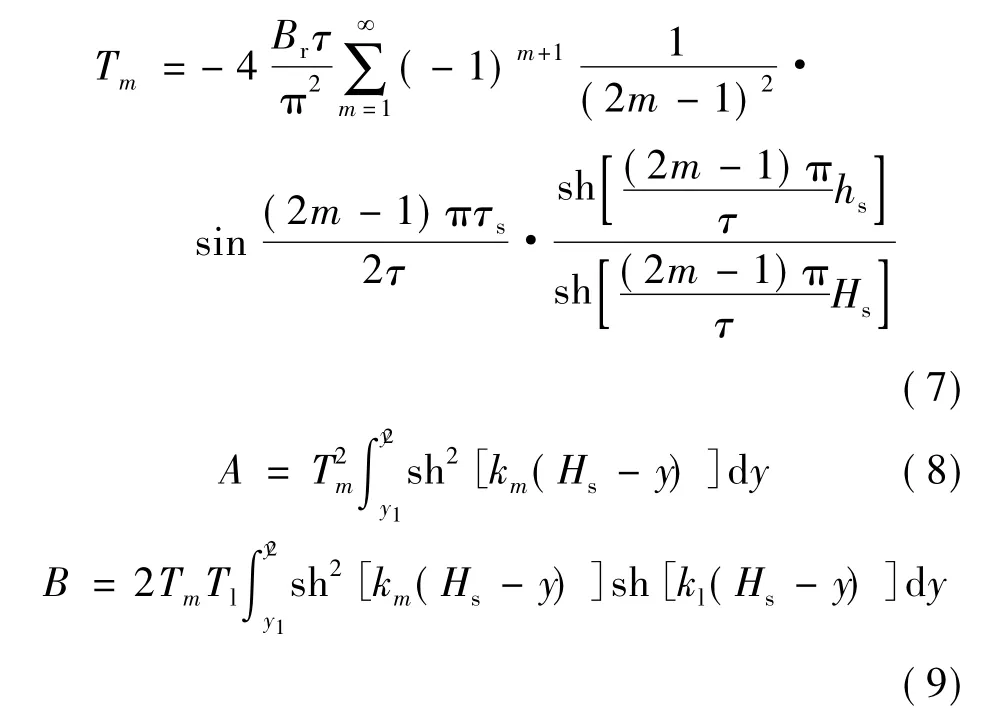
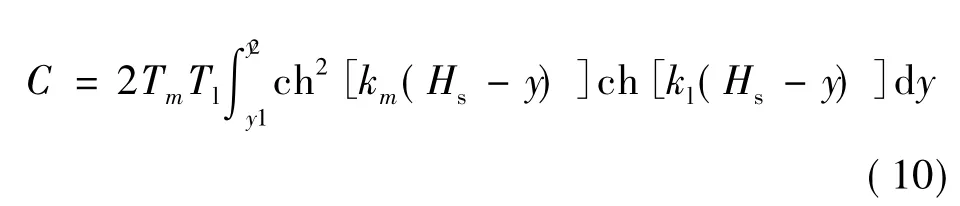
将式(4)和式(5)代入式(3)中，简化后得:

式中:x0为动子铁心中心位移坐标;L为铁心长度。

从式(11)中分解出各项系数，分别为:1+

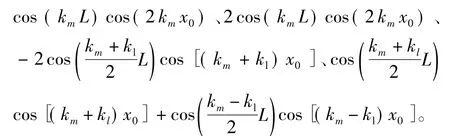
从以上各项系数中可以看出，当L一定时，这些系数都是关于x0的周期函数，且周期为极距τ;当动子在0～τ范围运动时，这些系数是随着L周期性变化，且周期为 2τ;当 L=(0.5+n)τ，n=1，2，3，…时，cos(kmL)等于零。

通过以上分析可以得出，端部力的波动是和动子位置相关的周期性波动函数，且周期为极距τ;当动子在0～τ内运动时，端部力的大小和动子长度有关，周期为2τ，若仅考虑幅值变化，则周期为τ;当L=(0.5+n)τ，n=1，2，3，…时，端部力有最小值。

1.2 有限元法实验验证

永磁直线无刷直流电动机参数如表1所示。

表1 电机仿真模型参数

建立如图1所示的忽略齿槽结构的Ansoft仿真模型，以动子长度L为变量，利用有限元法进行验证，结果如下:

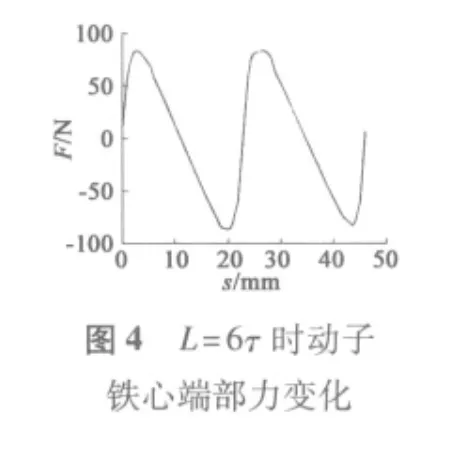
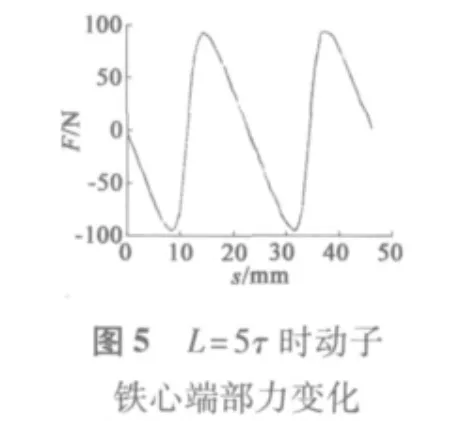
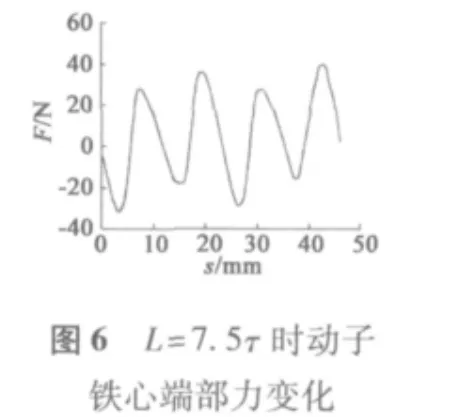
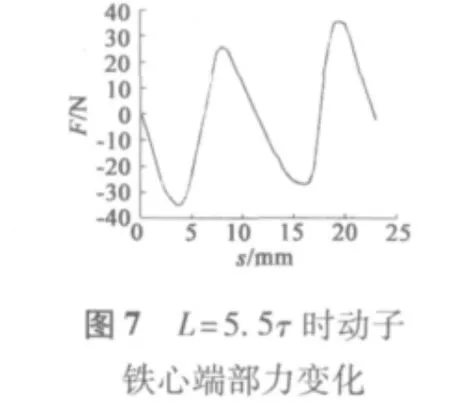
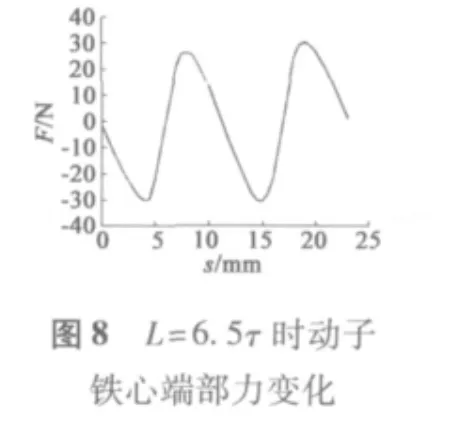
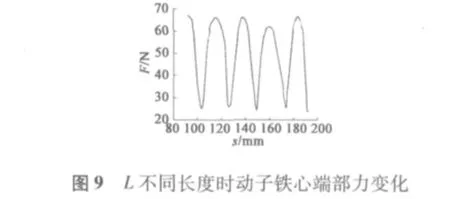
1.3 实验结论分析

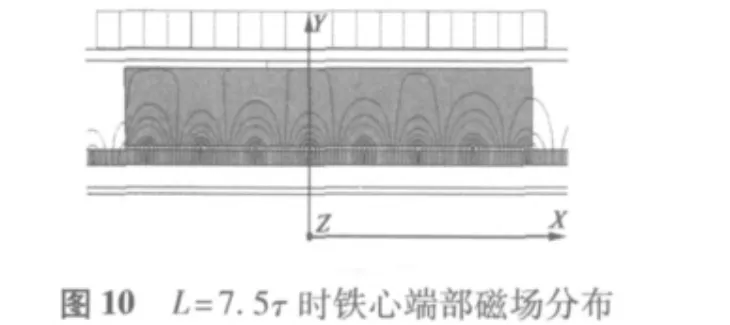
通过对比不同动子长度下的端部力大小，从图3～图6中可以看出，当动子长度在0～2τ范围内运动时，端部力大小呈周期性变化，且周期为τ;端部力变化在L=4τ和L=6τ时基本相同，最大值约为89 N，与L=5τ时幅值基本相同，相位相差180°;当L=7.5τ时相较于L=4τ、L=5τ时端部力波动范围较小，最大值约为40 N;从图9中可以看出，端部力是随着铁心长度周期性变化的，且在L=(k+0.5)τ时端部力有最小值。图10、图11中显示出L=7.5τ和L=4τ时磁场分布，可以看出，在忽略齿槽结构模型中铁心端部磁场分布在L=7.5τ时优于L=4τ时动子铁心端部磁场分布。图6～图8对比了L=5.5τ、L=6.5τ、L=7.5τ时端部力的变化，可以看出L=6.5τ时端部力最大值较小，约为30.7 N。

2 永磁直线无刷直流电动机动子形状的优化

2.1 建立优化模型

由于端部效应是在铁心端部的气隙磁阻发生了急剧变化而导致的，因此可以把动子端部设计为过渡结构来削弱端部力。

2.1.1 圆弧过渡结构

图12为铁心端部为圆弧的较平滑结构的Ansoft仿真模型。

图12 L=7.5τ时圆弧结构的铁心端部磁场分布

2.1.2 梯形过渡结构

图13为铁心端部为梯形结构的Ansoft仿真模型。

图13 L=7.5τ时梯形结构的铁心端部磁场分布

2.2 实验结论分析

图14、图15分别给出了铁心端部采用圆弧过渡结构和梯形结构，当动子铁心在0～τ范围运动时端部力的变化。

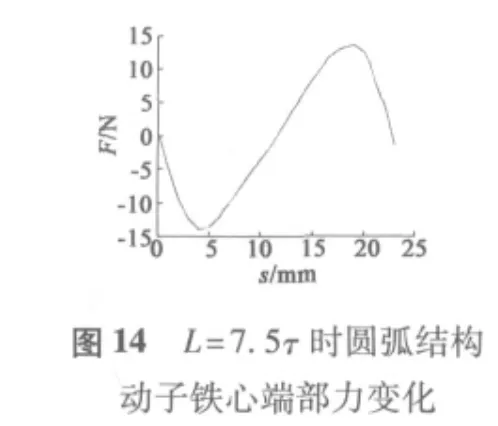
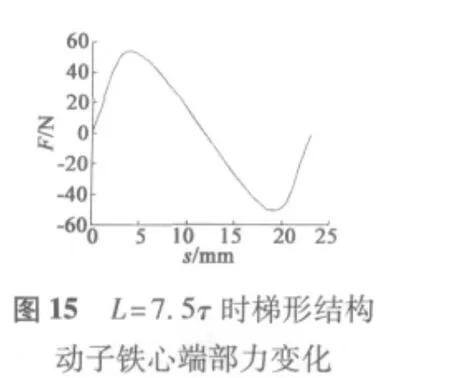
可以看出，相较于图6，采用圆弧过渡结构的动子铁心端部力较小，其最大值由40.026 N下降到14.147 N，下降了约64%;而采用梯形过渡结构的动子铁心端部力最大值约为53.8 N，相较于图6则较大，所以实验排除了梯形过渡结构的动子结构，选用圆弧过渡结构的动子结构。

3 结 语

本文针对永磁无刷直流电动机的端部效应问题，结合对端部力的理论分析以及运用有限元法仿真，通过对不同动子长度时端部力的比较，证明了通过改变动子长度来削弱端部力是可行的;端部力是关于动子长度的周期函数，当动子长度为(k+0.5)τ时，端部力有最小值;其次，采用Ansoft软件计算了动子端部圆弧结构和动子梯形结构时端部力的大小，验证了动子端部采用圆弧结构时端部力相对减弱。这在实际应用中削弱端部力对推力的波动影响有很大帮助。实验确定动子长度为149.5 cm，端部为圆弧过渡结构，有限元法计算端部力最大值约为8.7 N。

［1］ 夏加宽.高精度永磁直线电机端部效应推力波动及补偿策略研究［D］.沈阳:沈阳工业大学，2006.

［2］ 李皞东.电火花机床用永磁直线电机的端部效应及其控制的研究［D］.沈阳:沈阳工业大学，2002.

［3］ Lee S－H，Park S－B，Kwon S－O.Characteristic analysis of the slotless axial－flux type brushless DC motors using image method［J］.IEEE Transactions on Magnetics，2006，42(4):1327 －1330.

［4］ 陈宇，卢琴芬，叶云岳.长定子同步直线电动机的设计及其优化［J］.电工技术学报，2003，18(2):18 －21，40.

［5］ 李治源，关晓存.感应线圈炮电枢与驱动线圈间纵向动态边端效应的影响［J］.微电机，2010(6):13－15.

［6］ 张颖.永磁同步直线电机磁阻力分析及控制策略研究［D］.武汉:华中科技大学，2008.

［7］ Lee J Y，Kim S I，Hong J P.Optimal Design of Superconducting Motor to Improve Power Density Using 3D EMCN and Response Surface Methodology［J］.IEEE Transactions on Applied Superconductivity，2006，16(2):1819 －1822.

［8］ Faiz J，Jafari H.Accurate Modeling of single－ sided linear induction motor considers end effect and equivalent thickness［J］.IEEE Trans.on Magnetics，2000，36(5):3785 －3790.