极数对永磁无刷直流电动机性能影响的研究
上官璇峰,张 涛
(河南理工大学,河南焦作454003)
0 引 言
一般永磁无刷直流电动机主要由电动机本体、位置传感器和电子开关线路三部分组成。永磁无刷直流电动机具有旋转的磁场和固定的电枢,电子开关线路可直接与电枢绕组相连,位置传感器和电子开关线路则代替了有刷直流电动机的机械换向器[1]。
通常情况下,电动机本体定子多为三相结构,绕组为分布式或集中式,且多为Y接法。当无刷直流电动机定子为三相对称绕组时,由于气隙磁场为梯形波,只能采用星形接法。若采用三角形接法,由于三次谐波的存在会增加附加损耗,其输出转矩也较小。电机的电枢绕组放在定子上,转子励磁采用永磁材料,瓦片型永磁体直接粘贴在转子铁心上。
在永磁无刷直流电动机中,起重要作用的是永磁体的性能,在选用稀土永磁材料的情况下,极对数的多少直接影响着电机性能。选择极数时应综合考虑电机的运行性能和经济指标,设计电动机时,有时要选取几种极数进行方案比较,才能确定合适的极数。在电机主要尺寸确定,选择极对数时,应综合考虑运行性能和经济指标,参照直流电动机极对数选择方法进行分析比较。
1 性能研究
电机模型的主要参数如下:额定功率PN=600 W,额定电压 UN=200 V,额定转速 nN=1 200 r/min,极弧系数 α =0.75,定子内径为 75 mm,定子外径为120 mm,转子直径为74 mm,气隙长度δ=0.5 mm,铁心长度La=65 mm,槽数Q=24,绕组方式为双层绕组,绕组形式及电子开关形式采用两相导通星形三相六状态,极数为4/8极。
1.1 在不同充磁方式下的四极电机研究
瓦片形磁极有两种充磁方式:径向充磁和平行充磁。径向充磁时的充磁方向都为径向,而平行充磁时的磁化方向与永磁体的中心线平行。在极数为4时,用这两种充磁方式时磁场分布如图1所示。

图1 径向和平行充磁时磁场分布
4极平行充磁方式和4极径向充磁方式比较可以发现,图1(b)中有一部分磁力线直接进入电动机以外的空气包中,所以在平行充磁时,电动机的漏磁比较大。
根据有限元法[2]可知:k是一个n阶的系数矩阵,p是一个n行的矩阵,第k'个节点为第一类边界条件上的节点,其磁位已知为Azk'0,得方程:
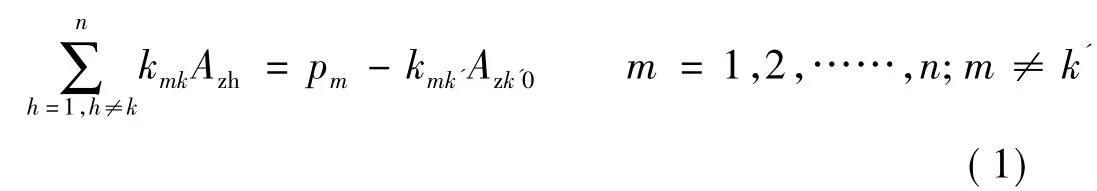
式中:kmh、kmk'分别是n阶矩阵中第m行第h列和和m行第k'列的值;pm是n行矩阵第m行所对应的值。
求解上式可得到求解区域内所有节点的磁位,再根据式:

得到相应场量。
使用Magnet软件,在电机模型中做一个半径为37.25 mm的圆,该路径上各节点磁位已知。若气隙剖分足够细,在圆周上各选取1 001个等角度的点,得出相对应的气隙磁通密度的值,则可得径向充磁和平行充磁的气隙磁通密度曲线,如图2所示。

图2 径向和平行充磁的气隙磁密
把所得的气隙磁密进行傅里叶变换,可得到相应的频域图,如图3所示。
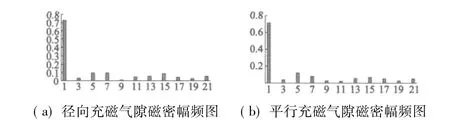
图3 径向和平行充磁气隙磁密幅频图
使电机旋转起主要作用的是基波,从上图可以看到,径向充磁的基波所占比值较大,其所产生的高次谐波,相对平行充磁的电机来说,对电机的转矩波动影响也较小。
当电机转子旋转时,永磁磁极产生的磁场是旋转的,而定子绕组是静止不动的,因此定子绕组和气隙磁场所交链的磁链随时间变化,在相绕组中感应出旋转电动势,则每相绕组的感应电动势幅值:

式中:Φ为每极磁通量;p为极对数;N为每相绕组串联匝数;α为极弧系数。
E的大小不仅决定电动机是运行于增磁状态还是去磁状态,而且对电动机的动、稳态性能均有很大的影响。合理的设计E可降低定子电流,提高电动机效率,降低电动机的温升。设计实践表明,所有设计比较成功的电动机,其E与额定电压的比值均在一定的合理范围内。
在上述参数的前提下,永磁体采用径向充磁和平行充磁,极数为4极,每槽导线60匝,电枢不通电的情况下,转子旋转半周。在定子绕组中产生反电动势,可得到如图4曲线。
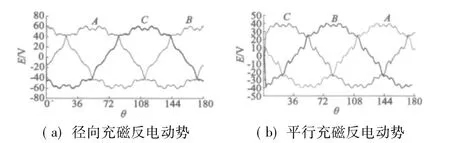
图4 4极径向和平行反电动势图
研究表明,换相引起的转矩脉动主要决定于绕组反电动势,也就是电动机的转速与电枢稳态电流无关。对于两相导通三相六状态矩形波永磁无刷直流电动机,当转矩很低或堵转时E=0,转矩脉动ΔT=50%;当转速很高时,转矩脉动ΔT=-50%;当转速满足 U=4E 时,ΔT=0[3]。
忽略磁路饱和,径向充磁时的气隙磁密表达式[4]:

平行充磁时的气隙磁密表达式:
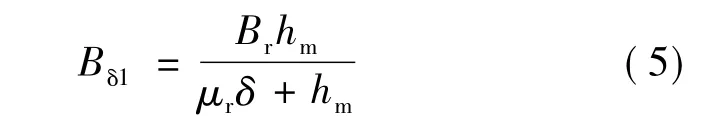
则气隙磁通:

再由式(3)可求得反电动势E。
式(4)~式(6)中,hm=35 mm,Da=74 mm,α'=0.767,τp=58.9 mm,则径向充磁和平行充磁的反电动势分别为E1=46.1 V和E2=40.68 V。
可以发现,径向充磁时,额定电压U=200 V,相反电动势波形为顶部不小于120°的梯形波,径向充磁时相反电动势有效值E1=46.1 V,即U≈4E,所以在径向充磁时换相引起的转矩脉动最小。然而在平行充磁时,相反电动势的有效值E2=40.68 V,差不多U≈5E。
给径向充磁和平行充磁的4极电机分别加4.77 N·m的负载,仿真时间分别是60 ms和100 ms,所得瞬态电磁力矩波形如图5所示。
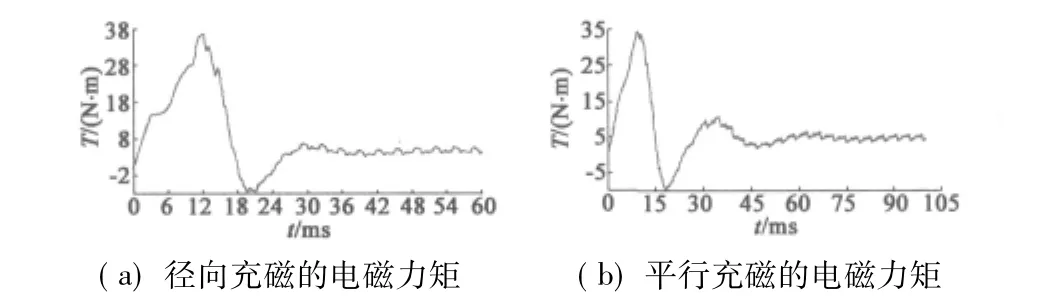
图5 径向和平行充磁时电磁力矩图
从图5比较可以发现,4极径向充磁的电机在40 ms时已趋于稳定,而4极平行充磁的电机在80 ms才开始趋于稳定,并且波动较大。
1.2 4极和8极电机的对比研究
使用软件Ansoft 12,把上述主要参数输入RMxprt中的永磁无刷直流电动机模块中,在计算时,RMxprt模块采用等效电路方法计算电机模型,所以计算周期非常短暂。
通过改变极对数为4极和8极,分别在Solution Data中得到的详细数据,仅列出一部分如表1所示。

表1 4极和8极电机的各项损耗及效率
理论上,在同样转速下,定子绕组电流的交变频率将随极数的增加而增加,因而齿的铁损耗随极数的增加而增大,而定子轭铁损耗则增加很少,因为铁轭的重量随极数增加而下降;当极数增加时,绕组端部明显减小,从而定子绕组中的铜耗随极数的增加而降低。在本方案中,极数增加时,铜耗降低比铁耗增加大,故总损耗减小,8极的效率比4极高。
电动机的运行效率直接影响电能的有效利用,也影响电动机本身的温升。它是衡量电动机质量的重要指标之一。因此,各类电动机在额定运行时的效率在有关技术条件中都有具体规定,有时还规定效率的容差,在设计电动机时要保证达到规定的效率。由于目前应用的直流无刷电动机的功率均较小,其能耗指标并不十分突出,在保证其他性能指标的前提下,有时允许牺牲点效率。
假定直流母线电压U是一个常数,电机工作于两相导通星形三相六状态工作方式。直流母线电流等于导通相绕组的电流值。在每个导通时间内,电枢相电流:
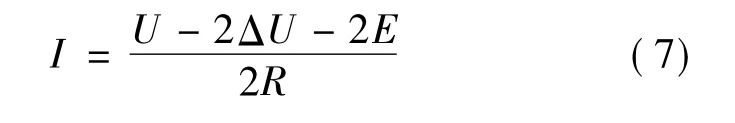
式中:U为电源电压;ΔU为开关器件饱和压降;E为每相电枢绕组感应电动势;I为每相绕组电流;R为每相绕组电阻。
使用软件Ansoft 12进行二维有限元仿真,4极电机在在瞬态运行时,求解时间为60 ms,步长为0.3 ms,得到A相的电流曲线如图6(a)所示。而8极电机在瞬态运行时,求解时间为20 ms,步长为0.1 ms,所得电流曲线如图6(b)所示。
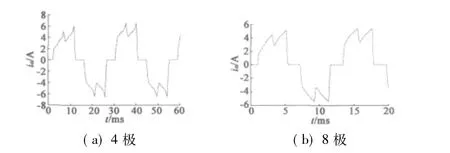
图6 4、8极电机的A相电流
从图上可以看到,所得曲线并不是理想的矩形波,而是在通电过程中有很大波动的凹陷,这主要原因是因为绕组开始通电时,电感影响了电流的大小。比较4极和8极电机电流可以看到,8极没有4极电机电流受到的影响大,这是因为磁极增多后,定子绕组电感相应减少,从而对电流的影响就小。
基于有限元法,利用麦克斯韦张量法可以方便地计算电磁转矩。首先在气隙内取一包围转子的闭合路径,根据磁场有限元计算的结果,得到气隙磁密的切向分量Bθ和Br,则力的切向分量密度fθ和径向力密度fr分别为:

根据该闭合路径上的切向力密度,就可得到所产生的转矩:

式中:D为闭合路径的直径。取D=74.5 mm,4极电机在瞬态运行时,求解时间为60 ms,步长为0.3 ms,得到电磁力矩曲线如图7(a)所示。然而8极电机在瞬态运行时,求解时间为20 ms,步长为0.1 ms,所得电磁力矩曲线如图7(b)所示。

图7 4、8极电机瞬态运行时的电磁转矩曲线
忽略工艺影响,永磁无刷直流电动机的转矩波动主要包括齿槽引起的齿槽转矩、电流换向引起的转矩波动、电磁因素引起的转矩波动、电枢反应引起的转矩波动。通过比较我们发现,4极和8极在峰值大小上没有差别,但是在8极电机的波动大,这主要是因为增加极对数后,在同样的转速下,电子器件的换相频率增加,从而增大了换向对转矩波动的影响。但8极电机在较短时间就能达到稳定的电磁转矩。
2 结 语
从上述分析可以看到,电机的各项性能分析是一个复杂的整体,改变任何一个参数,都会引起许多参数相应发生变化。虽然不能在相同条件下研究一个变量,但是它们之间还是有一定的关系可寻,根据需要合理选取极对数,对电机性能改善和减少生产成本,都是有很大好处的,并且也对合理利用我国的稀土永磁材料有着积极的意义。
[1] 刘刚,王志强,房建成.永磁无刷直流电机控制技术与应用[M].北京:机械工业出版社,2008:31-34.
[2] 王秀和.永磁电机[M].北京:中国电力出版社,2007:55-176.
[3] 魏静微.小功率永磁电机原理、设计与应用[M].北京:机械工业出版社,2009:152-176.
[4] 王秀和,李岩,吴延中,等.径向充磁永磁电机工作点的确定[J].电工电能新技术,1998(3):44 -46.
[5] 赵博,张洪亮.Ansoft12在工程电磁场中的应用[M].北京:中国水利水电出版社,2010.

