快速傅里叶变换的并行化研究

赵晓雷，王 敏

(渭南师范学院数学与信息科学学院，陕西渭南714000)

快速傅里叶变换的并行化研究

赵晓雷，王 敏

(渭南师范学院数学与信息科学学院，陕西渭南714000)

研究了傅里叶变换及其实现形式快速傅里叶变换(FFT)，并给出了图像处理中FFT并行化算法，通过并行化模拟可以得出数据量愈大愈适合并行计算，当处理节点达到一定数量时它们的并行效果已不明显.

快速傅里叶变换;图像处理;并行化

0 引言

离散傅里叶变换(Discrete Fourier Transform，DFT)在计算机学科的图像处理领域有着广泛的应用，由cooley和Tukey［1］(1965)所研究出的计算离散傅氏变换的快速傅里叶变换(Fast Fourier Transformation，FFT)，将计算量从O(n2)下降到了Ο(nlog2n)，从而使FFT在诸多领域内得到了广泛的应用.随着数字图像的广泛应用，人们对图像处理提出了更高的要求，如何提高运算的速度得到了大家的关注，同时高性能集群计算机具有较高的性价比及其强大的运算能力得到了人们的重视，如何在PC并行集群计算机上提高离散傅里叶变换速度是研究热点.

1 傅里叶函数变换

1.1 傅里叶变换

假定f(m，n)是一个包含m和n两个变量的函数，则该函数的二维傅里叶变换定义形式如下：

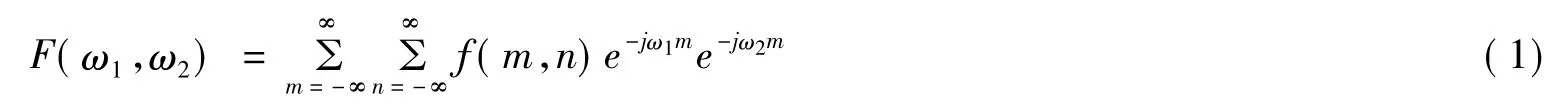
式 (1)中，ω1和ω2为频域变量，其单位为弧度 /采样单元.通常称函数F(ω1，ω2)为f(m，n)的频域表示，F(ω1，ω2)是复变函数，其中变量ω1和ω2的周期为2π，由于这种周期性，在图像显示时，两个变量的取值大小为：-π≤ω1，ω2≤π.

傅里叶反变换［2］定义如下：

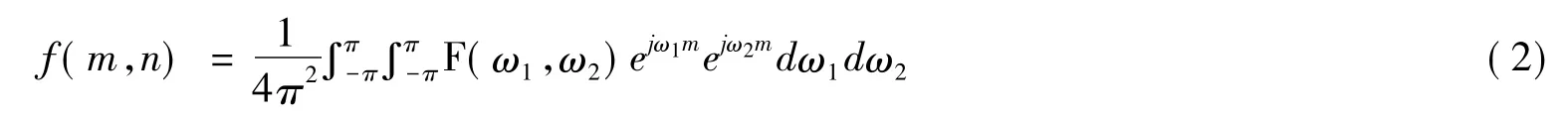
1.2 离散傅里叶变换及快速傅里叶变换

计算机在处理傅里叶变换时采用离散傅里叶变换(DFT)，采用离散傅里叶变换基于如下原因：

(1)由于离散傅里叶变换是建立在离散的数据基础之上的，适合计算机参与运算处理.

(2)可以采用一种快速傅里叶变换(FFT)来实现离散傅里叶变换.

快速傅里叶变换［3］的设计思想是：首先将原函数通过傅里叶变换将其分解为奇数项和偶数项，将分解得到的奇数项和偶数项不停地进行相加减运算，最终得到运算的结果，实际上该算法的实现过程就是将较为复杂的乘法运算转换为简单的加减法运算，通过一定量的加法运算来代替乘法运算，从而降低运算的复杂度，提高运算的速度.

对于的N=2m的DFT的计算，通过计算两个N/2点的DFT来得到N个的DFT.

设离散函数f(m，n)在区域0≤m≤M-1，0≤n≤N-1内非零，则二维的M×NFFT和M×N逆FFT关系如下：

从而可以得出，F(p，q)是f(m，n)的DFT系数.

其中 p=0，1，…，M-1;q=0，1 ，…，N-1;m=0，1，…，M-1;n=0，1，…，N-1.

离散傅里叶变换(DFT)由于含有大量的加法和乘法从而其运算量级在N2，快速傅里叶变换(FFT)是将DFT进行分解为加法，从而使运算量降低到Nlog2N.FFT算法在图像上的实现过程如下：

读入图像矩阵后，对其转置矩阵［4］按照以行进行一维FFT变换，将经过变换的转置矩阵再进行一次转置变换得到一个新的矩阵，后对新矩阵做一维的FFT变换，最终得到的矩阵就为图像的二维FFT变换矩阵.

1.3 集群计算机下基于BSP模型下的并行FFT

为了适应图像并行处理的实时性要求，在进行图像并行处理时需要一个并行计算机系统，从而引入了集群计算机系统架构［5］，该系统是以网络工作站NOW(net works of workstation)形式的集群计算机，在该系统上配以负载平衡、动态任务分配机制、消息传递机制等技术，通过高速网络连接构成单一资源镜的系统软件，是COW(cluster of workstation)的一种集群形式，具有COW所具有的属性，其性质如下图所示：

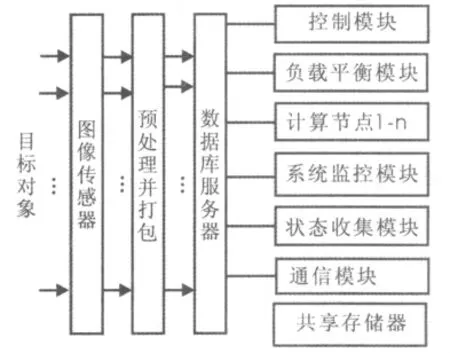
图1 实时集群计算机处理系统结构图

2 图像FFT处理并行化设计

图像的快速傅里叶变换的并行算法设计如下：

首先假定图像的大小为DateSize，参与并行运算的处理机个数为TasKNum，在整个并行处理系统中，首先主控节点按照如下步骤运行：

(1)首先接受用户的输入，便可以得到参与运算的图像的大小为DateSize，同时可以从外部输入得到参与并行计算的从节点数TaskNum，从而得到一个大小为DateSize1的数;

(2)主控节点产生TaskNum个进程，通过集群计算机中负载平衡系统分配到各个从节点上进行计算;

(4)主节点等待接收从节点传来的结果数据;

(5)在主节点上对接收的数据排序，并进行IFFT反变换，结束程序.

从节点()

(1)接收主节点传来的DataSize1、TaskNum和Id参数;

(2)依据算法的思想，可以得到为每个节点分配的数据位为：Ptask_Node=DataSize1/TaskNum;

(3)在各个节点上进行FFT计算，并得到计算的结果;

(4)将从节点中得到的计算结果通过进程控制发送到主控节点;

(5)从节点结束运算.

2018年11月5日，以“新时代，共享未来”为主题的首届中国国际进口博览会在上海隆重开幕。展会吸引了全球172个国家/地区和国际组织的3600多家企业参会，展览总面积达30万m2，进博会既是世界期待、万商云集的经贸盛宴，也是中国向世界学习、与国际接轨的发展良机。SEW作为世界领先的传动领域供应商之一，以其经典的“SEW红”精彩亮相2018进博会，充满浓重的工业色彩和强烈视觉冲击的展位引起众多观众驻足。

为了尽可能快的提高处理速度，在进行图像分块时尽可能进行整数分块，假设有n个处理机，在进行模块分配时，模块的大小应为2n，这样既能将图像进行充分的分配模块，又能保证图像完全进行分配，不至于有多余的部分没有分配，从而加长处理的总时间量，这些操作通过系统的进程进行分配管理.

3 实验结果分析

加速比

加速比［6］的定义：

上式中p为并行运算中参与运算的处理机的数目，Tp为在个处理机上进行并行运算及相互间通信所耗费的时间，Ts为单机完成处理所需要的时间，研究并行算法的目的是：尽可能多的提高并行系统的加速比.通常在实际中引起加速比变化的原因如下：

(1)在算法的设计中，并行度不够完全或负载平衡分配任务不够合理;

(2)并行处理机相互间通信所在的时间比重过大;

(3)由于处理的任务量不够大而导致的并行度过小.

效率

并行效率：并行效率指的是在并行处理系统中所产生的加速比和该系统参与运算的处理机数目之比，并行效率的定义如下：

显然，O ＜Ep≤1，当Ep=1时，达到完全加速比.

为了验证该算法的有效性和可行性，对FFT变化和反变换在模拟并行环境中进行运算，表1是对图像circuit.tif进行FFT变换及其反变换，得到的测试结果.

实验中以256×256、512×512和1024×1024三个不同大小像素的图像，分别对其进行并行化模拟运算，假设试验中处理机数依次为 1，2，4，8.

从表中的加速比和效率数据可以看出，伴随着节点数的增加，它们的加速比有不断增大的趋势，但其效率伴随着节点数的增多也有增大的趋向，当处理机个数达到某个固定值4时，图像的并行效率达到最大值，随后随着处理机数的增加而其并行效率在降低，缘由在于当处理机个数不断增加时，它们相互之间的通行量会随着处理机个数增加而剧烈增大，从而使相互间的并行效率降低.从理论上可知，并行效率是伴随着加速比的增加而增大的，但从实际的试验数据中可以看出加速比和效率并不是随着处理机数的增加而无限增大的，当处理机个数达到某个固定值时，并行的效率并不能再提高，而是随着节点数增多时并行效率在降低，并行处理的意义已不再明显.从实验中的数据可以看出，对于不同规模的数据，当节点数趋于一个定值时，它们的并行处理效率达到最大;通过对效率分析，发现当数据量愈大采用并行处理时的加速比和效率有明显增大.

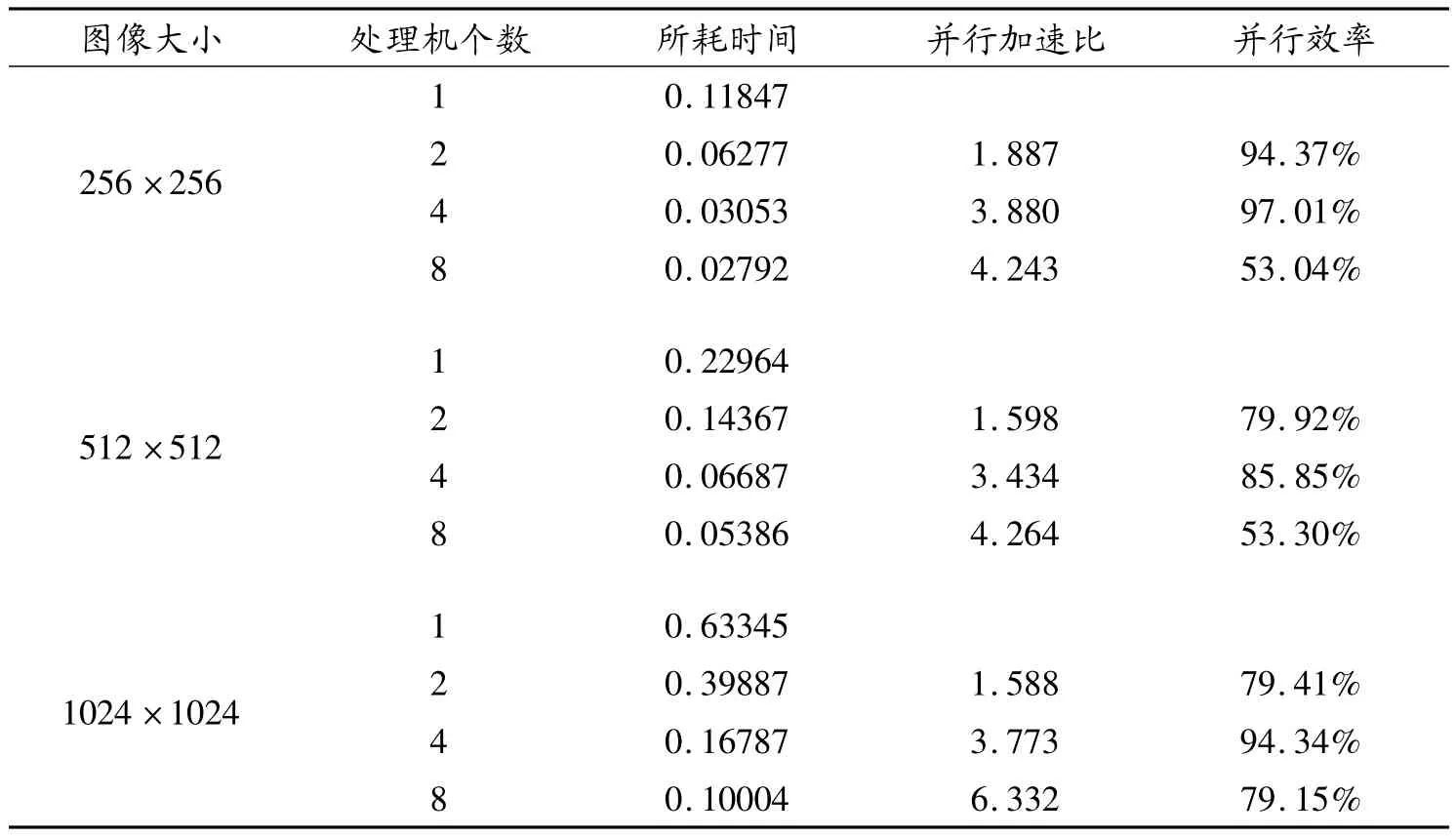
表1 图像FFT变换和IFFFT变换的测试结果

4 结语

通过对快速傅里叶变换并行化的研究发现，当数据量愈大时愈适合并行计算，而且它们的较大的加速比和较高的效率，但随着并行节点数的增加，并行加速比在增加，但效率在达到一个较大值后随之降低.

［1］［美］格拉法科斯.傅里叶分析(英文版)［M］.北京：机械工业出版社，2006.

［2］冷建华.傅里叶变换［M］.北京：清华大学出版社，2004.

［3］蒋长锦，蒋勇.快速傅里叶变换及其C程序［M］.合肥：中国科学技术出版社，2004.

［4］薛利敏，舒尚奇.利用行列式性质求矩阵的特征值［J］.渭南师范学院学报，2010，25(2)：13-14.

［5］H.J.Siegel.Report of the Purdue Workshop on Grand Challenges in Computer Architecture for the Support of High Performance Computing［J］.Journal of Parallel and Distributed Computing，1992，16(3)：199-211.

［6］史凤丽.基于集群计算机的图像并行处理［D］.西安：西安科技大学硕士论文，2010.

Research on Parallelization of Fast Fourier Transformation

ZHAO Xiao-lei，WANG Min
(School of Mathematics and Information Science，Weinan Teachers University，Weinan 714000，China)

This paper studies Fourier Transformation and its applied form，Fast Fourier Transformation(FFT).Meanwhile，the parallelization algorithm of image processing based on FFT is introduced in the paper.The results of the parallelization stimulation indicate that the larger amount of data is more suitable for the parallelization computation.The effect of the parallelization is not obvious when the processing node reaches a certain amount.

Fast Fourier Transformation;image processing;parallelization

O174.2

A

1009—5128(2011)12—0027—04

2011—05—26

渭南师范学院研究生专项项目(11YKZ014)

赵晓雷(1978—)，男，河南洛阳人，渭南师范学院数学与信息科学学院讲师，硕士.研究方向：图形图像处理.

［责任编辑 牛怀岗］