双锥流量计气液两相流测量模型研究

朱 跃,谢代梁,陶 姗,梁国伟

(1.中国计量学院计量测试工程学院,浙江杭州310018;2.杭州职业技术学院友嘉机电学院,浙江杭州310018)

在动力、化工、制冷、石油工业等中广泛存在着密闭管道气液两相流流动的工况,由于管道内气液两相流动存在可随流动变化的相分界面[1],使得气液两相流流量的准确测量难度很大.为了解决两相流流量测量问题,近些年来很多新的测量方法不断地涌现[2-6],虽然这些方法大部分仍处于实验阶段,但这些研究成果为深入研究气液两相流参数测量提供了很好的借鉴.

采用传统的单相流流量计结合相应的测量模型对气液两相流流量进行测量,是目前气液两相流参数检测研究中的重要方向之一,其中差压式流量计中的标准孔板或文丘里管被广泛采用,常用的流量测量模型包括:均相流模型和分相流模型以及基于均相流模型或分相流模型基础之上建立的 James模型[7]、Murdock模型[8]、林宗虎模型[9]等.这些模型在其实验范围内均具有一定的测量精度,但将测量模型推广到其他差压式流量计中,仍需对这些模型进行深入分析,对其中的一些参数进行修正.如:Zhiyao Huang等[4,5]采用文丘里管结合空隙率测量的方法对气/水和油气两相流流量测量模型的修正;Feng Dong等[10]采用实验标定的方法对V锥流量计的气/水两相流流量测量模型的修正.我们在V锥流量计的研究基础之上设计了一种直径比为0.8的双锥流量计,在50 mm管径的水平管上对气水两相流流量的测量进行了实验研究.通过对均相流模型平均密度修正的方法建立了适用于双锥流量计的气液两相流测量模型.

1 双锥流量计测量原理

1.1 双锥流量计节流装置结构

V锥流量计是20世纪80年代出现的一种新型差压式流量计.相比于其它传统差压式流量计(如孔板和文丘里管),V锥流量计在压损、重复性、量程比、长期工作稳定性等方面均表现出一定的优势[11],使得近些年来对V锥流量计的研究也逐渐增多.我们基于V锥流量计设计了一种新型双锥流量计,具有结构简单、压力损失更小等特点[12],但是作为一种新型内锥流量计,其能否应用于气液两相流量测量有待于深入研究.

双锥流量计和V锥流量计一样也属于边壁收缩、逐渐扩散式流量计.图1为双锥流量计节流锥体实物图,其节流锥体主要包括两部分:锥体和锥体支架结构.双锥流量计的锥体由前后两锥角相等的对称锥体组成;锥体支架结构有三个片状支架和一管环组成,锥体的支架结构通过锥体中间喉部将锥体固定在管道中心与管道同轴,其中管环的内径和管道的内径一样,将锥体安装在管道中就可以构成双锥流量计.

图1 双锥流量计节流锥体实物图Figure 1 Cone of the double-cone flowmeter

图2为双锥流量计的基本工作原理图.其中箭头代表的是流体流动的方向;P1、P2、P3分别为三个取压口,其中 P1口为上游流体收缩前静压取压孔,P2口为节流件喉部最小流通面积处静压取压孔,P3口为下游流体流束稳定时的静压取压孔;P1与P2之差为本研究中所取得双锥流量计差压信号;P1与P3之差为双锥流量计的另一组差压信号,其具体用途还有待于进一步研究;D为管道内径,d为节流锥体在喉部处直径.

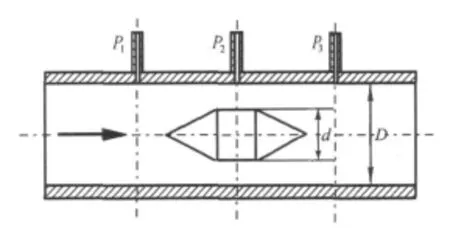
图2 双锥流量计工作原理图Figure 2 Structure of double-cone flowmeter

2 双锥流量计测量两相流的理论模型

2.1 双锥流量计单相流测量模型

在同一密闭管道中根据能量守恒原理(伯努利方程)和流动连续性方程可得,单相流的质量流量和差压之间的关系式为

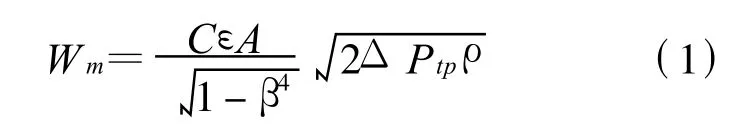
2.2 双锥流量计气液两相流测量模型

在单相流流量测量模型基础之上,均相流模型假设气液两相流流体在管道中均匀混合,则可以得到气液两相流的平均密度为

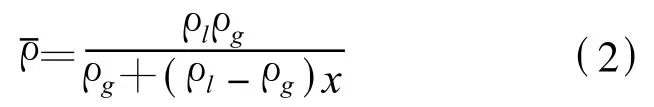
将(2)式中的平均密度代入(1)式则可得到均相流两相流流量计算模型为

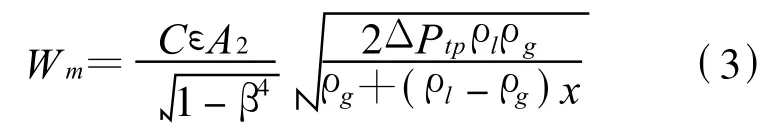
式(3)中ρl为液相密度,ρg为气相密度,ΔPtp为混合两相流同时流过节流装置的差压,x为气相质量含量即干度.

均相流模型假设气液两相混合均匀,为一理想模型,在实际应用时得到的测量误差往往较大,因此在应用的过程中常常需对其进行相应的修正.James[7]在工况压力为0.51～1.87 MPa,干度为0.01～0.56;孔口直径为14.2～16.8 mm;管道内径为20.05 mm的实验条件下,通过大量实验总结出汽/水两相流的均相流修正模型为

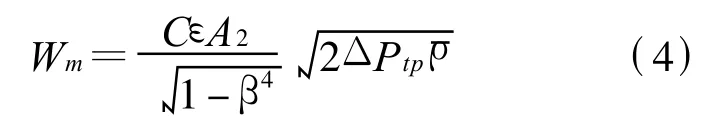
其中

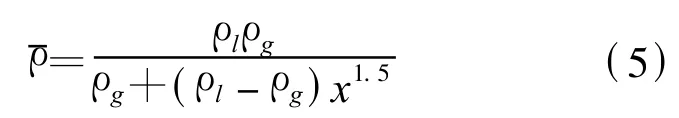
基于James模型对均相流模型的修正的思想,假设平均密度

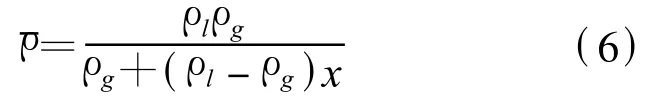
式(6)中x为干度x的函数.将(6)式进行等价变换得

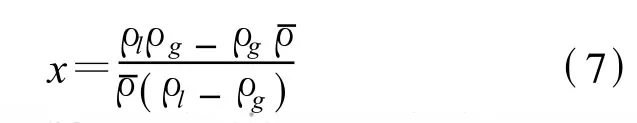
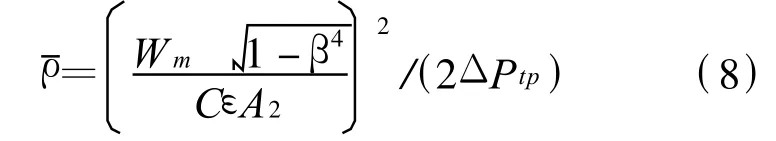
根据计算得到的X值与干度x建立相应的关系式

将(6)式和(9)式代入(4)式即可建立适用于双锥流量计的气液两相流均相流流量测量模型为

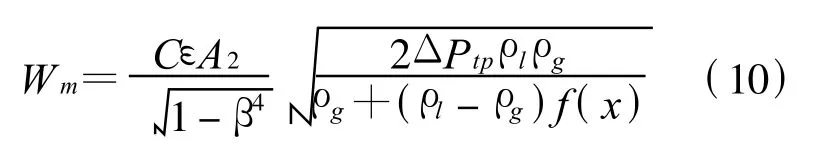
3 实验和实验结果分析

3.1 实验装置

双锥流量计气液两相流流量测量实验是在中国计量学院油气水三相流实验设备上进行的,研究中仅对水平管道气水两相流的测量进行了实验.实验设备主要包括数据采集系统和实验管路两大部分,其中数据采集系统包括数据采集器以及数据采集控制界面;实验管路包括压力变送器、温度变送器、差压变送器、标准表以及管道和阀门等设备,装置的结构如图3所示.

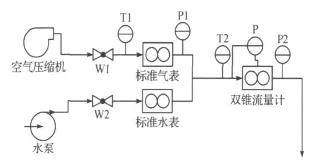
图3 气液两相流实验管路结构示意图Figure 3 Structure of gas/liquid two-phase flow pipeline

图3中W1,W2为球阀;T1,T2为温度变送器;P1,P2为压力变送器;P为差压变送器.

本次实验的介质为空气和水;采用电磁流量计作为液相标准表,采用旋进漩涡流量计作为气相标准表,精度等级均为0.2级;实验管道内径为50 mm,实验所用的双锥流量计等效内径比β=0.8;工况压力为 40～200 kPa,温度为27 ℃,干度范围为0.002 5～0.04;数据采集器采用的是研华公司的PCI-1710L,数据采集控制界面的开发选用的是NI公司的Labview软件,本次实验数据采集频率为1 000 Hz,采样时间为30 s.

3.2 流出系数标定

双锥流量计不是标准节流装置,在使用之前必须要对双锥流量计的流出系数进行标定.具体标定关系式为

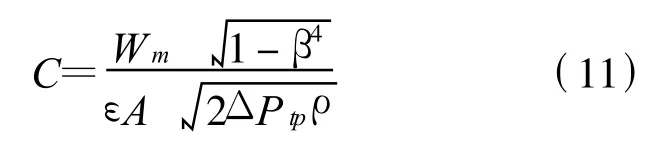
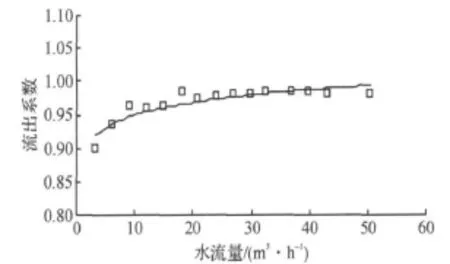
图4 用水标定流出系数Figure 4 Discharge coefficient

采用水作为流动介质,在液体流量标准装置上对双锥流量计的流出系数进行标定(标定时,水的密度为996 kg/m3,ε=1),根据文献[13]对流出系数和雷诺系数的研究可知流出系数随雷诺系数的变化而变化的范围不是很大,所以也可以用流出系数的平均值作为流出系数.图4为双锥流量计流出系数和流量之间的关系.经计算得双锥流量计流出的系数平均值为0.967 7.

3.3 测量模型建立

双锥流量计的气液两相流流量测量模型的建立通过以下几个步骤来实现:

2)建立干度确定式(9)中X和干度x的关系式,图6显示的为X和干度x之间的关系

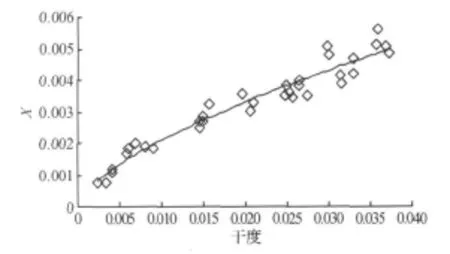
图5 X和干度x之间的关系Figure 5 Relationship X and mass fraction x

由最小二乘法拟合得X和干度(x)之间的函数关系式为

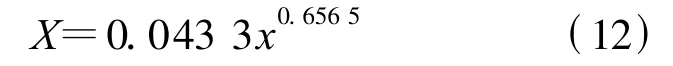
3)将(12)式代入(11)式确定双锥流量计的气液两相流流量测量模型为

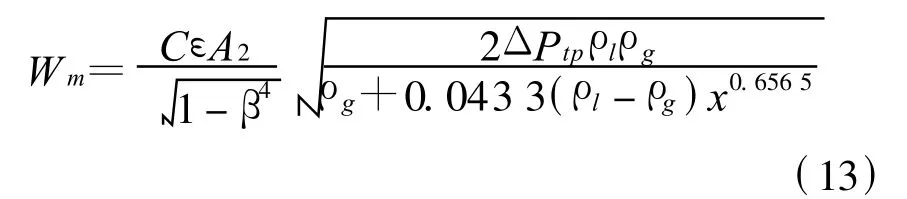
3.4 测量误差分析

为验证所建立的双锥流量计的气液两相流流量测量模型和修正前的模型相比是否有效,需要对所建模型的测量误差进行分析.本文选用总质量流量的相对误差和均方根误差作为评价标准.

将实验所得数据再代入到(13)式,计算其修正后的新模型测量误差,建立新模型测量误差和干度之间的关系图.为了便于比较分析,本文分别建立了干度 x和修正前均相流模型测量误差以及干度x和James模型测量误差的关系.如图6、图 7、图 8.

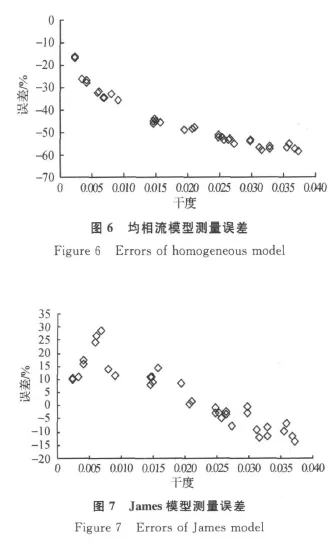
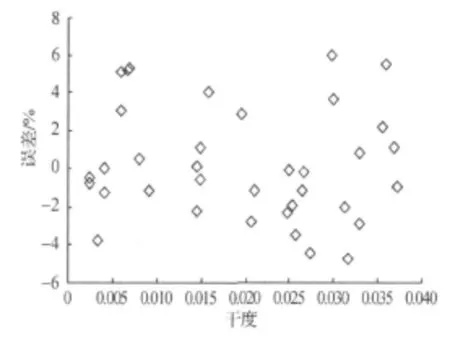
图8 修正后模型测量误差Figure 8 Errors of the proposed model

图6为均相流模型的干度和总流量测量误差关系,结果显示,在干度范围为0.002 5～0.04的工况下,均相流模型的总质量流量测量误差随干度的增大而增大,测量误差在10%～60%之间,经计算可得其均方根误差为54.77%.理论上来讲,均相流模型适用各种差压式流量计的两相流量测量,但是由于其假设过于理想,而实际工况难以实现气液两相完全充分混合,这就导致计算平均密度产生较大误差,而且随着气相含率的增加平均密度的计算误差越大,所以其测量误差较大并且随着干度的增加而增大.

图7为James模型的干度和总流量测量误差关系,结构显示:在实验干度范围内,James模型的总质量流量测量误差随干度的增加先减小再增大,测量误差可控制在30%以内,当干度小于0.02时其测量误差为正,当干度大于0.02时测量误差为负,经计算可得其均方根误差为12.72%.本次实验研究所在的工况和James实验工况有较大的区别,而且James模型是基于孔板差压信号建立的其信号和双锥流量计还存在一定区别,所以,将James模型直接应用于本次实验研究可能超出了James模型的适用范围使得James模型在本次研究中存在较大的测量误差.

图8为干度和修正后模型测量误差之间的关系,结果显示,修正后的模型测量误差较稳定,测量误差和干度没有明显规律性,修正后模型测量相对误差可控制在6%之内,经计算可得其均方根误差为2.94%.

4 展 望

本文仅对等效内经比为0.8的双锥流量计的气液两相流进行实验研究,所提出的模型修正方法能否应用于其它等效内径比的双锥流量计甚至是其它类型的差压式流量计,还有待于进一步的实验研究.

本文是在干度范围为0.002 5～0.04的工况下建立的模型,在其他工况条件下,本文所建模型有可能不再适用,此时需要按照前面模型构建方法对模型进行重新构建,可以采用分段建模的方法来扩大模型的适用范围.

5 结 语

将一种新型双锥流量计应用于气液两相流量测量研究.在中国计量学院油气水三相流实验设备上进行了流量测量实验,获得了等效内径比β=0.8的双锥流量计的气液两相流的流量系数为0.967 7.

在均相流模型的基础上,提出了一种均相流平均密度修正的方法,建立了双锥流量计气液两相流流量测量模型.

通过对总流量测量相对误差及均方根进行分析可知,在本次实验研究工况范围内,双锥流量计的修正后的模型的测量误差可控制在6%之内,均方根误差为2.94%,与修正前的均相流模型以及James模型相比其测量特性有了很大的提高,表明本文所提出的修正方法对双锥流量计而言是有效的.

[1]林宗虎.气液固多相流测量[M].北京:中国计量出版社,1988:1-92.

[2]WANG W R,TONG Y X.A new method of two-phase flow measurement by orifice plate differential pressure noise[J].Flow Meas Instrum,1995,6(4):265-270.

[3]KOJASOY G,LANDISP F.KWAME-MENSA H P.et al.Two-phase pressure drop in multiple thick and thin-orifice plates[J].Ex perimental Thermal and Fluid Science,1997,15(4):347-358.

[4]HUANG Z Y,XIE D L,ZHANG H J,et al.Gas-oil twophase flow measurement usingan electrical capacitance tomography sy stem and a Venturi meter[J].Flow Measurement and Instrumentation,2005,16(2,3):177-182.

[5]M ENG Z Z,HUANG Z Y,WANG B L,et al.Air-water two-phase flow measurement using a Venturi meter and an electrical resistance tomography sensor[J].Flow Measurement and Instrumention,2010,21(3):268-276.

[6]王 芳,梁国伟.环形管流量计测量气液两相流研究[J].中国计量学院学报,2006,17(2):103-106.

[7]JAMES R.Metering of steam-water two-phase flow by sharp edged o rifices[J].Proc Inst Meech,1965,180(23):594-566.

[8]M URDOCK J W.Two-phase flow through measurement with orifices[J].Journal of Basic Engineering,1962,84(4):419-433

[9]LIN Z H.Two-phase flow measurement with sharp-edged o rifices[J].International Journal of Multiphase Flow,1982,8(6):683-693.

[10]DONG F,HU J.Study of the gas-liquid two-phase flow measuring method based on the V-cone flow meter[C]//The 5th International Symposium on Measurement Techniques for Multiphase Flows.Macao:American Institute of physics,2007,207-214.

[11]IFFT S A,MIKKELSEN E D.Pipe elbow effects on the V-cone flowmeter[C]//Fluid M easurement and Instrumentation Forum.Washington:Tluid measurement and Instrumention Forum,1993:37-41.

[12]梁佳娜,梁国伟,沈平平.双锥流量计实验研究与计算模拟[J].中国计量学院学报,2010,21(3):201-205.

[13]SINGH S N,SESHADRI V,SINGH R K,et al.Effect of upstream flow disturbances on the performance characteristics of a V-cone flowmeter[J].Flow Measurement and Instrumentation,2006,17(5):291-297.