玉溪市未来人口预测三种模型的分析

柳德江 殷凤玲 唐红燕

(1．玉溪师范学院资源环境学院，云南玉溪653100;2．玉溪师范学院信息工程学院，云南玉溪653100)

玉溪市未来人口预测三种模型的分析

柳德江1殷凤玲2唐红燕1

(1．玉溪师范学院资源环境学院，云南玉溪653100;2．玉溪师范学院信息工程学院，云南玉溪653100)

人口问题是一个国家或地区可持续发展的前提。人口规模是否合理，对一个国家或地区未来的经济、社会和生态环境可持续发展影响深远。运用马尔萨斯人口模型、Logistic增长模型和线性函数三种理论模型，利用《玉溪市统计年鉴》统计数据对玉溪市2010—2020年的人口发展规模做出预测，预测结果显示3种模型均取得了较好的模拟效果。Logistic增长模型的预测值最小，故采用其预测值作为预测结果。

人口预测;Malthusian模型;Logistic增长模型;线性函数;玉溪市

玉溪市位于云南省中部，区位优越，经济发达，在云南经济发展中具重要地位。玉溪市未来人口规模是否合理?不仅影响到玉溪市未来经济和社会发展，而且会影响到资源、环境的可持续发展，因此准确地预测玉溪市户籍人口的发展趋势，对于制定合理的人口规划和人口布局方案具有重大的现实意义。

1 玉溪市历年人口发展趋势分析

玉溪市人口发展经历了三个变化过程:一是20世纪70年代末期到80年代中期，随着人口出生水平下降，实现了人口年龄结构由年龄型向成年型的初级转变;二是20世纪90年代，人口年龄结构实现了由早期的成年型向成年型晚期的转变;三是21世纪初期，人口年龄结构实现了由晚期的成年型向老年人口年龄类型的转变。

2 三种预测模型的比较

根据玉溪市2001－2009年的户籍人口统计数据来建立模型，采用马尔萨斯人口模型、logistic模型和线性函数3种方法的来验证模型，并预测玉溪市2010－2020年的总户籍人口数。

2．1 马尔萨斯人口模型

英国人口学家马尔萨斯(T．Malthus)根据百余年的人口统计资料，于1798年提出了著名的人口模型，是基于几何级数增长的模型。这个模型的基本假设是:人口的增长率是常数，即随着时间的增加，人口按指数规律(几何级数)无限增长。其计算公式为［1］:

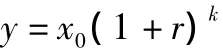
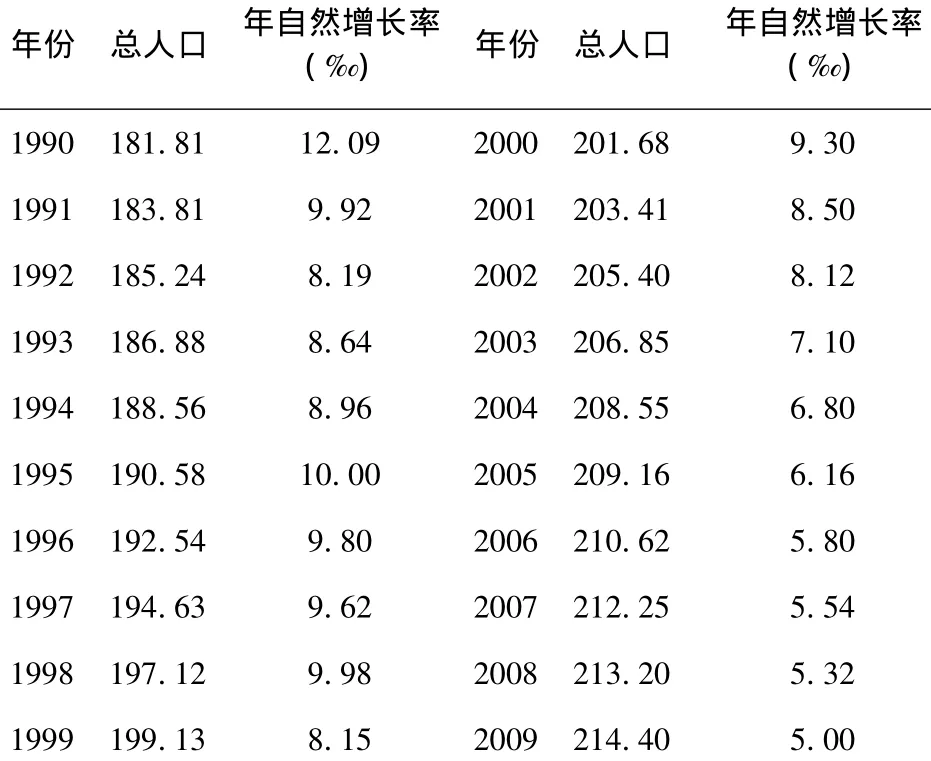
表1 玉溪市1990－2009年人口数量变化(万人)

其中:x0为初始年人口数，r为年增长率，k为预测年限;玉溪市1990－2008年的年平均人口自然增长率为8．47‰，采用高、中、低3个方案预测。2010－2020年玉溪市的总人口数。其中，高方案采用的人口自然增长率保持1990－2000年的最高值12．09‰;低方案采用人口自然增长率为1990－2009年的最小值5．00‰;中方案取其平均值8．47‰。

以2000年为基期，根据马尔萨斯人口模型，可以得到玉溪市2001－2020年总人口的高、中、低三种不同方案的预测值。比较上述三种方案，低方案比较保守，预测结果偏低，高方案的预测结果偏大，中方案预测结果介于两者之间，预测结果适中。综合认为中方案的预测结果比较符合玉溪市未来人口发展的动态趋势(见表2)。

2．2 Logistic增长模型

Logistic函数适用于无法进行因素预测的小区域人口预测，且预测期不宜过长。其方程形式为［1］:

这一函数也称为逻辑斯蒂(Logistic)曲线，Pt为第t年的人口规模;Pm为人口极限规模;α、β都为计算系数。逻辑斯蒂(Logistic)曲线的含义为:在人口发展的早期人口总量的增长速度虽快，但人数增加不多，以后人口增长速度不断放慢，每单位时间增加的人数也逐渐减少，最后人口规模接近最高值Pm。

拟合逻辑斯蒂(Logistic)曲线的准则是:若令 k=1/pm，a=eα/pm，b=e－β，则 1/pt=k+abt。当 t取等间距时，对应Pt的倒数(1/Pt)的相邻项的差值为:y=1/pm+n+－1/pm，它们相邻项之间的比值按定值b变化。

用该函数预测人口总数时，要根据预测地的历史数据拟合出该函数的曲线方程。即:选择三个等间距的点(P0、P1、P2)，每点相距n年，这样就组成方程组:

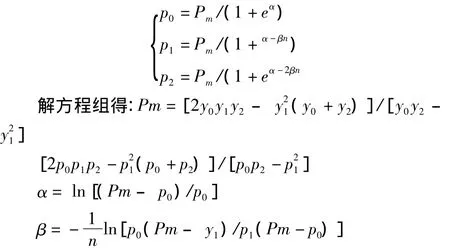
根据公式及拟合原则，以1990－2009年玉溪市人口统计数据为基础，发现历年人数在增加，而历年人数的倒数的相邻项的差值几乎按等比变化(比值在0．8～1．0之间)，所以可以使用Logistic函数来预测。若按5年间距选取1995年、2000年、2005年的三个人口数据，则通过计算得:Pm=222．27，α = －1．79，β =0．098，故拟合的 Logistic函数模型如下:

y=222．27/(1+e－1．79－0．098t)

其中，pt表示人口数量(单位:万人)，t为年份长度。

2．3 线性函数模型

假设该地平均每年人口按某一固定数值变化，然后用以下线性方程来求解［1］:

pt=p0(1+rt)

其中，Pt为预测t年人口数;P0为基期人口数，r为人口年均增长数，t为预测年限。根据历年数据得年均增长率 r为 0．0093。

2．4 模型的验证情况

利用玉溪市1990－2009年统计数据建立预测模型，预测2010－2020年的人口发展规模，通过误差的对比分析(见表2)，得到线性函数的平均相对误差为0．82%，马尔萨斯人口模型的平均相对误差为0．52%，而Logistic增长模型的平均相对误差为－0．23%，说明三种模型均能较好的模拟预测。但从各自的相对误差来看，发现马尔萨斯人口模型前面几年预测的误差很小，但随时间的延续误差在逐渐增大;线性函数也是随时间延续相对误差在逐渐增大，但两者相比马尔萨斯人口模型预测的结果误差相对要小;而Logistic增长模型预测的误差值比前两者都要小，且误差的变化范围不大。因此，采用Logistic增长模型的预测值作为玉溪市未来的人口预测值是可行的。

2．5 未来人口规模的预测结果

采用Logistic增长模型预测2010－2020年玉溪市户籍总人口达到219．11万人，增长数量较为稳定，增长速度较为缓慢，将逐渐过渡到零增长。

表2 玉溪市总人口三种模型的预测值及误差(万人)

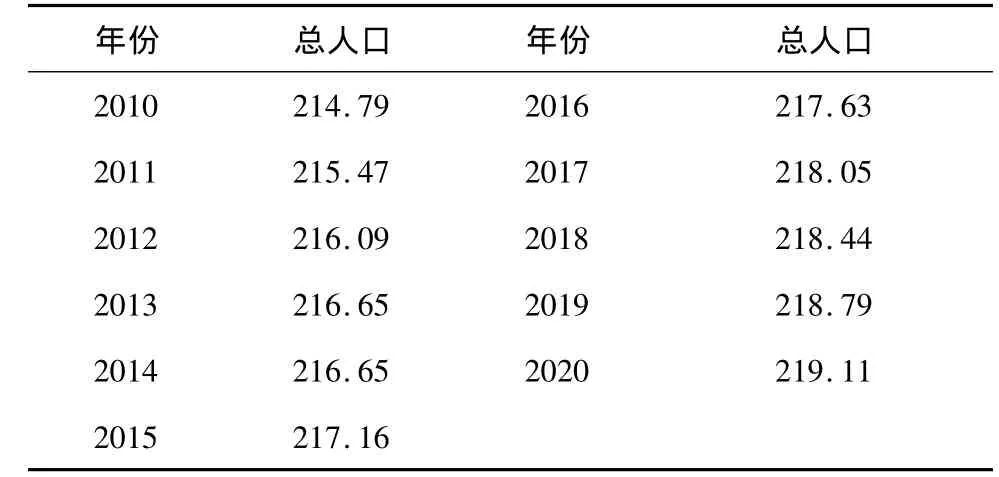
表3 2010－2020年玉溪市人口规模的预测值(万人)

3 结论和建议

3．1 三种模型的比较分析

比较上述三种模型在本研究中的模拟及预测结果，可以得出以下结论:

(1)线性函数模型、马尔萨斯人口模型和Logistic增长模型均取得较好的预测效果。

(2)线性函数模型与另两种模型相比，预测精度略低，但在实践操作中更为直观，而且简便易行，更宜运用在基层或是要求精度较低的预测中。

(3)马尔萨斯人口模型和Logistic增长模型，在本研究中体现了较高的精确性和两者相近的预测结果，更适宜运用在要求较高的专业研究中。

人口增长受多种因素的影响，任何一种模型都不能完整地预测其发展情况，具体采用何种模型，应该按照实际情况加以选择，如能将各种定性和定量模型有机地结合将是比较理想的预测方法。

3．2 预测结果及建议

从以上预测结果来看，玉溪市户籍人口将会持续稳定增长，但增长速度缓慢，自然增长率持续下降。未来十年内，在实现稳定低生育水平的前提下，玉溪市人口将维持在低增长状态，从而为实现现代化和可持续发展创造有利的条件。但随着人口的持续增长，劳动就业压力会进一步加大，人口老龄化问题将会更加突出，人口与经济、社会、资源和环境之间的矛盾依然尖锐。总之，实现玉溪市社会经济的可持续发展，要把人口工作的重点放在以下四个方面:控制人口数量、提高人口素质，加大扶贫力度;加快推进人口城镇化、优化人口结构;实施劳动力转移，缓解资源环境的压力;建立可持续的消费模式。

(编辑:于 杰)

［1］张善余．人口地理学概论［M］．上海:华东师范大学出版社，2004:442－449．

［2］哈斯巴根．通辽市未来25年人口预测与分析［J］．内蒙古师范大学学报:自然科学汉文版，2006:248－252．

［3］瞿振武，刘爽，段成荣编．常用人口统计公式手册［M］．北京:中国人口出版社，1993:10－13．

［4］邹自力，刘珊红．人口预测方法及可靠性探讨［J］．华东地质学院学报，2002，25(2):142 －146．

［5］玉溪市统计局．玉溪市统计年鉴［M］，北京:中国统计出版社，2007:32－37

Analysis on Three Prediction Models to Future Population in Yuxi City

LIU De-jiang1YIN feng-ling2TANG Hong-yan1
(1．College of Resources and Environment，Yuxi Normal University，Yuxi Yunnan 653100，China;2．College of Information and Engineering，Yuxi Normal University，Yuxi Yunnan 653100，China)

Population is the sustainable development premise of a country or a region，so whether population size is reasonable or not has great influence on the sustainable development of economy，society and environment in a country or a region in the future，thus predicting the development of population becomes necessiavy．The population development during 2010 to 2020 of Yuxi city is predicted in this study by applying three theoretical models:Malthus population model，Logistic growth model and linear function，and the population data of“Yuxi Statistical Yearbook”as well．The results of study show that all of the three models obtain good simulated effects，the average relative error of the three are small in the model verification process．Since the minimal value appears in the Logistic growth model，its predictive value is taken as the result．

population prediction;malthus models;logistic models;linear function;Yuxi

K901．3

A

1002－2104(2011)03专－0017－03

2010-08-08

柳德江，讲师，主要研究方向为人口、城市地理、区域可持续发展。

云南省教育厅基金项目资助(编号:08Y0298)。