高斯分布模拟X射线相干散射能量分布的研究
刘太辉,刘景鑫,宋建中,李艳红
1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130013;2.北华大学 计算机学院,吉林 吉林 132031;3.吉林大学中日联谊医院 信息中心,吉林 长春 130033
高斯分布模拟X射线相干散射能量分布的研究
刘太辉1,2,刘景鑫3,宋建中1,李艳红2
1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130013;2.北华大学 计算机学院,吉林 吉林 132031;3.吉林大学中日联谊医院 信息中心,吉林 长春 130033
专栏——医学影像设备新技术的研究与应用
编者按:研究创新的医学成像设备与技术、开发现有医学影像设备的新功能,推广应用新技术,是我们临床医学工程人员的重要工作,需要临床医学工程人员与医疗、技术和护理等多方面人才的密切合作。本期专栏主要探讨创新的医学成像技术研究及医学影像设备新技术开发应用等问题。

栏目主编:刘景鑫
刘景鑫,教授,硕士生导师,吉林大学中日联谊医院信息中心主任,吉林省医学影像工程技术研究中心主任,吉林省医学影像质量控制中心副主任,中华医学会医学工程分会常委,《中国医疗设备》常务编委。主持多项国家自然科学基金及省市科技攻关项目。
X射线的相干散射图样呈高斯分布,本文通过高斯分布的理论模拟理想状态下的散射分布图样,在此基础上进一步模拟噪声影响和偏心影响,从而推断出试验图像中分布特征的本质,为后期的分析工作提供依据。
X射线;高斯分布;相干散射;能量分布;康普顿散射
X射线相干散射本质上是对非固定晶体构型物体中不同的物质成分的衍射。大量的实验证明,X射线的相干散射线反映了物体内同一物质同一分子内不同原子电子之间或者不同分子之间同一物质成分原子电子之间的相干特征,这种特征在沿着X射线入射线束方向上很小的角度上分布(<10°)。由于散射线具有与物质成分相关的特征,因此相比较传统的X射线透射诊断,散射线在分子结构上反映了物质成分的存在、多少及变化信息,提供了更加准确的分子量级上的物质成分信息,可以有效地提高X射线诊断的准确性。
近些年,相干散射逐渐开始应用到医学上,用来分析生物物质成分的重要信息。例如Puumalainen等人计算确定的电子能量条件下,相干散射和90°角度上的康普顿散射之间的比率,来确定骨骼内的矿物质密度[1]。同时,人们通过灰烬法和组织形态计量学方法证明了单纯地测定相干散射截面的方法也可以准确地测定骨骼矿物质的含量[2-3]。大量的事实证明通过相干散射测定法比放射学法、光子吸收方法和定量CT更加准确地测定骨骼矿物质含量[3-4]。文献[5]中证实了像骨骼和脂肪的散射截面是截然不同的。特别是羟磷石灰具有多晶体的结构特征,在健康的骨骼内和骨质疏松的骨骼内截面特征是完全不一样的[6]。其他的应用还有乳房组织的相干散射分析,不同的乳房组织(癌组织、纤维组织、脂肪等)的散射截面峰值出现在不同的散射角度上[7]。这些应用上的研究,都充分地证明了X射线相干散射在生物物质成分分析中有着巨大地应用潜力。
上述的应用研究,都假定是基于单色的X射线源光谱进行的。实际上,所谓的单色只能够是近似的单色。除了大型的加速器可以获得绝对单色的X射线光子以外,其他的单色光谱都是一定程度的近似。实际应用中,临床的X射线源绝大多数是钨靶材料的,其光谱近似于白光谱,而且没有明显的峰值。好一点的光源是钼靶材料的,其峰值很明显,但是也是具有一定的谱宽分布的。因此,使用临床影像设备获得的相干散射信息都是基于白光光源的,而且其照射时间受设备条件的限制小于2s,如果不采用密封的屏蔽设备,那么空间中的杂散射线会是主要的干扰源。
这里,我们使用临床的X射线影像设备,对样品进行X射线相干散射成像。图像的分布理论上是围绕射线束的同心圆环。基于上面的分析,这些圆环将被虚化,空间角度上的分布将呈现出高斯分布的特征。文中使用高斯分布模拟水样品的相干散射图像,同时对基于图像分析算法的特征分布曲线上的一些问题进行模拟和说明。
1 X射线相干散射图像的特点
微观上,相干散射的本质是同一种类物质原子外层电子对入射X射线的衍射。Harding[8]在他的研究中认为,对于相干散射的研究应该归结为两类:一类是在单色光源的条件下,研究相干散射线在空间中的角度分布特征;另一类是在白光光源条件下,固定某一个空间角度,分析和研究多光谱的相干散射特征。而在实际的临床条件下,唯一有效的探测手段就是X射线的放射影像技术,目前最先进的DR条件下的影像环境完全可以对物体进行有效的相干散射成像。但是,对于获得的图像由于其具有白光光源条件,而又是在空间角度上一次性成像,如何进行分析是进一步研究工作的基础。
Westmore在研究中使用纯铝粉来模拟多晶、白色光源条件下的相干散射现象,发现多晶条件下相干散射光谱图像的分布不再是单色、单晶条件下的脉冲图样,而是具有一定的分布宽度的高斯分布。该高斯分布主要来自于白光光源的不同波长X射线相干散射之间的“线性叠加”[9]。由此可以明确,临床影像设备获得的图像必然是基于高斯分布的具有一定分布宽度的光谱图像。
图1是水样品的相干散射图像。靶材料:钨;成像探测器DR。样品与探测器之间的距离40cm、电压90kV。由于纯水样品可以看作单一物质样品,白光条件下其分布是具有一定宽度的高斯分布。在相干散射图1(a)中,其分布不易被看出来;在图1(b)中通过空间分布的能量曲线可以明显地观察到整体的分布是一个高斯分布。图1(b)中的曲线分布并不是完全的正态分布,曲线上面有严重的高频毛刺叠加。该曲线是经过处理后的曲线,在原始的分布曲线中图1(c)还存在着分布曲线随着角度的增大而呈现梯度增加的现象。

图1 a.水样品的相干散射图像;b.水样品相干散射能量空间分布曲线图;c.未经过处理的相干散射能量分布曲线图。
2 高斯分布的模拟
如果使用高斯分布模拟相干散射现象,可以使用这样的高斯分布函数:

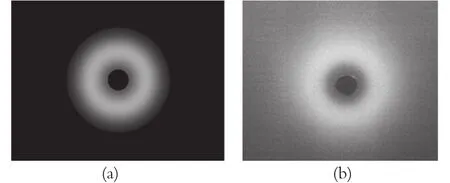
图2(a) 高斯分布模拟图;(b) 水样品的相干散射图
这里 μ是平均值,δ2标准偏差。对于一个标准的正态分布,μ= 0 and δ2= 1. 任何其他类型的正态分布都可以看作是标准正态分布在水平方向上按照系数δ的拓展,然后向右侧偏移距离 μ。这里构建正态分布时,以图像的正中心为圆心,以象素点的平方和作为在某一个直径的圆环上的能量。如图2所示,
3 能量分布对比
对于模拟的高斯分布和实验的相干散射图像,我们都采取同样的方法来计算它们的能量分布。即假定他们的分布都是同心的圆环,模拟的图像圆环圆心已知,而对实验图像则需要求解近似的圆心,然后计算能量分布曲线。

这里Vj是半径为ri的圆环上图像象素的灰度值。以圆心为起点,对不同的半径的圆环上的像素灰度求其平方和作为该圆环的能量,得到的就是空间能量分布。
很显然,由于没有任何的噪声干扰,高斯分布图像提取的曲线如图3(b)所示,完整地再现了理论正态分布的样子。而对于相干散射图像获得的能量分布曲线,则存在着:① 峰值偏移,不在分布的正中位置;② 曲线上有高频的毛刺叠加;③ 如图1(c)所示。而且不经处理的能量曲线,有一个直流分量、沿着空间角度的增大而呈梯度增加如图1(c)所示。
产生上述不同的原因,从相干散射的机理上应该主要来自于:① 非相干散射(康普顿散射);② 噪声;③ 经过算法确定的同心圆环的圆心偏心。
4 高斯分布图增加噪声影响
这里把X射线相干散射过程中所有的噪声多归结为白噪声的影响:
Val(randx,randy)=Valcurrent+255xVrand (3)
这里Val(randx,randy) 是图像中随机选中的像素点的灰度值, Valcurrent 是图像附加噪声影响前的灰度值, Vrand 是归一化的随机噪声值。
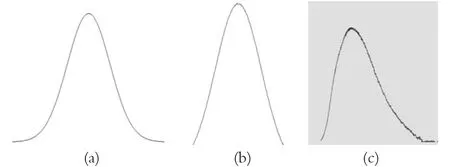
图3 (a) 理论正态分布曲线;(b) 从高斯分布图像提取的能量分布曲线;(c) 从相干散射图像提取的能量曲线
这里为了描述噪声对图像的影响,定义信噪比如下:

Nwhole是图像总体的像素数量,Nnoise是被噪声影响的像素数量。
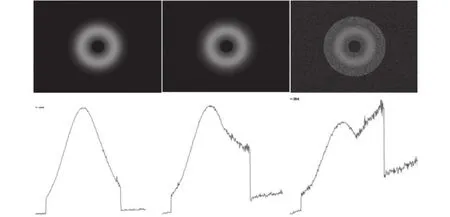
图4 不同的噪声干扰图像及其能量曲线 SNR(28dB,12dB,2dB)由左至右
如图4所示,附加噪声后,不同的信噪比条件下能量曲线的变化是不同的,随着噪声影响的增加,明显地会出现沿着半径向外辐射方向上能量曲线被抬高的现象。峰值也随着噪声影响的增加而幅值变小。而且受到噪声影响的轮廓是一条固定梯度的直线,这说明噪声影响是线性增加的。理论上,由于随机噪声是空间均匀分布的,而能量曲线的提取是以圆心为基点,沿着半径向外辐射的,随着半径的增加噪声的影响也是线性增加的。因此,这个直线轮廓的梯度可以反映出图像上随机噪声的影响程度,可以作为图像是否符合处理条件的判断依据。同时也可以发现,随机噪声的加入并没有影响高斯曲线的峰值位置,由此可以判断试验图像中峰值的偏移不是由白噪声引起的。
5 高斯分布图像的偏心模拟
由于分布图像的圆心为已知,因此获得的能量曲线与理论图像完全一致。但是试验图像的圆心是由算法估算得来,可以得到:① 试验图像圆心是近似的圆心,通过模拟偏心我们可以获得判别最优圆心的判据;② 通过偏心的模拟,我们可以判别准确圆心对能量曲线的影响。

图 5 曲线随着圆心的偏移而变化的图示
在提取能量曲线的过程中,有意地将圆心逐渐偏离准确圆心,然后采取相同的算法提取能量曲线。如图5所示,随着偏心的出现,能量曲线开始变化。首先,能量曲线上出现了高频的毛刺现象,这种现象随着偏心距离的增加而加重,并且毛刺的幅值在增加。但是能量曲线的整体轮廓并未受到影响,而且在偏心距离不是很大的情况下,能量曲线的峰值不受影响,峰值的位置也不受影响。当圆心偏心过大,例如圆心进入到有效的数据区内,能量曲线将严重受损。其次,能量曲线随着偏心距离的增加,能量曲线的底部开始变形,底部开口变大,曲线的最小和最大位置向两侧拉伸。
6 结论
由高斯分布模拟相干散射,可以从理论上解释一些试验图像上无法准确描述的现象。由文章的模拟结果可以发现,通过对相干散射图像进行能量曲线的提取是分析的一条可行方法。能量曲线峰值的强度反映了噪声干扰的多少;曲线轮廓中直流分量轮廓的梯度可以侧面反映噪声干扰的强度,通过梯度可以反向恢复曲线峰值信息;偏心会导致曲线上的高频毛刺现象。实际试验中的图像的毛刺是无法去除的,这说明通过同心圆环这个模式来解释相干散射的能量分布是一种近似,这与使用的射线束不均匀以及照射时笔束方向与探测器不绝对垂直有直接关系,可以通过寻优算法确定最优的圆心来提高曲线提取的准确性;偏心和噪声都不会改变曲线的峰值位置,这为分析提供了良好的理论支持;同时偏心和噪声也不会导致曲线的不对称现象,因此可以确定试验曲线中的不对称现象是由康普顿散射造成的,进一步的分析应该充分考虑康普顿散射的影响。
[1] P Puumalainen,A Uimarihuhta,E Alhava, et al.A new photon scattering method for bone mineral density measurements[J]. Radiology,1976,120:723-724.
[2] M Newton,D W L Hukins,G Harding.Bone composition measured by x-ray scattering[J].Phys.Med.Biol,1992,37: 1339-1347.
[3] S A Kerr,K Kouris,CE Webber,et al.Coherent scattering and the assessment of mineral concentration in trabecular bone[J].Phys Med Biol,1980,25:1037-1047.
[4] A M Ndlovu,T J Farrell,C E Webber.Coherent scattering and bone mineral measurement: The dependence of sensitivity on angle and energy[J].Med Phys,1991,18:985-989.
[5] J Kosanetzky,B Knoerr,G Harding,et al.X-ray diffraction measurements of some plastic materials and body tissues[J].Med Phys,1987,14:526-532.
[6] G Harding,J Kosanetzky,D Hukins,et al.Potential of x-ray diffraction computed tomography for discriminating between normal and osteoporotic bone[M].The Aging Spine,Manchester University Press,Manchester,1987:157-162.
[7] S H Evans,DA Bradley,DR Dance,et al.Measurement of smallangle photon scattering for some breast tissues and tissue substitute materials[J].Phys Med Biol,1991,36:7-18.
[8] G Harding,B Schreiber.Coherent X-ray scatter imaging and its applications in biomedical science and industry[J].Radiation Physics and Chemistry,1999,56:229-245.
[9] M S Westmore,A Fenster,I A Cunningham.Angulardependent coherent scatter measured with a diagnostic x-ray image intensifier-based imaging system[J].Med Phys,1996,23: 723-733.
Research of the Energy Distribution of X-ray Coherent Scatter by Gauss Distribution Simulating
LIU Tai-hui1,2, LIU Jing-xin3, SONG Jianzhong1, LI Yan-hong2
1. Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun Jilin 130013, China; 2. Computer College, Beihua University, Jilin Jilin 132031, China; 3. Information Center, China-Japan Union Hospital of Jilin University, Changchun Jilin 130033, China
The pattern of X-ray coherent scatter contributes a Gauss distribution. In this paper, the coherent scattering patter was theoretically simulated by Gauss distribution modal. On the basis of it, the affection of noise and eccentric were simulated, so the essential character of the distribution of experimental images has been deduced. These results provide the theoretical support for the later analysis.
Gauss distribution; coherent scattering; energy distribution; Compton scattering
TH774
A
10.3969/j.issn.1674-1633.2011.06.002
1674-1633(2011)06-0010-04
2011-02-01
国家自然科学基金(60372062)
本文作者:刘太辉,副教授。
刘景鑫,教授,硕士生导师。
作者邮箱:liujingxin@126.com

