基于椭球面大尺度表达地表对象方法研究

杨永崇，竞 霞

(西安科技大学测绘学院，陕西西安710054)

基于椭球面大尺度表达地表对象方法研究

杨永崇，竞 霞

(西安科技大学测绘学院，陕西西安710054)

针对传统地图投影理论在表达大区域或全球范围数字地图和GIS时存在的诸多问题，首次提出并论述椭球面数字地图和电子地图的概念及其优越性。借鉴传统地图投影理论表达地表对象的思想，提出利用曲面投影表达椭球面地表对象的思路，并在此基础上探讨椭球面电子地图的绘制、显示和分析的基本方法。基于椭球面表达地表对象，由于没有经过椭球面到平面的投影，因此可避免投影变形，并有效地解决大区域或全球范围数字地图和GIS的表达问题，拓展电子地图与数字地图的分析功能与应用范围。

地图载体;地图投影;大地坐标;数字/电子地图;椭球面

一、引 言

受传统地图学的影响，目前几乎所有的数字地图和GIS都是沿用传统的地图投影理论，并以此为空间数学基础，这在特定用途、局部范围内是可行的。但在大区域数字地图以较大区域甚至整个地球作为对象的情况下，地图投影会引起裂缝，并产生较大的几何变形，且地图投影的三要素很难限定。地图投影所定义的二维空间坐标度量是非线性的，即每个投影都有自己的坐标系，只有同样投影的地形图之间的坐标值才是可以比较和运算的。所以，当区域范围从小区域扩展为大区域或全球时，传统的投影已不能满足数字地球连续多变分辨率和全面用途的需要。此时采用地图投影为空间数学基础会带来诸多问题，使用起来具有诸多不便，主要表现在:

1)对于大区域，不能全局连续可视化，不能进行全区域统一的地理分析，这是根本性的缺陷。对于分带投影如此，对于大宽带而言，则变形太大且复杂，而且不规则，给后续工作和可视化带来很多困难和不良效果。

2)地图投影不适合多分辨率的定向结构和表示。在该投影下，定义全域准确的长度和度量十分复杂，实施较为困难;相应的，进行投影变换以统一空间数学基础则情况多变，也十分复杂和困难。

3)系统不便于动态变化和扩张。在时空及性质用途方面，一个区域的地理信息面临十分频繁的动态变化，如边界的外扩、合并，此时区域没有固定的边界，此外由于地图投影的复杂性，区域性，因此难以进行规范的分解合并工作［1］。

4)难以在二维度量空间中对三维空间和时间维进行定义。对于较大的区域，因不能再将地球看成水平面，所以将水准高程与投影平面上的高斯坐标作为地面点的三维坐标，就不能准确真实地表达地球表面的空间信息，特别是难以满足一些特定需求［2］。

当空间数据从局部向大区域甚至全球范围发展时，由于数字地图和GIS中的空间数学基础并没有得到相应的变化和发展，因此目前基于地图投影的数字地图和GIS已不能满足数字地球连续多分辨率和全面用途的需要。胡鹏等认为数字环境下空间数据产品在理论和实践上都遇到了空间数学基础问题，这也是整个地球空间信息科学发展中的基础问题［3］。建立一套适合于全球多分辨率、连续、精密、可视化量算的多维地球数据和标准框架下的统一空间数学基础，已引起国内外相关学者们的高度重视，但目前的研究重点主要是解决地球表面的表达问题，而较少涉及地球表面对象的表达。尽管在Google Earth中也表达了一些城市的少量中大比例尺矢量数据，但在整体与局部之间还没有建立任何关联［4］。

地图所反映的地理信息主要是地表信息，参考椭球面是最接近地球表面的可用数学方法表达的标准面，而用大地坐标与大地高联合描述在参考椭球面上的地理实体的几何形状是没有任何变形的。因此基于椭球面表达地表对象是最适合数字地球要求的地图表现形式，是分布式GIS数据无缝显示的最佳解决办法。它可以实现同地数据库或异地数据库之间不同数据层的无缝显示、不同比例尺的无缝显示和不同时相的无缝显示。所以，研究基于椭球面表达地表对象的理论与技术对数字地球的地图可视化、多维表示与动态显示具有非常重要的作用，并将有力地拓展电子地图与数字地图的分析功能与应用范围等。

当前基于椭球面表达地理信息的研究大多采用栅格或图像形式(如Google Earth用遥感影像来表达地理信息)，表达地球表面的模型大都采用栅格数据，而本文的研究则是用离散的形式或矢量数据表达地球表面对象。

二、椭球面数字地图

数字地图是在广阔的数学空间里表达地理信息，它在数学空间里将地图要素的每个点位均定位于某个投影系统中，或定位于某种椭球面上［5］，从而表示地理要素在真实世界中的几何形态和时空分布。这种定位于参考椭球面上以大地坐标定义地表对象空间位置的数字地图称为基于大地坐标的椭球面数字地图，简称椭球面数字地图。

1.基于椭球面的空间点定位方法

基于椭球面的空间点定位将传统意义上由曲面到平面的点投影定位方式推广到由曲面到曲面点投影定位方式，为了区别于传统意义上的地图投影，在此将曲面到曲面的投影方式称之为曲面投影。曲面投影与传统意义上的地图投影有着本质的区别，传统地图投影是指椭球面上三维曲线坐标(B，L，H)到二维平面xOy的拓扑转换，这主要是由传统的地图载体采用平面纸张及平面测量技术所决定的。而曲面投影是指在保持其空间基本特征基础上曲面本身的转换，即选择从实际椭球体地理空间(B，L，H)沿法线方向向二维曲面(B，L)投影作为空间数学基础，由(B，L)二维场所决定的椭球面几何系统作为度量空间［3，6］。

2.基于椭球面空间实体的描述

矢量地图的基本图形是点和线，在基于大地坐标的椭球面上，可将点描述为P(B，L，H)，其中，(B，L)是P(B，L，H)沿法线方向在椭球面上投影点的位置表示;直线段P1P2则由两端点P1(B1，L1， H1)、P2(B2，L2，H2)来描述，其沿法线方向在椭球面上的投影位置可由点P1'(B1，L1)到P2'(B2，L2)两投影点间的大地线段表示。

三、椭球面电子地图

计算机屏幕上可以用缩放、平移或旋转等方式显示任意形状的空间曲线和空间曲面。因此，椭球面数字地图理想的显示技术就是在计算机中设计一个椭球面，将数字地图显示在上面，从而生成一个椭球面的电子地图，如图1所示。

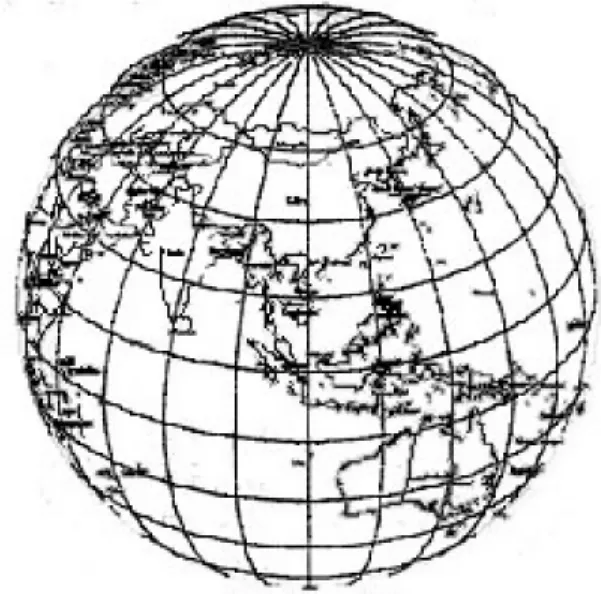
图1 椭球面电子地图示意图

椭球面电子地图的核心思想是:把计算机屏幕想象成一个无限大的平面上的一个窗口，在计算机屏幕内有一个很大的椭球体，该椭球体严格按照地球参考椭球体的大小和形状制作，可以按1∶1的比例在椭球面上绘制地图，然后用缩放、旋转等方式观看地图。

椭球面数字地图和平面数字地图虽然都是数字地图，但前者是旋转椭球面上的图形，而后者是平面上的图形。二者在空间数据的表达、地图功能的实现等方面均有着根本的不同;在空间认知方面，前者只能以电子地图的方式可视化，不能直接输出为纸质地图，而后者既可以输出为电子地图，也可以输出为纸质地图;在量测分析方面，前者用大地坐标进行运算，而后者用平面坐标进行运算，两者使用的数学模型完全不同，因此研究基于椭球面表达地表对象是一个全新的课题。

椭球面上地表对象的绘制、显示和分析都是在三维空间进行的，与平面地图有很大的差别，所以，应从以下4个方面研究基于大地坐标的椭球面电子地图。

1.椭球面电子地图的图形绘制

描述参考椭球面上点位置的方式有大地坐标和空间直角坐标两种，前者较适合用在椭球面上定位和计算，而后者较适合用在三维空间定位和计算。由于计算机绘图通常只提供三维绘图空间而不提供球面绘图空间，所以绘制椭球面上的地图图形时，必须将大地坐标转换成相应的空间直角坐标。针对计算机环境下视图与度量可以分离的特点，椭球面电子地图用大地坐标描述地理实体的位置，用空间直角坐标描绘地理实体的图形，即视图空间采用三维直角坐标系统，度量空间仍为大地坐标系统。地图显示时将大地坐标影射到空间直角坐标，地图分析时则将空间直角坐标影射到大地坐标，这样既确保了三维可视化的实现，又保证了空间度量的准确性［7］。

椭球面电子地图是矢量地图，绘制椭球面电子地图主要是研究如何绘制椭球面上的地图图形。地图图形以线段为基本图形，平面地图图形主要是以直线段为基本图形;而椭球面地图图形则是以大地线为基本图形，椭球面上的地图图形是由一系列长短不同的大地线连接构成。因此研究大地线的绘制方法是研究椭球面电子地图绘制的基本问题。

大地线是椭球面上两点的最短连线，它是一条函数方程比较复杂的空间曲线。借鉴平面曲线的绘制方法，可采用曲线光滑技术绘制大地线，即用一系列空间直线段逼近大地线，当大地线的长度小于某个阙值时可近似为直线段，超过某个阙值时则需要通过内插点位方式以保证其曲率和长度。因此，绘制大地线的核心问题首先是根据两点的大地坐标确定其大地线的函数，然后计算出该大地线上各加密点的大地坐标，最后将大地线上各点的大地坐标转换为空间直角坐标。

为了更加逼真地显示椭球面的曲面特性，以及便于视图时进行定位思维，绘制椭球面电子地图时需绘制出一个用经纬网格表示的椭球面。椭球面电子地图的空间分辨率决定经纬网格的大小，以及用空间直线段逼近大地线的最大长度。具体绘图时，按照地图的分辨率建立椭球面电子地图绘图模板，该模板由大小不同的经纬网格线构成。

平面地图的绘图空间是绘制平面直线段的平面绘图空间，椭球面地图的绘图空间则是绘制大地线的椭球面绘图空间。所以，研究椭球面电子地图的绘制实际上就是在计算机中研制一个椭球面绘图空间。

椭球面电子地图具有与平面电子地图类似的编辑功能，但因为椭球面电子地图上所编辑的图形是特殊的三维空间曲线，所以其数学模型或算法与平面地图的编辑功能将会有很大的不同。

总之，在椭球面上表达地表对象的核心问题就是如何在椭球面上绘制、处理和显示地图图形。平面地图的绘图空间是绘制平面直线段的平面绘图空间，而椭球面地图的绘图空间则是绘制大地线的椭球面绘图空间。研究椭球面电子地图的绘制、处理和显示等问题实际上就是在计算机中研制一个椭球面绘图空间。

2.椭球面电子地图的显示输出

椭球面电子地图虽然也是三维图形，但它是曲面上的图形，是球面上的“二维”地图，与普通的三维立体图形有所不同，所以其视图方法与普通三维视图不同。椭球面电子地图主要研究如何观看椭球面上的地图图形。

椭球面电子地图的视图方式类似于平面电子地图，但其缩放和平移的实现与普通电子地图有着根本的区别，椭球面电子地图的“缩放”是对椭球体的拉近放远，“平移”则是围绕椭球体中心旋转椭球面。无论“缩放”还是“平移”，椭球体的中心总是位于过屏幕中心且垂直于屏幕平面的直线上，它与屏幕的距离取决于“缩放”的倍数，椭球体轴线的旋转角则取决于“平移”的大小。

椭球面电子地图虽不能直接输出为纸质地图，但可以根据需要设计专门的地图投影计算出(x，y)。所以，以(B，L)为基础的椭球面电子地图并不排除地图投影的使用，当从数字地图输出纸质地图时仍要使用它们［8］。

3.椭球面电子地图的量算分析

基于大地坐标椭球面电子地图的量算分析都是在地球椭球面上进行的，应主要研究如何在椭球面上进行可视化的量算分析。另外，这些量算分析结果必然是参考椭球面上的，而由于参考椭球面与地球自然表面之间有一定的距离，所以由地理坐标计算的距离、角度和面积与地球自然表面上的实测值有一定的差异。在小区域的GIS中，基于地理坐标的空间分析，其大部分结果最终是要转换到地球自然表面上的。转换的方法和模型将直接影响量测分析的精度，这是椭球面电子地图必须要研究的问题。

4.椭球面电子地图与平面电子地图的转换

现行的数字/电子地图大都是基于地图投影建立的平面电子地图。要把这些平面电子地图转换为椭球面电子地图，一方面需要把平面坐标转换成大地坐标;另一方面需要重绘地图图形。另外，为了便于某些工程使用，还需要把椭球面电子地图转换成平面电子地图。总之，两种地图的转换模式也是椭球面电子地图必须要研究的问题。

四、研究椭球面电子地图的意义

基于椭球面表达地表对象，建立以参考椭球面为载体的椭球面电子地图是一个全新的概念，是最适合地理空间特征的空间数据可视化方式，符合人们将地球表面看成球面的思维和认知习惯，更容易被接受和理解，是对现有数字地图表达方式的一种改革。对于椭球面电子地图的研究将有力地拓展电子地图与数字地图的分析功能与应用范围。

将GIS的地理空间真正统一于地球科学的地理空间是GIS正确发展的迫切需要，方裕、胡鹏等学者也曾多次指出了这一点。以椭球面为定位基准建立的大地坐标系是统一的，能准确描述地球上任意点的位置，并能动态适应历史的、现代的、越来越精密的各种参考椭球体，正成为许多大区域、小比例尺的数字或电子地图以及GIS的参考框架［3，6，8］。

椭球面电子地图不以地图投影建立的平面直角坐标系统为地理基础，直接以(B，L)定义物体的空间位置，即采用(B，L，H)描述地理实体集合特征点，这样对于空间信息的处理和使用会更方便、更精确。椭球面电子地图以较大区域甚至整个地球作为对象，它能实现地理空间信息在时间域和空间域上的整体性，且能避免地图投影带来的诸多问题。所以，椭球面电子地图可作为大型GIS和数字地球最适宜的地理信息可视化方式。对于这一点可从下述几方面理解［8］:

1)只要采用的地球椭球体是统一的，则对于采用该椭球体的任何区域、任何规模的数字地图而言，由于具有真正统一的坐标系，即可以实现数据的真正共享和互操作，同时也使得建立数字地球成为可能。

2)由于不再使用地图投影，因而避免了由其带来的变形和失真。据此计算的空间关系如面积、距离、方向等都是精确的，这对于以数字化地图为地理基础的G1S来说是不可能办到的。因投影引起的变形以及变形量的不确定性，对GIS的数据处理和空间分析来说是最为忌讳的，它使得空间分析模型的“可靠性”在不同位置发生变化，难以把握，从而使GIS作用受到影响。

3)无论任何规模的GIS中，空间信息都应当是连续的，这样才能保证对任意范围、任意位置上的分析处理是可能的，分析的过程是一致的(无附加处理)。目前的GIS软件系统和算法模型尚无法办到，在其大区域应用时，空间物体的记录随着投影带的不同而采用了不同的坐标系，并且它们无法归化到一个统一的坐标系中。此外，如前所述，跨投影带的分析即使是可能的，也将是极为繁琐的。

4)由于不采用投影和分带，省去了多要素叠加分析中可能带来的投影变换问题，在地球表面上，任何两幅相邻的地图都可进行无缝拼接。由于省去了图幅与比例尺的概念，使得信息处理可以在任何范围进行，以相同的精度运算，也免去了为适应不同层次和领域的应用要求，而在同一区域重复建立不同比例尺GIS的这种费工费时、重复繁重的工作。

5)随着卫星测量技术的广泛应用，尤其是动态GPS技术在地图测绘和施工放样以及导航定位等工作中的广泛使用，地心大地坐标系正成为未来主要的坐标系统，也为大地坐标系成为数字地图主要的空间参考和框架创造了条件。

6)使得一些分析处理更为直截了当，如空间物体间的实地直线(最短)距离，也就是大圆航线的计算。在大部分地图上，这种计算很麻烦甚至很困难，但直接利用二点的地理坐标(B，L)就要简单得多。

数字地球的显示、分析与应用离不开地图形式，而且互联网上的信息也会越来愈多地出现以地图形式表达的空间信息［9］。椭球面电子地图是最适合数字地球要求的地图表现形式，深入研究椭球面电子地图对于数字地球的地图可视化、多维表示与动态显示具有非常重要的作用。

［1］ 王卉.无缝GIS相关理论与技术的研究［D］.郑州:信息工程大学，2004.

［2］ 冯琰，施一民.基于区域性椭球面数字地面模型的研究［J］.同济大学学报:自然科学版，2003，31(8): 964-967.

［3］ 胡鹏，吴艳兰，杨传勇，等.大型GIS与数字地球的空间数学基础研究［J］.武汉大学学报:信息科学版，2001，26(4):296-301.

［4］ 孙敏，赵学胜，赵仁亮.Global GIS及其关键技术［J］.武汉大学学报:信息科学版，2008，33(1):41-45.

［5］ 杨启和.地图投影变换原理与方法［M］.北京:解放军出版社，1989.

［6］ 任留成，杨晓梅，赵忠明.空间墨卡托投影研究［J］.测绘学报，2003，32(1):78-81.

［7］ 冯琰，施一民.基于区域性椭球面的三维GIS可视化模型［J］.同济大学学报:自然科学版，2004，32(9): 1192-1196.

［8］ 郭仁忠.空间信息处理中几个问题的再认识［J］.武测科技，1992(1):36-40.

［9］ 廖克.现代地图学的最新进展与新世纪的展望［J］.测绘科学，2004，29(1):5-9.

Research on Method of Expressing Earth Object in Large Scale Based on Ellipsoid Surface

YANG Yongchong，JING Xia

0494-0911(2011)12-0022-04

P208

B

2010-11-24

地理空间信息工程国家测绘局重点实验室开放课题(200819)

杨永崇(1966—)，男，甘肃皋兰人，博士，教授，主要从事数字地图与GIS应用研究工作。