GNSS/SINS组合进行惯性重力测量误差分析*
柴 华 王 勇 王虎彪 梁星辉
(1)中国科学院测量与地球物理研究所动力大地测量学重点实验室,武汉 430077 2)中国科学院研究生院,北京100049)
GNSS/SINS组合进行惯性重力测量误差分析*
柴 华1,2)王 勇1)王虎彪1)梁星辉1,2)
(1)中国科学院测量与地球物理研究所动力大地测量学重点实验室,武汉 430077 2)中国科学院研究生院,北京100049)
针对INS技术及GNSS数据处理技术,分析中国实现惯性重力测量的可能性。分析结果表明,目前中国GNSS观测与数据处理技术用于惯性重力测量已不存在技术上的困难,而国产惯性测量系统的性能指标要达到1× 10-5ms-2的重力观测精度虽有一定的困难,但随着惯性测量系统技术的进步,利用国内研制的捷联式惯导与GNSS联合进行惯性重力测量已成为可能。
惯性重力测量;捷联式惯导;GNSS;传感器精度;误差分析
1 引言
在运动载体上测量重力加速度,除了利用弹簧系统外,还可以利用加速度计进行测量。例如卫星重力测量即利用了星载加速度计实现对微重力变化的观测;俄罗斯的GT-1A航空重力仪基于加速度计原理实现了航空重力标量的测量。内置三轴加速度计的捷联式惯性测量系统(SINS)同样能够用于测量重力加速度。加速计观测值是比力,不仅包含载体运动加速度信息,同时也包含地球重力场的影响。根据广义相对论原理,仅依靠加速度计无法将比力中的重力加速度与载体的加速度区分开。若将载体运动加速度通过全球导航卫星系统(GNSS)来确定,则可将载体运动加速度从比力观测中扣除,获得运动轨迹上的重力信息。这种基于捷联式惯性导航系统(SINS)和GNSS的重力测量技术称为GNSS/SINS惯性重力测量,它能实现动态重力矢量观测(含扰动重力与垂线偏差),能较好地兼顾测量效率与分辨率。
由于惯性重力测量对惯性仪器精度的要求较为严格,及对载体速度、加速度获取的精度要求较高,硬件发展水平未能有效满足该技术的需求,直到20世纪90年代后期才有学者进行了真正意义上的基于捷联式惯导与全球卫星导航系统的航空重力测量实验[1-3]。
由于受到惯性仪器性能的限制,国内对惯性重力测量技术的研究尚处在理论探讨与前期的方法研究上,进展较缓慢。但是随着近年来国产高精度激光陀螺仪(RLG)的逐渐成熟,加速度传感器精度的提高,以及GNSS系统中精密单点定位、动态载波相位定位方法的完善,使将GNSS/SINS的组合用于惯性重力测量成为可能。本文将从惯性重力矢量测量基本原理出发,对GNSS/SINS用于惯性重力测量的各类误差进行分析,从理论上研究若要实现1× 10-5ms-2的惯性重力测量精度,SINS中各传感器及GNSS观测应达到的精度量级,并考察利用国产惯性设备进行惯性重力测量的可行性。
2 惯性重力矢量测量基本原理
GNSS/SINS组合进行惯性重力测量的基本原理,记为[4,5]:
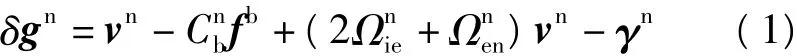
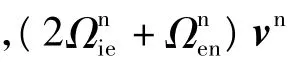
对式(1)求微分,得:
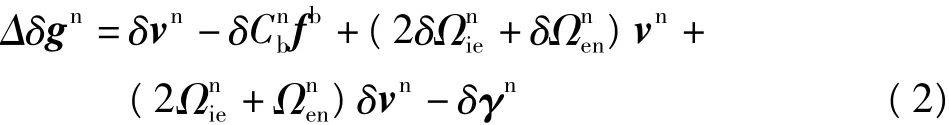
考虑向量与反对称矩阵的运算规则,式(2)等号右边第二项与第四项可写为:
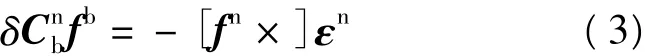
与
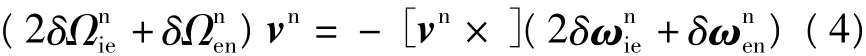
于是式(2)可写为:

式(5)即为惯性重力测量的误差方程。惯性重力测量受多种误差因素的共同影响,包括载体的动态加速度误差δvn、失准误差εn、比力观测误差δfb、测速误差δvn与位置误差δr。
3 惯性重力测量误差分析
根据惯性重力矢量测量基本原理,惯性重力矢量测量按误差来源可划分为由SINS观测引入的误差和由GNSS观测引入的误差。前者包括失准误差εn和比力观测误差δfb,后者包含载体的动态加速度误差δvn、测速误差δvn与位置误差δr。
下面对若实现1×10-5ms-2的重力测量精度,SINS中各传感器及GNSS观测应达到的精度量级展开分析。
3.1 由捷联式惯导SINS引入的误差
当地水平坐标系比力观测误差受失准角εn与载体坐标系下的比力观测误差δfb的共同影响,即
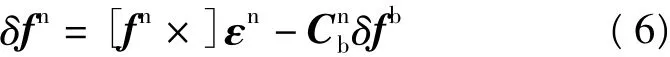
3.1.1 由SINS姿态误差引入的比力观测误差
式(6)右边第一项为:
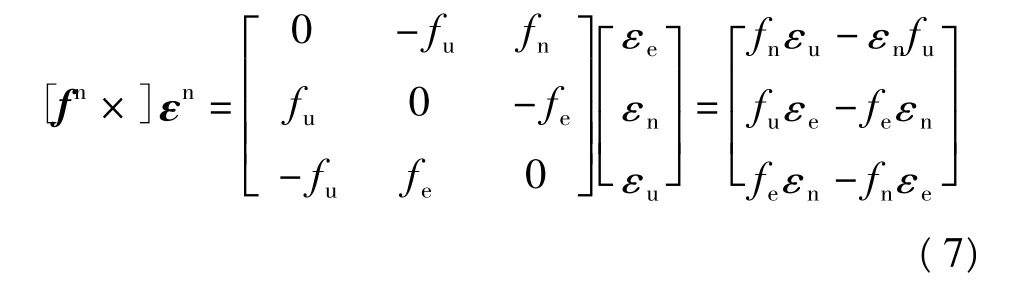
主要由失准引起。
加速度计感应到的比力f包括载体运动加速度、地球重力加速度、科里奥利加速度、离心加速度等4部分。
1)载体运动加速度
为简化问题,我们只考虑单轴的情况,假设载体的运动只存在北向加速度而其他轴向加速度为零,要实现东方向1×10-5ms-2的重力测量精度,即:
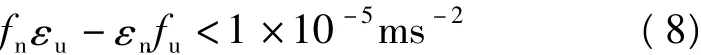
通过式(8)可以计算出在不同的水平加速度环境下,对失准角εu的要求(表1)。

表1 实现东向1×10-5ms-2的重力测量精度对失准角的要求Tab.1 Requirement of misalignment εufor 1×10-5ms-2 gravimetry accuracy eastward
从表1中可以看出,载体动态加速度的大小与对失准角的要求有直接联系。载体的动态加速度越大,达到相同的测量精度就要求失准角越小,即姿态观测的精度要求就越严格。姿态观测是由陀螺实现的,而陀螺仪本身的漂移是难以避免的,因此在惯性重力中需要尽量减小载体加速度,提高比力观测精度。通常惯性重力测量采用近匀速直线运动,此时运动加速度较小,这意味这对姿态精度的要求也相对宽松。
2)地球重力加速度
地球重力场垂向分量大约为fu=9.80 ms-2,垂线偏差在东方向和北方向上的量级在±(2~20″)范围内[6],对应于±(0.00 01~0.00 1)ms-2范围。其量级较小可将其忽略,有fn=0,fe=0。此时只考虑垂向分量fu=9.80 ms-2,式(7)简化为:
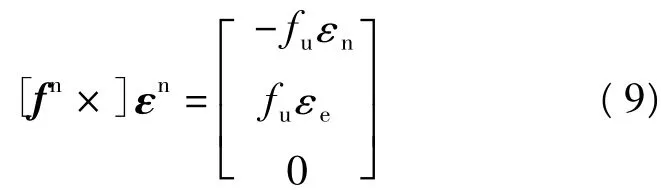
从式(9)可直观地看出,由于重力加速度的水平分量较小,失准角误差对垂向比力测量几乎没有影响;水平比力测量误差主要由垂向重力加速度耦合进水平方向引起,要实现东向1×10-5ms-2的重力测量精度,即εnfu<1×10-5ms-2,北向失准角应满足:
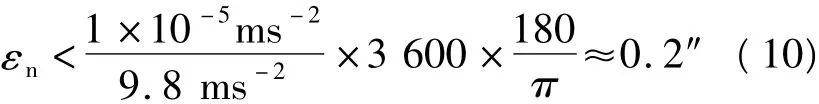
北向的情况与东向相同。
3)科里奥利加速度
科里奥利力的计算公式为:
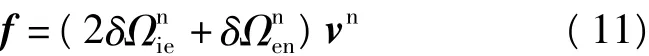
载体的运动速度越快,作用在载体上的科里奥利加速度就越大。通过式(11)可以计算出,在北纬30°的地区,一个以10 m/s的速度运动载体向东运动引起的加速度小于0.000 7 m/s2;一个以100 m/s的速度运动载体引起的加速度小于0.007 4 m/s2,这个量级的加速度在分析由失准误差引起的比力测量误差分析时可以忽略。
经分析可知,在惯性重力测量中应尽量保持载体的匀速运动状态,可以减小载体姿态的失准误差对比力观测的影响;在匀速运动的情况下,姿态误差引起的水平比力测量误差主要是由耦合进水平方向的重力引起,并严重降低垂线偏差的测量精度。
载体的失准误差主要由陀螺的漂移引起,若要求实现1×10-5ms-2的重力测量精度,陀螺的漂移应满足[4]:


表2为捷联惯导中不同精度的陀螺对垂线偏差观测的影响。

表2 陀螺漂移对垂线偏差测量精度的影响Tab.2 Influence of gyro drift on vertical deflection
当前装备有漂移为0.002°/h~0.005°/h小型激光陀螺的惯性测量系统,要实现1×10-5ms-2的垂线偏差测量精度,陀螺精度还需要提高一个数量级。
3.1.2 由SINS加速度计误差引入的比力观测误差

式中第一项b为加速度计的零偏,包括常值零偏和随机零偏,常值零偏通常可在实验室中进行标定后补偿。随机零偏包括开机后的随机零偏与环境变化引起的零偏,前者可以通过现场标定的方式补偿,后者一般建议通过精确的环境温度控制来减小影响[5]。若要达到1 ×10-5ms-2的比力测量精度要求则要求未得到补偿的零偏及其变化,即零偏稳定性小于1×10-5ms-2。Sffb为比例因子相关项,Sf为加速度计比例因子的常数对角矩阵,通常量级为1~10 ppm[4]。对惯性重力测量而言,因受重力加速度影响比例因子误差对垂向比力观测的影响最为强烈,而在水平方向上比力观测的影响较小。在载体做水平匀速运动的情况下,比例因子误差引起的比力误差近似为常值,故可将其视为常值零偏,此时比例因子的稳定性将是影响测量精度的主要原因。若要在垂向达到1×10-5ms-2的重力测量精度,其比例因子稳定性应小于1 ppm。Nffb是由加速度计的安装误差矩阵引起的比力误差,Nf矩阵描述了从加速度计载体坐标系到IMU载体坐标系间的失准,它是一个反对称矩阵[7],可以通过实验室标定的方法来定量地获取。其对比力观测的影响为[5]:
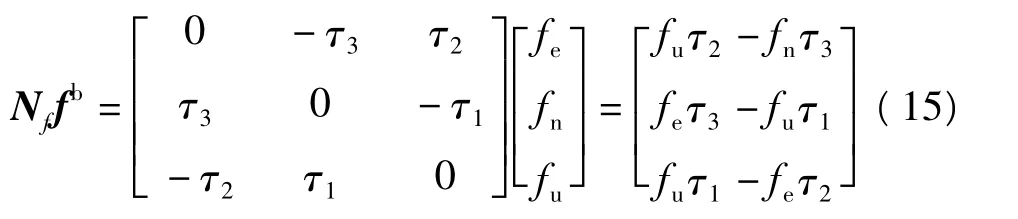
在载体做匀速运动的情况下,fe与fn为小量,于是有:

分析式(16)可知,加速度计安装误差的存在将使地球重力垂向分量耦合进水平方向,使水平方向的比力呈现较大的误差,而由于fe与fn为小量,垂直方向的比力观测受影响较轻微,若要使水平方向观测的比力精度优于1×10-5ms-2,则加速度计的安装误差应满足:

速度计的安装误差τ通常可通过实验室标定后进行补偿,且在载体匀速直线运动状态下对水平比力误差的影响近似为常值,因此在惯性重力测量中亦可将其可视为常值零偏。
图1为某型号高精度石英挠性加速度计的静态观测数据。从图中可以看出加速度计的观测数据中含有大量高频噪声,其最大的影响量级为1 000× 10-5ms-2,因此必须限制其影响。通常是根据载体的运动速度与重力测量要求的分辨率设计低通滤波器,将高频噪声的影响限制在10-5ms-2量级[1,2]。

图1 含有高频噪声的石英挠性加速度计观测时间序列(5s,200 Hz)Fig.1 Time sequence of observation with flexible quartz accelerometer(5s,200 Hz)of high frequency noise
表3为比力观测对加速度计的要求。值得注意的是,比力观测误差受各类误差的共同影响,若要实现1×10-5ms-2重力观测,要求各影响因素之和必须小于其最大影响。

表3 达到1×10-5ms-2的比力测量精度对加速度计的需求Tab.3 Requirement of the accelerometer for 1×10-5ms-2 level specific force observation
表4为当前高精度石英挠性加速度计精度情况。显然以当前加速度计硬件的精度,达到惯性测量实用的水平并实现1×10-5ms-2的惯性重力测量精度仍有一定差距。

表4 当前高精度石英挠性加速度计的精度Tab.4 Accuracy of present high precision quartz flexible accelerometer
3.2 由GNSS观测引入的误差
由GNSS观测引入的误差包括载体的动态加速度误差、测速误差和定位误差。
1)载体的动态加速度误差δ v·n
重力测量中,载体的动态加速度误差δ v·n通过比力方程直接与测量的扰动重力发生联系,若要达到1×10-5ms-2的重力测量精度,δ v·n需满足
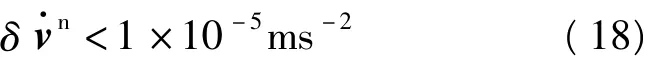
通常载体的动态加速度是对DGPS的位置结果做二次差分得到的,由于在差分过程中会产生大量的高频噪声,因此需要在估计扰动重力时结合动态测量分辨率的要求设计低通滤波器消除其影响[8,9]。
研究表明,差分方法在GNSS加速度的获取中具有优势,Hwang C等[10]的研究结果说明,差分可以有效减小位置观测中的长波误差对速度、加速度获取的影响。
2)测速误差δvn
测速误差对惯性重力测量的影响主要体现在理论科里奥利加速度的计算误差上。
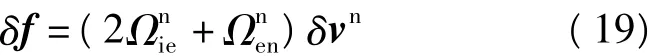
将上式展开写为:

式中,
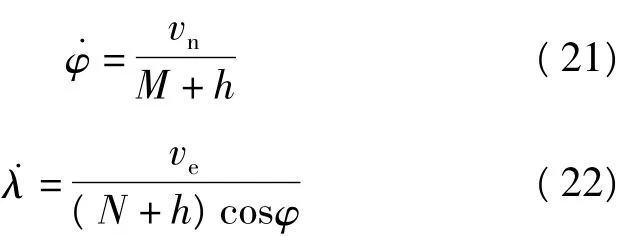
可见由速度误差引起的比力测量误差与载体所在的纬度和运动速度有直接关系,为简化问题,这里我们只选择北方向的比力测量误差进行考察,并假设载体向东运动,若要求达到小于1×10-5ms-2的北向比力测量误差,对东向测速误差的要求可利用式(20)与(22)计算。将在不同纬度的地区在不同速度的情况下对于测速精度的要求列于表5。
从表5中可以看出,纬度越高对测速精度的要求就越高,载体运动速度越快对测速的要求也越高。其他轴向的比力误差与存在北向速度的情况亦可类似分析。若采用载波相位差分观测在整周模糊度正确固定的情况下,当前GNSS系统测速精度可以达到3~5 cm/s,能够满足1×10-5ms-2的比力测量的需求。

表5 不同纬度的地区在不同速度的情况对测速精度的要求Tab.5 Velocity accuracy requirement for different latitude and velocity
测速误差的影响还间接地体现在式(5)中的[vn×](2δ+δ)项内,因在角速率中:
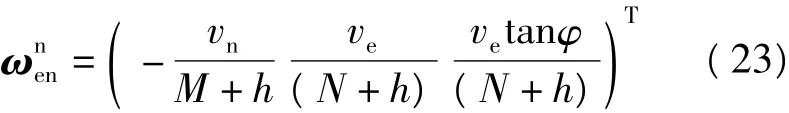

左乘反对称矩阵-[vn×],

同样选择北向的比力测量误差进行考察并假设载体向东运动,可利用式(25)计算出北向的比力误差为

由式(26)可知,载体的运动速度越大,速度观测误差越大,纬度越高,则比力测量误差越大。在纬度为60°的地区,一个以100 m/s运动的载体,对于当前测速精度达到5 cm/s的GNSS系统观测而言,引起的比力误差仅为0.14×10-5ms-2;或当测速误差大于37 cm/s时,引起的比力测量误差为1×10-5ms-2。
3)位置误差δr
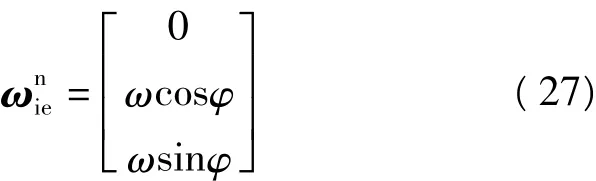
对式(23)与(27)求微分,分别得到:
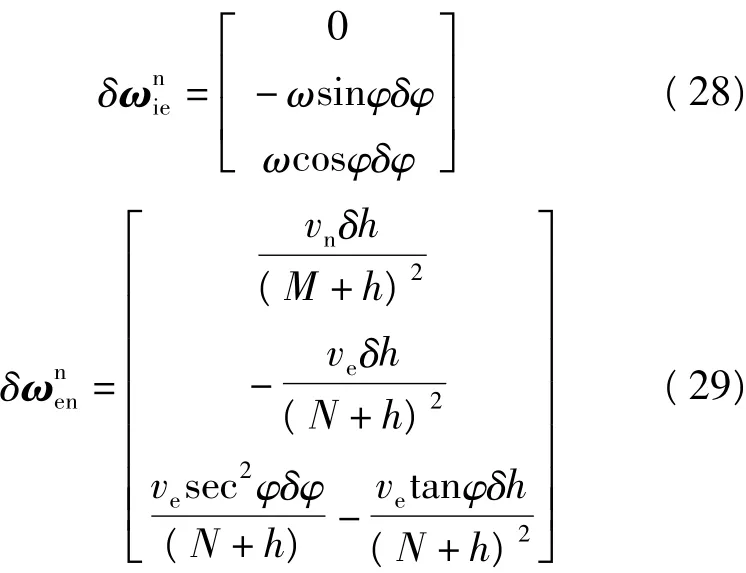
地球自转角速度ω=7.292 115×10-5rad/s,若纬向的定位误差为5 m,则:
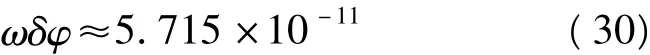
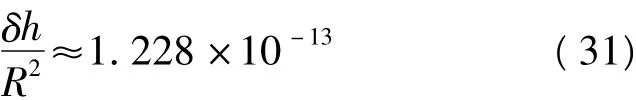
由位置误差引起的正常重力计算误差可以通过水平和垂直两个方向的分量来描述。垂直方向影响较大,约为0.308 6h。即大约高程上出现3.2 m的误差,对于垂向比力测量的影响即达到1×10-5ms-2。当前从差分动态GNSS的位置测量精度在整周模糊度正确固定的情况下为3~5 cm,若用户站与基准站相隔较远,会导致定位误差下降到分米级,但只要高程测量误差上小于3 m,即可保证其对扰动重力的影响小于1×10-5ms-2。
水平方向的影响可用公式 0.813sin2φ 10-5ms-2/km来描述[12],此时正常重力计算误差是纬度的函数,在北纬30°地区且定位误差达1 400 m的情况下,其影响约为1×10-5ms-2,相对于cm级别的定位误差,由水平位置误差引起的正常重力计算误差可以忽略。
分析表明,在相对理想的观测条件下,GNSS观测与数据处理技术用于惯性重力测量已不存在技术上的困难,但在实际观测中,如在航空测量应用中,易受航路气流与气象条件的限制;或在多云或下雨的环境中产生的扰动,易使GPS的观测受到影响进而影响重力信号的提取[10],需在测量中注意。
4 讨论
结合当前国内惯性器件与GNSS技术的发展水平,表6给出了用于惯性重力测量的国产惯性测量系统的精度要求。

表6 国产捷联式惯性重力测量系统精度要求Fig.6 Precision requirement for domestic strapdown inertial gravimetry system
通过分析可知,若要达到1×10-5ms-2的重力测量精度,由GNSS确定的载体动态加速度误差应小于1×10-5ms-2,在北纬60°的地区测速误差应不大于6.5cm/s,垂向位置误差小于3.2m。这样的精度对于GNSS观测与数据处理而言在技术上是可以实现的。
对于SINS系统,一方面由陀螺漂移导致的失准误差是由姿态误差引入的最主要误差源,它对垂线偏差测量精度有较大的影响;另一方面,只有加速度计的各类误差的共同影响小于1×10-5ms-2才有可能实现1×10-5ms-2的动态重力测量精度。虽然近年来国内惯性器件精度取得了长足的进步,但与达到1×10-5ms-2的重力测量精度的硬件要求仍有距离。从国外惯性航空重力测量的结果来看,例如Jekeli在航空重力矢量测量的研究中利用的陀螺与零偏为量级的加速度计获得了垂向(3~4)×10-5ms-2、水平方向(6~8)×10-5ms-2的重力测量精度。其实现方法是将GNSS的观测与SINS的观测进行卡尔曼滤波融合,将它们对比力测量的影响估计出来,进而用于修正比力观测,提高惯性重力测量的精度。当国产惯性测量系统内各硬件的精度能够达到表6中所列的精度的指标时,就完全有可能以达到或超越与国外实验的精度进行动态惯性重力测量。
随着国产惯性器件制造工艺的进步与GNSS数据处理技术的完善,利用国内研制的捷联式惯导与GNSS联合进行惯性重力测量的条件正逐渐走向成熟。
1 Bruton A M.Improving the accuracy and resolution of SINS/ DGPS airborne gravimetry[D].University of Calgary, 2000.
2 Kwon J H.Airborne vector gravimetry using GPS/INS[D].The Ohio State University,2000.
3 Senobari M S.New results in airborne vector gravimetry using strapdown INS/DGPS[J].Journal of Geodesy,2010,84(5):277-291.
4 董绪荣,等.GPS/INS组合导航定位及其应用[M].长沙:国防科技大学出版社,1998.(Dong Xurong,et al.GPS/INS integrated navigation and positioning with its applications.[M].Changsha:National Defense Technology Press,1998)
5 张开东.基于SINS/DGPS的航空重力测量方法研究[D].国防科技大学,2007.(Zhang Kaidong.Research on the methods of airborne gravimetry based on SINS/DGPS[D].National University of Defense Technology,2007)
6 丁一帆,等.现代大地测量学中的垂线偏差[J].大地测量与地球动力学,2006,(2):115-119.(Ding Yifan,et al.Deflection of vertical on modern geodesy[J].Journal of Geodesy and Geodynamics,2006,(2):115-119)
7 Titterton D H,at al.Strapdown inertial navigation technology(2nd edition)[M].The Institution of Electrical Engineers,2004.
8 孙中苗,等.FIR低通差分器的设计及其在航空重力测量中的应用[J].地球物理学报,2000,43(6):850-855.(Sun Zhongmiao,et al.Design of FIR low-pass differentiator and its applications in airborne gravimetry[J].Chinese Journal Geophysics,2000,43(6):850-855)
9 应俊俊,等.航空重力测量中利用GPS测定载体的速度和垂直加速度[J].大地测量与地球动力学,2009,(5):68-71.(Ying Junjun,et al.Determination of velocity and vertical acceleration in airborne gravimetry by using GPS[J].Journal of Geodesy and Geodynamics,2009,(5):68 -71)
10 Hwang C,et al.Geodetic and geophysical results from a Taiwan airborne gravity survey:Data reduction and accuracy assessment[J].J Geophys Res.,2007,112,B04407.
11 Jekeli C.Inertial navigation systems with geodetic applications[M].Berlin NewYork:Walter de Gruyter,2001.
12 Torge W.Gravimetry[M].Berlin New York:Walter De Gruyter,1989.
ERROR ANALYSIS FOR INERTIAL GRAVIMETRY BY USE OF GNSS/SINS COMBINATION
Chai Hua1,2),Wang Yong1),Wang Hubiao1)and Liang xinghui1,2)
(1)Key Laboratory of Dynamic Geodesy,Institute of Geodesy and Geophysics,CAS,Wuhan 430077 2)Graduate University of the Chinese Academy of Sciences,Beijing100049)
As focusing on present domestic INS technology and GNSS data processing technology,the feasibility for carrying out inertial gravimetry experiment with domestic inertial navigation system is discussed.The results from the analysis show that,although GNSS observation and data processing have not big issues presently,it is still hard to reach 1×10-5ms-2gravity accuracy by use of the inertial navigation system.However,with the technical progress of the domestic inertial system,the day for inertial gravimetry with domestic inertial navigation system is approaching.
inertial gravimetry;SINS;GNSS;accuracy of sensor;error analysis
1671-5942(2011)06-0073-06
2011-04-25
国家自然科学基金(41074051,40974044);中国科学院动力大地测量学重点实验室基金(L09-18);武汉大学地球空间环境与大地测量教育部重点实验室基金(10-01-05)
柴华,男,1981年生,博士生,主要从事惯性测量数据处理、GNSS/SINS重力测量方面的研究.E-mail:hchai@asch.whigg.ac.cn
P227.9
A

