研发创新SBM效率的国际比较研究——基于OECD国家和中国的实证分析

钟祖昌

（广东外语外贸大学 国际工商管理学院，广东 广州510006）

一、引言与文献综述

创新是社会发展的直接动力，自从国家创新系统理论提出以来，它已成为学者们研究不同国家或区域经济发展差异的重要工具。近年来，我国科技经济投入增长迅速，数据显示，中国研发经费支出R＆D占GDP的比重不断攀升，从2000年的0．9% 增长到2010年的1．75%，但与世界领先国家R＆D占GDP的比重平均为3%左右相比仍有较大差距。在科技经费投入快速增长的背景下，我国的创新效率是否得到提高，与发达国家的差距有多大，创新效率的差距有没有缩小的趋势？这正是本文的研究目的所在。

现有文献中以国家或地区为考察对象，对不同国家或地区间研发创新资源的投入产出效率进行测算与比较是创新效率研究中的一个重要方向（Nasi-erowski和 Arcelus，2003；Wang等，2007；Sharma和 Thomas，2008），其目的主要是通过国家或地区间的比较发现效率差异的原因，从而为低效率地区的效率改善提供借鉴。国内学者白俊红等（2009）认为中国研发创新效率仍处于较低水平但逐年提高，各主体要素及其之间的联结对创新效率均产生负向作用，这反映出中国当前区域创新系统网络建设并不理想。史修松等（2009）运用随机前沿函数分析方法，以省级区域为样本测算并分析了中国区域创新效率及其空间差异。研究表明，中国区域创新效率总体水平不高，区域差异较为明显，东部地区的创新效率要高于中西部地区。于明超（2010）指出自主研发资本存量是影响创新产出的主要决定因素，技术消化吸收对创新产出有显著的影响，而国内外技术引进则对内部研发有替代效应。罗亚非等（2010）运用超效率DEA方法对不同国家1998-2005年研发创新活动进行效率评价，指出大多数国家的研发创新主要依靠规模效率推动。

综上所述，本文采用OECD30个成员国和我国2001-2008年面板数据，运用Fried等（2002）提出的三阶段DEA方法，结合Tone（2001）提出的SBM方法的优点，剔除各国环境变量和随机冲击对创新效率的影响，客观评价各国的创新效率，并分析创新效率差距的动态演化特征，为我国未来科技政策的制定、科技投入的重点以及提高自主创新能力提供借鉴。

二、模型与变量选择

（一）SBM方法和三阶段DEA模型

本文将SBM模型与三阶段DEA方法相结合，利用修正的三阶段DEA法，考虑松弛变量对效率测度的影响，同时将外部环境和随机冲击的影响剥离，以更准确地评估各个国家的创新效率。修正的三阶段DEA方法基本步骤如下：

第一阶段：SBM模型。传统的DEA方法，如CCR和BBC模型，在评价决策单元效率时没有考虑松弛变量的影响，可能会造成效率测度的偏差。同时，在投入要素增多且考虑松弛产出的情况下，整体比较决策单元的效率将变得更加困难。我们将运用Tone（2001）所提出的投入导向可变规模报酬下SBM效率评价模型来测量第一阶段各国的创新效率。具体的SBM模型如下：

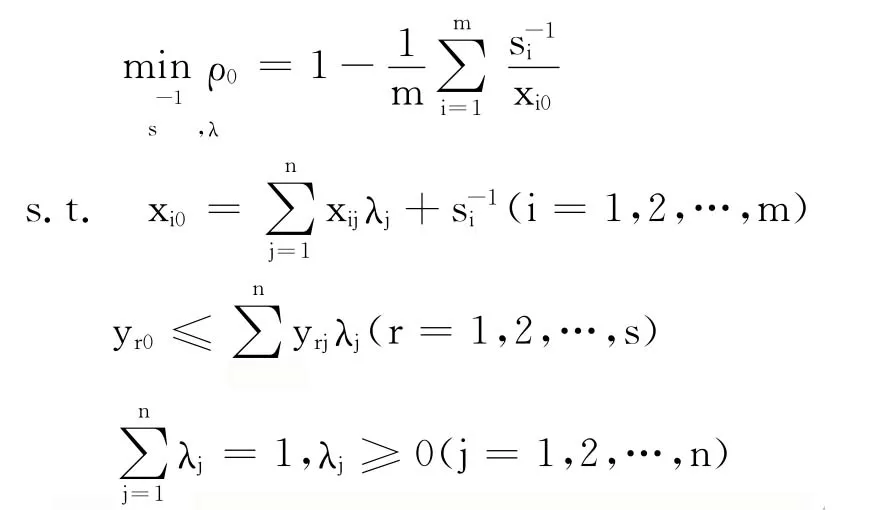
其中，ρ0为效率评价标准，m为投入要素的种类，s为产出的种类，λ＝（λ1，λ2，…，λn）′为权重向量表示第i个投入的松弛变量；x0和y0分别为决策单元自身的投入和产出向量，X和Y分别为决策单元整体的投入和产出。

从Tone（2001）的模型中可以看到，当投入和产出约束越松弛，也就是松弛投入和松弛产出越大时，企业的效率值越低，较好地将松弛投入和松弛产出的情况考虑在效率计算过程中。如果一个企业根据Tone（2001）的评价标准是有效的，即投入松弛变量为0，我们可以得到SBM模型中的效率值ρ0＝1，该性质被称为Pareto-Koopmans有效。

第二阶段：构建相似SFA分析模型。为了分离出受外部环境和随机误差因素影响的效率值，必须调整投入量，在第二阶段通过构建类似SFA模型可分别观测出环境因素、随机误差和管理无效率三个因素的影响，从而得出仅是由管理无效率造成的决策单元投入冗余。第一阶段的投入松弛变量如下：

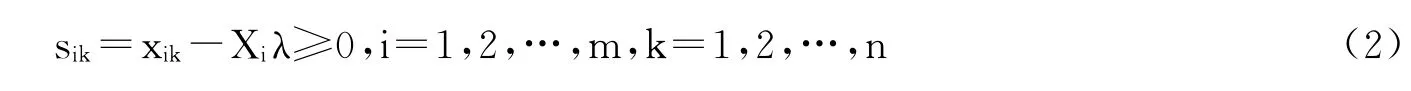
其中，sik是第一阶段第k个决策单元使用第i个投入的松弛变量（射线上的加上非射线上的），也表示第k个决策单元第i项投入实际值与最优值的差额。Xi是第i行的X，Xiλ是xik对应产出向量在投入效率子集上的最优映射。

建立松弛变量与环境解释变量的理论模型：

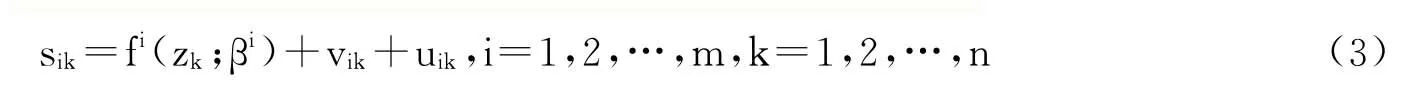
其中，zk＝（z1k，z2k，…，zpk）表示p个可观测的环境变量，βi为环境变量的待估参数向量；fi（zk；βi）表示环境变量对投入差额值sik的影响方式，一般以线性形式表示。vik+uik为混合误差项，uik表示管理无效率，并假设其服从截断正态分布，即uik～N+（u）。vik表示随机干扰项，并假定其服从零均值、同方差的正态分布，方差为。vik和uik独立不相关。特别地，令γ＝／+），γ趋近于0时，随机误差项占主导地位；γ趋近于1时，管理因素的影响占主导地位。

为进行下一步的投入调整，有必要先从SFA回归模型的混合误差项中把随机误差从管理无效率中分离出来。通过管理无效率的条件估计并借鉴Jondrow等（1982）提出的方法，得到随机误差的估计为：

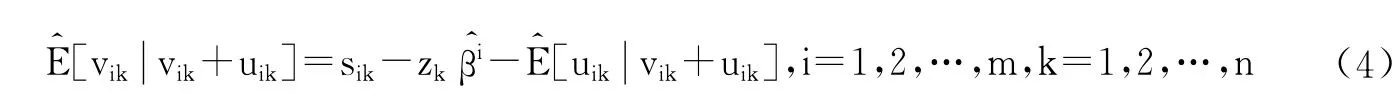
为剥离不同外部环境和随机误差的影响，本文选择对于那些处于相对有利的运营环境或相对较好的决策单元的投入进行向上调整。基于最有效率的决策单元，以其投入量为基准，对其他各决策单元投入量的调整公式如下：

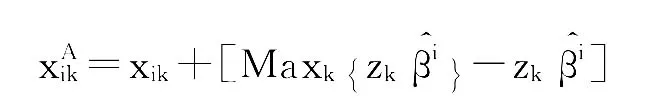
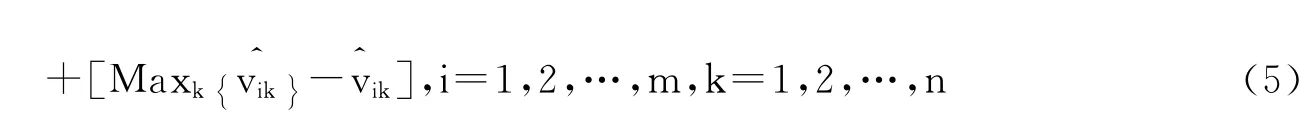
第三阶段：调整后的SBM效率值。用第二阶段调整后的决策单元投入数据代替原始投入数据，再次运用SBM模型进行效率评估。此时得到的各决策单元的效率值即为剔除环境因素和随机误差后的SBM效率。

（二）投入产出变量、环境变量选择与数据说明

1．投入产出变量选择

在众多创新投入和产出指标中，基于数据的可得性和全部决策单元数据的一致性，本文选择了2个投入指标和3个产出指标。

创新投入指标方面，资本投入和劳动投入是研究投入产出效率常用的指标，本文也使用资本和劳动投入。这里选择了各国研发资金投入和科学家工程师全时当量两个指标作为投入变量，单位分别为亿美元和万人年。

创新产出指标方面，本文选择了三方专利数量、高质量科技论文数和高技术产品工业增加值作为研发活动的三大产出指标。其中，三方专利是在欧洲专利局、日本专利局和美国专利商标局都获准的专利。高质量科技论文数是指发表在被美国科技信息所（ISI）检索的5000余种期刊上的论文数量。

由于研发投入具有一定的滞后性，本文采用研发产出前5年的投入数据均值作为研发投入（Graves，1996），即产出为i+5年数据而投入取值为i年至i+4年的5年平均值。

2．环境变量选择

环境变量应选择那些对创新效率产生影响但不在样本主观可控范围内的因素。考虑到创新活动的特点，本文选择以下几个因素作为环境变量：

（1）人均国内生产总值（RGDP）。许多文献表明，经济发展水平与创新投入和创新效率存在直接的正向关系，人均GDP能充分代表国家经济发展水平，因此，我们把人均GDP作为重要的环境变量，单位为美元。

（2）产业结构（HTI）。由于不同产业的知识基础、投资要求和创新过程存在着差异，因此区域产业结构成为影响区域创新效率的重要因素。本文以各国的高技术产业增加值占该国生产总值的比重作为该解释变量的代表，这里使用的是国际上通用的国际标准产业分类（ISIC）。

（3）政府支持（GOV）。政府是研发创新活动有效开展的重要支持机构，其通过财政科技拨款、税收优惠和政府采购等渠道对创新活动进行直接资助。本文用政府科技拨款占研发费用的比例来表示政府对创新活动的支持。

（4）对外依存度（OPEN）。一个地区的对外开放程度直接影响其创新的广度、深度和效果。开放程度高的地区能更多地接触国外的先进技术和管理方式；本文主要用进出口总额占该地区生产总值的比重来反映地区的对外依存度，并借此考察其对区域创新效率的影响。

3．样本数据来源

关于样本的数量，根据数据的可得性和完整性原则，OECD现有34个成员国，考虑到智利、爱沙尼亚、以色列和斯洛文尼亚是2010年以后才加入的，因此，在样本中予以剔除，再加上中国，总共有31个样本。

研发资金投入（GERD）、研发科学家工程师全时当量（Researchers FET）和环境变量的数据均来自OECD历年的统计数据报告（OECD Main Science and Technology Indicators），各国被授权的三方专利数量来自OECD历年的统计报告（OECD Factbook），科技论文数和高技术产业工业增加值数据来自美国科学基金会历年的报告（Science and Engineering Indicators）。以货币计量的数据均转换为2000年不变价格的美元。

三、实证结果分析

（一）第一阶段SBM效率分析

第一阶段的创新SBM效率值计算结果如表1所示，从各国的平均效率得分情况来看，最高为瑞士（0．761），其次为荷兰（0．689），最低为挪威（0．402）；中国的创新效率得分为0．554，低于OECD创新效率的平均水平，排名第17，与大部分OECD国家相比仍有较大差距。从各国创新效率的演化趋势来看，2001-2008年我国创新SBM效率值总体上呈现上升的态势，斯洛伐克和瑞典的波动幅度较大，美国呈现先上升后下降的态势，爱尔兰和挪威的创新效率则基本稳定。

鉴于第一阶段的创新效率得分没有区分各国不同的宏观经济环境和随机冲击，可能有一些国家无法控制的环境变量和随机冲击对其创新效率得分产生显著影响，因此，直接用SBM效率或其他效率进行比较都显不公平。考虑到这一点，本文将在第二阶段对主要环境变量和随机冲击的影响进行检验。

表1 2001-2008年各国创新SBM效率值

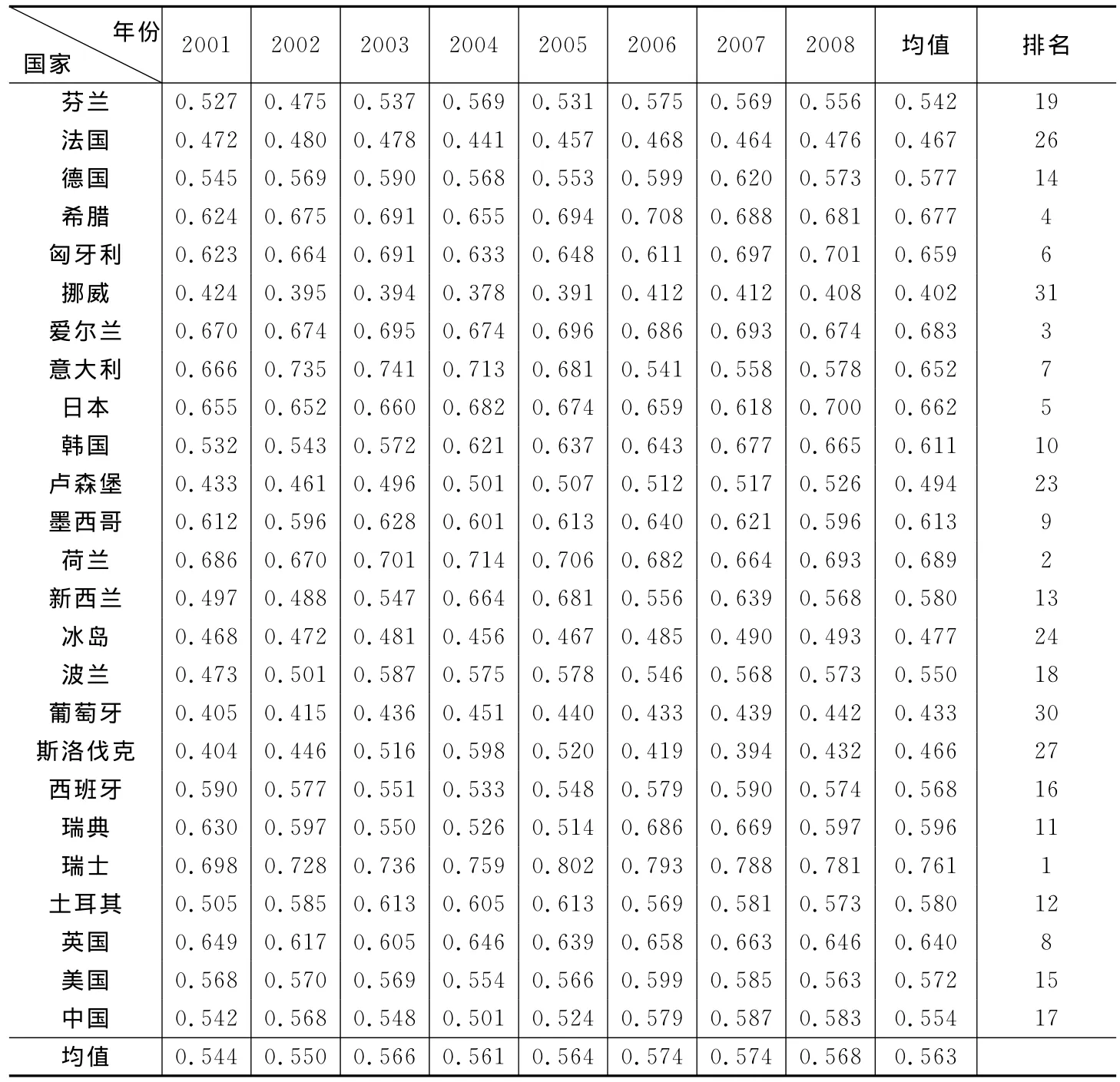
续表1 2001-2008年各国创新SBM效率值

（二）第二阶段SFA回归结果

将第一阶段得出的各国各投入变量的松弛变量作为被解释变量，将人均GDP、产业结构、政府支持和对外依存度作为解释变量，利用FRONTIER4．1软件进行SFA回归。我们以2008年为例，结果如表2所示。

由表2可知，从模型设定的可靠性检验来看，2项投入松弛变量对应的SFA模型的单边似然比检验LR统计值均大于mixedχ2分布的检验标准值，表明模型的估计结果在总体上可以接受；变差率的估计值则表明综合误差项中存在技术非效率，因此，使用SFA分析是必要的。同时，人均GDP、产业结构、政府支持力度和对外依存度等变量对两种投入松弛变量的系数均通过5%的显著性水平检验，这也表明外部环境因素对各国创新投入冗余产生了影响。

投入松弛变量是各地区可以通过改善其运营管理水平，从而达到效率前沿可能节约的投入量。因而，可以将投入松弛变量视为各地区的机会成本，解释变量与投入松弛变量正相关表明该解释变量不利于创新效率的提高；反之，二者负相关，则表明该解释变量有利于创新效率的提高。因此，从环境因素对投入松弛变量的回归系数来看，可得出如下结论：（1）地区人均GDP对创新效率两种投入要素松弛变量回归系数均为负且均通过1%的显著性检验，表明一国GDP的增加将导致创新经费投入和创新人员投入的减少。（2）政府支持力度对创新效率两种投入要素松弛变量回归系数均为正且均通过1%的显著性检验，表明政府支持力度的加大将导致资本和从业人员投入的增加。（3）产业结构对创新效率两种投入要素松弛变量回归系数均为负且均通过1%的显著性检验，说明产业结构的调整是推动一国创新效率提高的重要力量。（4）对外依存度对创新效率两种投入要素松弛变量回归系数均为负且均通过5%的显著性检验，表明一国的对外开放有利于获取发达国家的技术创新溢出效应。

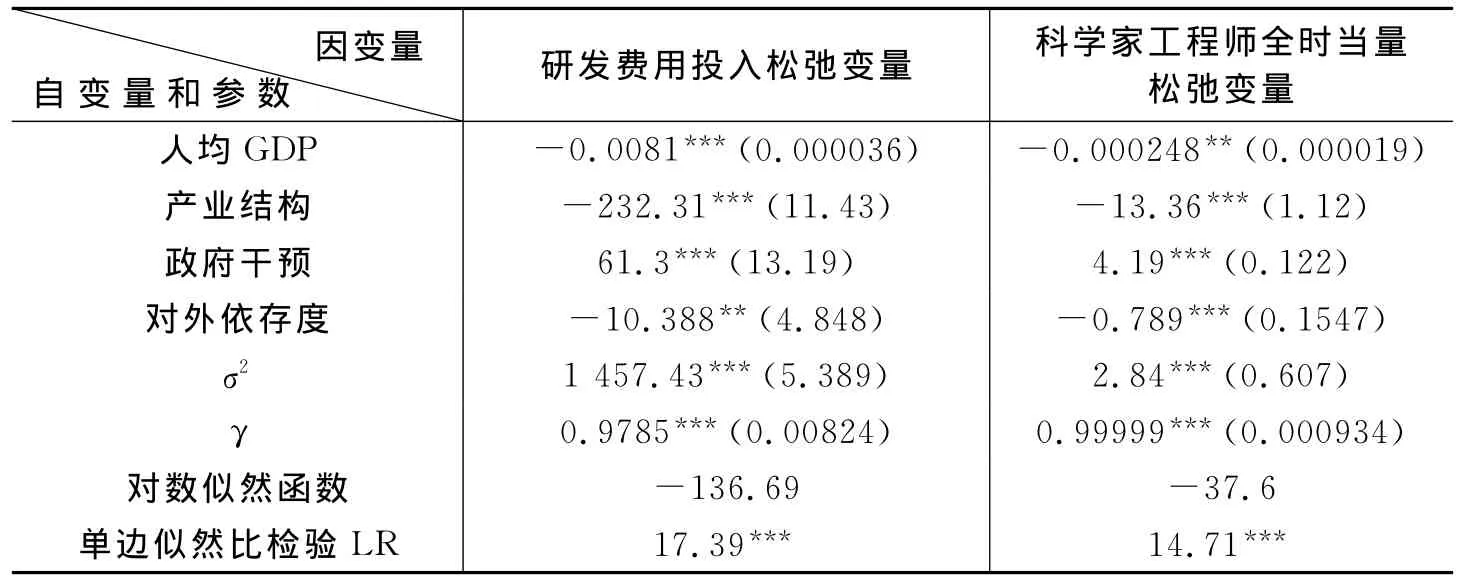
表2 第二阶段SFA估计结果（2008年）

由上述分析可知，由于各环境变量对于不同决策单元的影响有所不同，一些宏观环境或运气较好的国家具有较佳的效率表现，而一些宏观环境或运气较差的国家则具有较差的效率表现，从而导致对决策单元效率的不准确评判。因此，必须调整原投入变量，使所有的国家面对同样的外部环境和随机冲击，以准确考量真实的创新效率水平。

（三）第三阶段SBM效率

根据式（5），对投入变量重新进行调整，再次运用SBM模型，得到调整后的实际SBM效率（见表3）。

本文采用Wilcoxon符号等级检验对第一阶段与第三阶段SBM的各效率值进行显著性差异分析。结果表明，第一阶段的效率值与第三阶段的效率值存在显著差异，表明本文所选择的环境变量和随机因素确实会对各国创新SBM效率值产生影响，因此调整投入变量很有必要。

对比表1和表3可以看到，各国整体创新SBM效率指标由0．563上升到0．646，提升约14．74%。整体上来看，各国创新SBM效率指标都得到明显提升，说明各个国家的创新SBM效率比看上去要高。从各国的具体情况来看，提升幅度最低的为新西兰，提升3．43%，其次为法国（7．65%）和波兰（11．42%）；最高的为卢森堡，提升25．69%，其次为葡萄牙（23．52%）和斯洛伐克（19．29%），中国创新SBM效率指标提高了15．47%，排名第16，说明这些国家之前较低的创新效率确实部分是由较差的环境或不好的运气所致，而非它们的技术管理水平差。以上分析表明在不考虑环境因素和随机冲击的情况下，各国创新SBM效率值往往被低估。

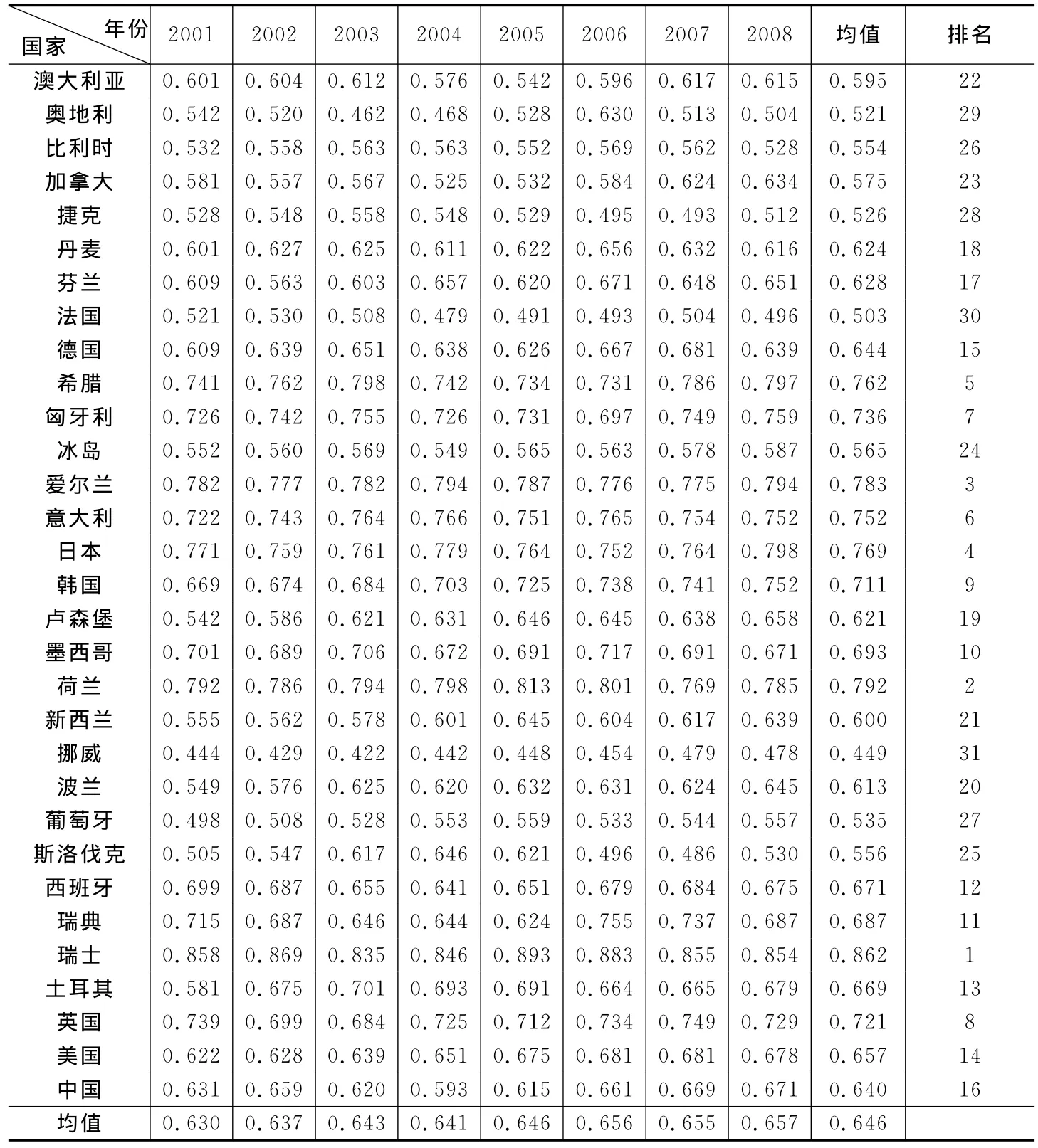
表3 调整后的各国创新SBM效率值

我们对调整前和调整后的排名进行了相关性分析，发现各国排名向量的相关系数为0．942。这说明整体上各国排名没有因环境影响和随机冲击而发生颠覆性的变化。从各国情况来看，调整前后创新效率排名前三的国家没有发生变化，依次为瑞士、荷兰和爱尔兰，法国由调整前的第26位下降到第30位，新西兰由调整前的第13位下降到第21位，西班牙和卢森堡排名上升幅度较大，分别由调整前的第16和23位上升到第12和19位。

四、各国创新总体效率与区域差异分析

第三阶段的创新效率值剔除了环境因素和随机因素的影响，更能反映各国创新的实际发展情况，以下分析将以第三阶段结果为基础，对各国创新SBM效率做进一步深入分析。

（一）各国创新SBM效率值总体分析与年度波动

从总体上来看，如表3所示，调整后OECD和中国的平均创新SBM效率为0．646，仍存在较大的无效率。从各国的具体情况来看，调整后平均创新效率值排名前三位的国家分别是瑞士（0．8616）、荷兰（0．7922）和爱尔兰（0．783），这主要得益于这些国家在创新产出方面表现较优，特别是瑞士在创新投入和创新产出两个方面均具有较大优势。排名最后的三个国家是挪威（0．4492）、法国（0．5027）和奥地利（0．5208），这些国家在创新产出方面均表现较差，导致创新效率低下。

从各年的情况来看，调整后的创新效率波动要小于调整前，最高的平均效率为2008年的0．6571，最低为2001年的0．6296。各国效率中，最高为2005年瑞士0．8932，最低为2003年挪威0．4216。这进一步说明环境变量和随机冲击对各国创新SBM效率的影响较大，将这些外生变量和随机冲击的影响熨平后，创新效率的波动和差别会明显减小。

（二）地区差异分析

我们将上面的31个国家按照地域特征分成四组——欧洲、北美洲、日、韩和中国，计算结果如表4所示，从均值来看，日、韩的创新效率值最高，达到0．74，北美洲次之，欧洲平均创新效率最低。从年度波动情况来看，日、韩出现明显的效率上升趋势，欧洲效率相对较为平稳，而中国在经历2004年低谷之后平均效率开始逐步上升，和各国差距也在逐渐缩小，这也从另一侧面反映了随着世界经济一体化进程的加快，我国通过扩大对外开放、引进国外先进技术进行消化吸收再模仿创新，最终走上自主创新道路的战略的有效性，同时也说明了国际产业转移趋势、跨国要素流动驱动使得国家间的经济活动和创新活动联系更加密切。

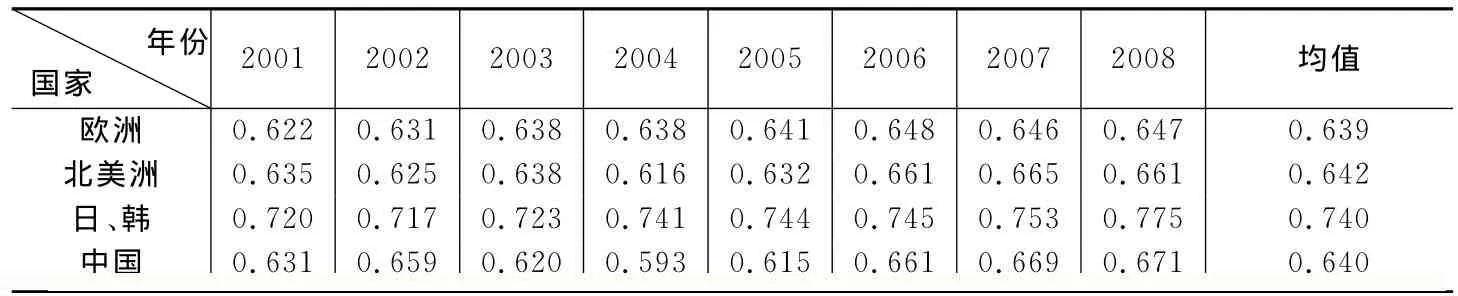
表4 OECD国家创新效率地区差异

五、结 论

本文将SBM模型与Fried等（2002）提出的三阶段DEA方法相结合，考虑松弛变量对效率测度的影响，同时控制外部环境和随机冲击的影响，实证评估了2001-2008年30个OECD国家和中国的创新效率。本文得到如下结论：

第一，经济发展水平、产业结构、贸易依存度和政府干预等环境变量对各国创新的投入松弛程度有重要影响。其中，经济发展水平、贸易依存度和产业结构对创新投入两个松弛变量的影响显著为负，政府干预对创新投入两个松弛变量的影响显著为正。因此，有必要在剔除这些环境变量和随机冲击对投入松弛变量的影响后再考察各国创新SBM效率的真实水平。

第二，30个OECD国家和中国的创新数据证明在对环境变量进行调整后，从均值来看，日、韩的创新效率值最高，达到0．74，北美洲次之，欧洲平均创新效率最低。从年度波动情况来看，日、韩出现明显的效率上升趋势，欧洲效率相对较为平稳，而中国在经历2004年低谷之后平均效率开始逐步上升，和各国差距也在逐渐缩小。

第三，在和OECD各国的比较中，中国创新效率和创新能力仍处于较低水平，还有较大的提升空间。中国创新SBM效率在2004年以后有所提升，和各国的差距正逐步缩小。另外，环境因素和随机冲击对中国创新效率的影响比较明显，剔除环境因素和随机冲击的影响后，中国创新SBM效率提升达到15．47%，高于样本国家的平均水平。

[1] 白俊红，江可申，李婧．应用随机前沿模型评测中国区域研发创新效率[J]．管理世界，2009，（10）：51-61．

[2] 史修松，赵曙东，吴福象．中国区域创新效率及其空间差异研究[J]．数量经济技术经济研究，2009，（3）：45-55．

[3] 万坤扬，陆文聪．中国技术创新区域变化及其成因分析——基于面板数据的空间计量经济学模型[J]．科学学研究，2010，（10）：1582-1591．

[4] 于明超，申俊喜．区域异质性与创新效率——基于随机前沿模型的分析[J]．中国软科学，2010，（11）：182-192．

[5] 罗亚非，王海峰，范小阳．研发创新绩效评价的国际比较研究[J]．数量经济技术经济研究，2010，（3）：28-41．

[6] 吴洪，赵桂芹．国际产险业SBM效率研究——基于OECD国家和中国的比较[J]．数量经济技术经济研究，2010，（8）：88-101．

[7] Nasierowski W，Arcelus F J．On the efficiency of national innovation systems[J]．Socio-Economic Planning Sciences，2003，37：215-234．

[8] Wang E C，Huang W．Relative efficiency of R＆D activities：A cross-country study ac-counting for environmental factor in the DEA approach[J]．Research Policy，2007，36：260-273．

[9] Sharma S，Thomas V J．Inter-country R＆D efficiency analysis：An application of data envelopment analysis[J]．Scientometrics，2008，76（3）：483-501．

[10] Fried H O，Lovell C A K，Schmidt S S，Yaisawamgs．Accounting for environmental effects and statistical noise in data envelopment analysis[J]．Journal of Productivity Analysis，2002，17：157-174．

[11] Tone K．A slacks-based measure of efficiency in data envelopment analysis[J]．European Journal of Operational Research，2001，130：498-509．

[12] Graves S B，Langowitz N S．R＆D productivity：A global multi-industry comparison[J]．Technological Forecasting and Social Change，1996，53（2）：125-137．