极坐标系下机器人路径规划算法

李艳辉， 曲萃萃， 樊晓克， 刘彦昌

( 1. 东北石油大学 电气信息工程学院，黑龙江 大庆 163318； 2. 淄博职业学院 电子电气工程学院，山东 淄博 255314； 3.东北石油大学 秦皇岛分校，河北 秦皇岛 066004 )

0 引言

机器人避障问题为机器人研究领域的热点，成果被应用于工业、农业、军事等方面.其主要研究内容为搜索一条从起始状态到目标状态的最优或近似最优无碰撞路径[1-3].李天成等描述一种基于扇形栅格地图的路径规划算法，解决移动机器人静态避障路径规划问题，但采用的模型复杂[4]；朱毅等提出一种基于行为的方法，解决未知环境信息下势场法路径规划的局部极小问题，但计算量大，实时性差[5]；梁瑾等应用并联神经网络结构与模拟退火算法相结合的方法，得到一条最优平滑路径，但计算所需时间较长[6]；Chen M等采用最小化风险和最小化能量消耗为目标函数，研究基于改进蚁群算法的路径规划问题[7]，但不能保证寻得路径最短[8]；遗传算法提供一种求解复杂系统优化问题的通用框架，对问题种类有很强的鲁棒性[9]，被广泛应用于机器人避障研究[10].

考虑机器人避障模型的复杂性、初始种群的多样性及实时性等问题，相对于传统直角坐标系下采用遗传算法进行路径规划[11-15]，笔者提出一种极坐标系下基于遗传算法的路径规划算法.该算法将角度作为编码对象，同一半圆上产生初始种群，可更好地保持种群多样性；引入双避障模式，克服传统算法在寻优过程中避障所引起的时间赘余；在有障碍物模式中采用重启策略，克服遗传算法易早熟的缺点；提出单纯形交叉算子，使子代趋近于最优父代.仿真结果表明：该算法在适应度函数复杂程度、算法实时性、规划的路径长度上优于传统直角坐标系下算法.

1 算法分析

1.1 运动模型

根据机器人及障碍物大小，考虑实际工程情况，作假设：(1)机器人工作环境为静态2维空间半圆区域；(2)将机器人及障碍物视为质点.机器人在2维空间极坐标系下运动模型见图1，其中：K为起点；T为终点；Xi为机器人当前位置.

将K与T连线所在的极轴n等分，中间目标点Xi坐标为(ri,θi)(i=1,2,…,n-1)，其中ri，θi分别为Xi在极坐标下的半径和角度.机器人运动模型表示为

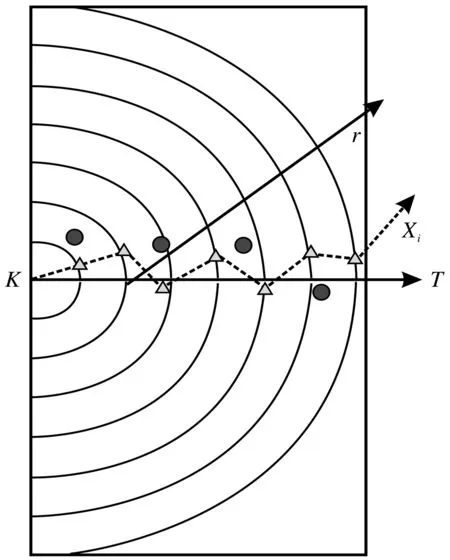
图1 机器人运动模型

(1)

式中：w为同心圆的步长.

研究目的为在极坐标系下采用遗传算法搜索最优中间目标点，将其与起点、终点顺次连接，得到最短无碰撞路径.与传统直角坐标系下路径编码方式比较，极坐标系下路径编码方式把角度作为编码对象，将复杂的二维编码简化为一维编码优化问题.

1.2 双模式路径规划算法

传统直角坐标系下基于遗传算法的路径规划算法，没有根据障碍物位置信息判断下一最优中间目标点是否需要遗传算法寻优获得，使算法寻优时间增加、实时性降低.文中算法分为有障碍物和无障碍物2种模式.

有障碍物模式表示机器人处于有障碍区，采用布尔变量SO表征该模式，SO=1为模式被激活，采用遗传算法作为路径规划算法，在极坐标系下对下一中间目标点角度编码，寻找最优中间目标点.无障碍物模式表示机器人处于无障碍区，采用布尔变量SNO表征该模式，SNO=1为模式被激活，采用直接向目标点行进方式作为路径规划算法，寻找最优中间目标点.2种模式表示为

(2)

当Ci=1(i=1,2,3)时表示事件发生，其中：i=1表示极坐标系下半径为ri的圆周外范围；i=2表示极坐标系下半径为ri-1的圆周内范围；i=3表示极坐标系下半径为ri-1和ri之间的圆环范围.

1.3 适应度函数

适应度函数是影响遗传算法收敛性和鲁棒性的主要因素.机器人路径规划的目的为总路径最短，即要求每段路径最短.机器人第i段路径li可表示为

(3)

式中：θi，θi-1为机器人当前和下一中间目标点的角度.

障碍物位置对适应度函数的影响在初始种群选取时排除，只要θi选取时不与障碍物的安全角度φ相交，机器人即可成功避障.因此，可用li的倒数作为适应度函数f，表示为

f=1/li.

(4)

该适应度函数仅用到1个约束条件，计算简单，避免传统算法中适应度函数多项加权求和引起优化不稳定问题.

1.4 重启策略

避障模式下利用遗传算法寻优时采用重启策略，如果当前代收敛，则随机产生1个新的大小相同的初始种群，此种群保留上一代最优个体，其余个体在整个搜索空间内随机产生.重启策略的判断条件及方式为

(1)判断条件：判断当前种群是否收敛，如果收敛且当前代数小于进化代数g(g为给定值)，则采用重启动策略；

(2)重启方式：保留当前代中适应度最大的个体，随机生成size-1个(size为初始种群中个体数)个体，与保留的最优个体构成新的初始种群.

与传统直角坐标系下采用遗传算法的路径规划算法比较，文中算法采用重启策略可避免早熟现象，保证基因多样性，提高算法收敛速度.

1.5 单纯形交叉算子和自适应变异算子

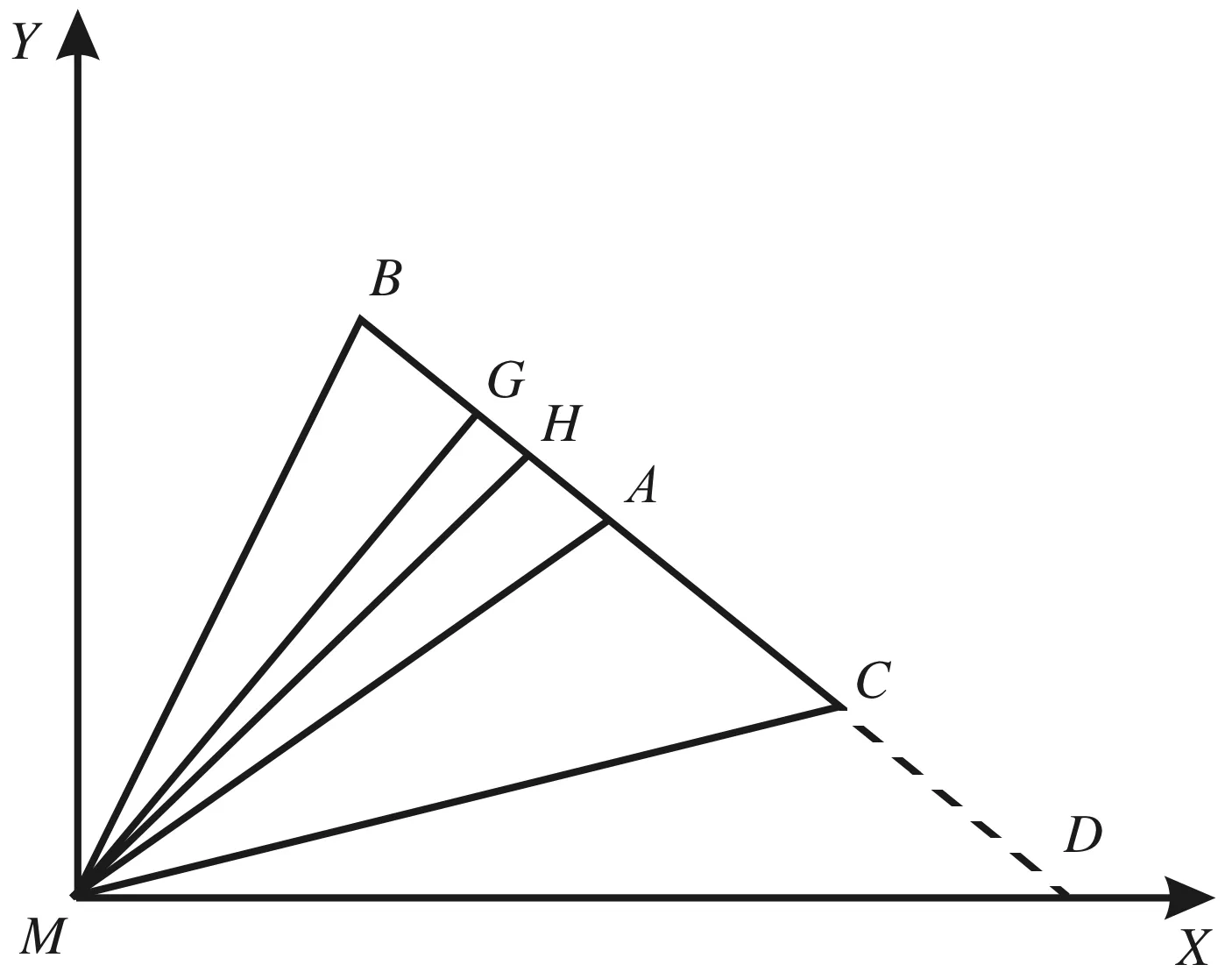
图2 单纯形交叉算子

遗传算法的交叉算子选择借鉴单纯形法思想[16]，提出新的实数单纯形交叉算子(见图2).选择步骤为

(1)当代种群中设概率pc=0.6，选择2个个体(θi,θi+1)，分别为∠CMD和∠BMD，设fθi+1>fθi，交叉后子代趋近于f较大的父代θi+1.

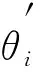
=β(θi+1-θi)+θi,

(5)

(6)

式(5-6)中：β为交叉系数，在0.5～1.0间随机产生.

采用自适应的变异算子对种群进行变异操作，产生新个体pj为

pj=0.10-0.01j/size,j=1,2,…,size.

(7)

传统类似于基因串的遗传交叉方式产生的子代个体无方向性，单纯形交叉算子克服此缺点，使交叉后子代趋近于最优方向.

1.6 算法流程

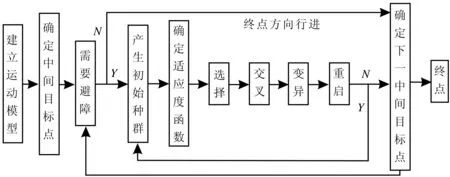
图3 路径规划算法流程

文中基于遗传算法在极坐标系下通过区域内搜索路径，利用选定的适应度函数评估路径长短，进而确定最优路径，算法流程见图3.经过确定中间目标点、避障判断、遗传算法寻优、重启等步骤，得到最短无碰撞路径.

相对于传统直角坐标系下采用遗传算法的路径规划，文中算法在极坐标系下建立运动模型，对角度进行路径编码，路径寻优过程中提出双避障模式，借鉴重启策略及单纯形方法，更好地保持种群多样性，减少寻优时间、多样性，提高算法收敛速度.

2 仿真分析

采用文中算法进行仿真实验，极角坐标系下障碍物坐标与起始点距离见表1，采用双避障模式遗传算法.其他参数设置为：初始种群size=20；进化代数g=100；起点及终点等分数n=50.

表1 极坐标系下障碍物坐标及起始点距离

仿真实验目标点适应度函数曲线和规划路径见图4和图5.由图5可见，采用文中算法机器人避开全部障碍物.

为与直角坐标系下采用遗传算法的路径规划对比，将极坐标系下障碍物坐标转换为直角坐标，采用同样的起始点距离及参数设置.在直角坐标系下利用遗传算法进行路径规划，仿真实验适应度函数曲线和规划路径见图6和图7.由图7可见，机器人未能避开全部障碍物.

设起始距离为100～500 cm时，不同算法仿真实验运行时间及规划路径长度见表2.由表2可见：文中算法寻优得到的路径长度为122.15～520.19cm，与传统直角坐标系采用遗传算法比较平均路径长度缩短20.8%，平均运行时间节省75.9%.对比不同算法仿真实验适应度函数曲线和规划路径，文中算法较传统直角坐标系下算法适应度函数大，寻优次数少，规划路径短，实时性好.

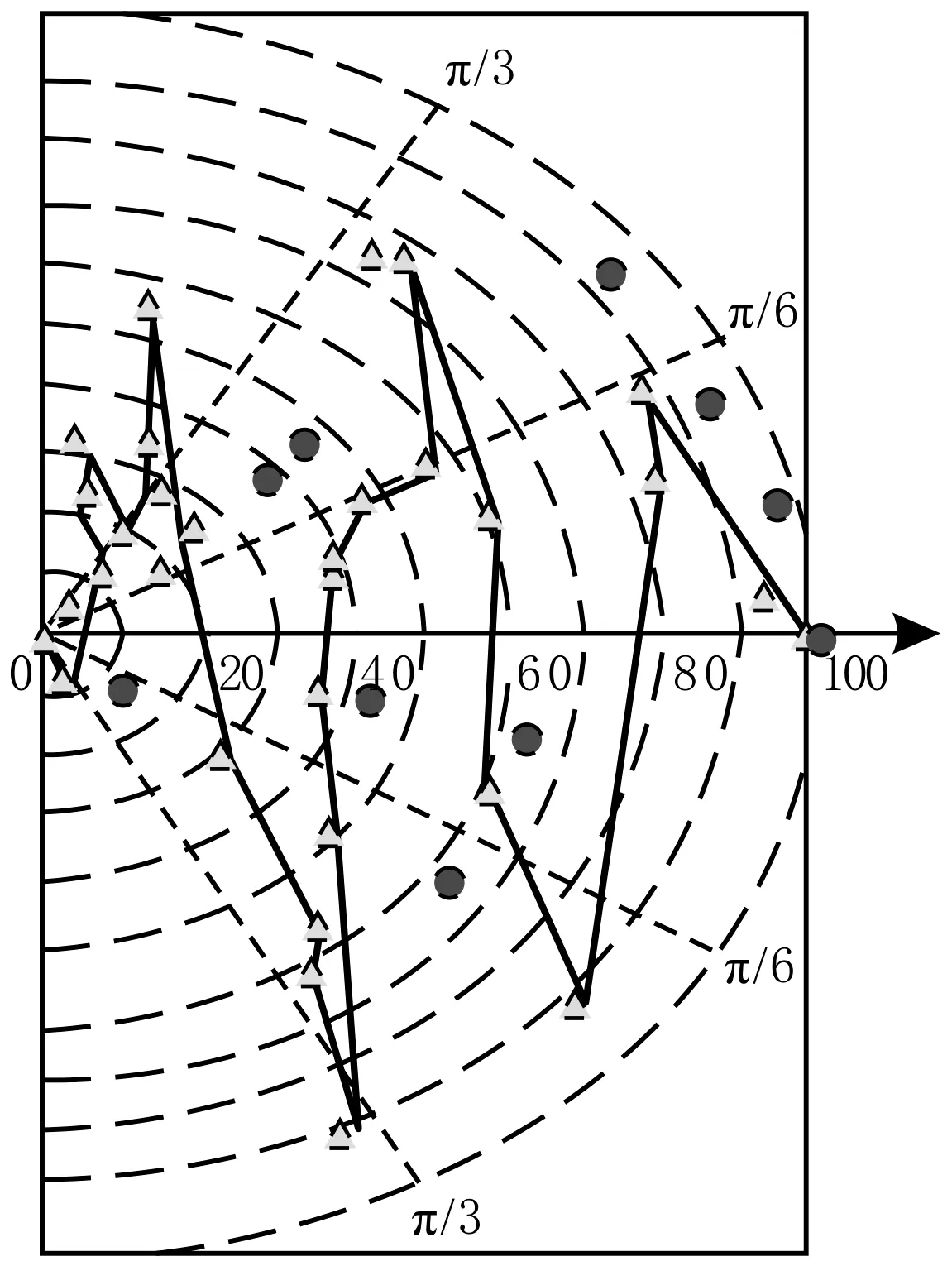
图5 文中算法规划路径

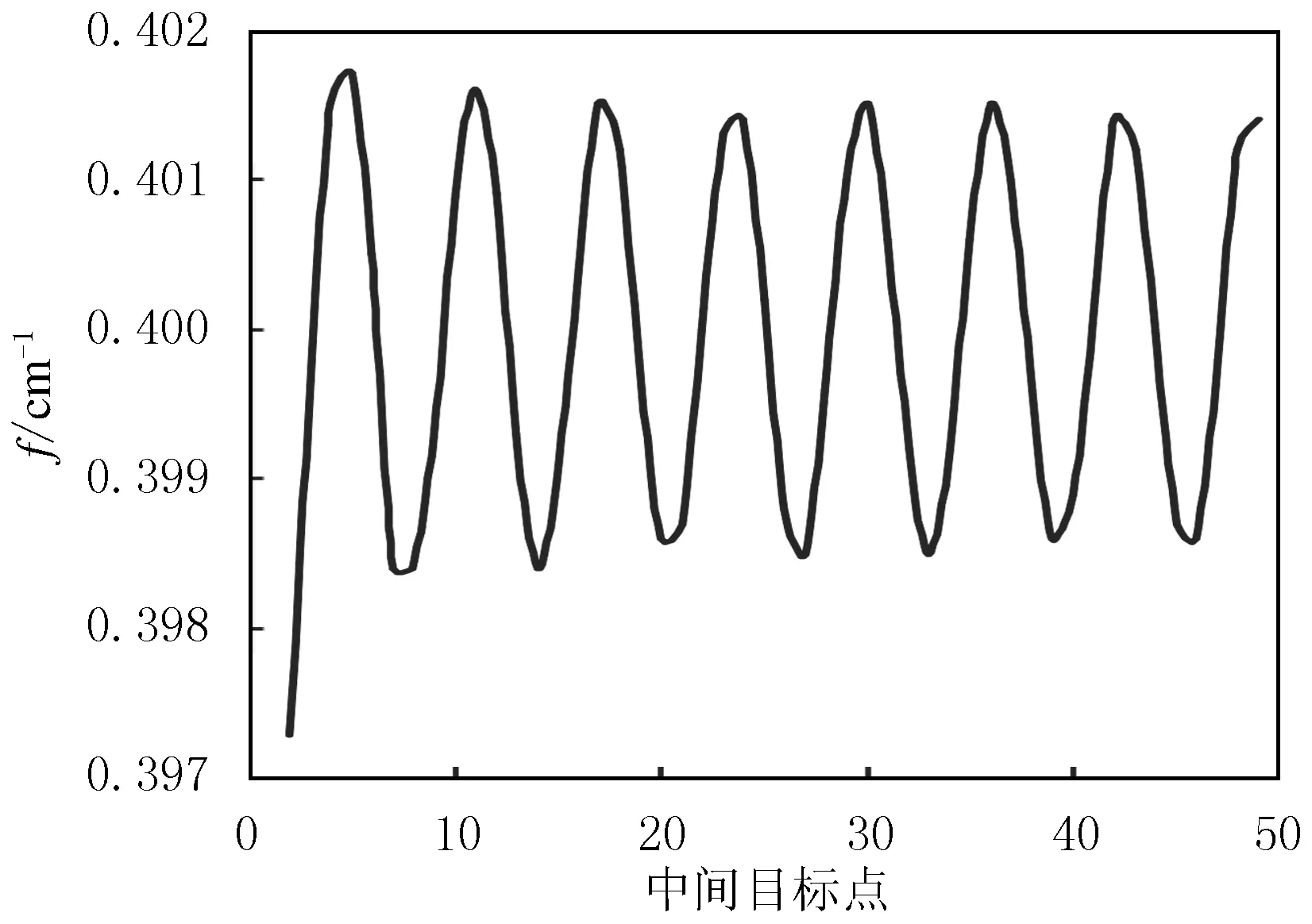
图4 文中算法目标点适应度函数曲线

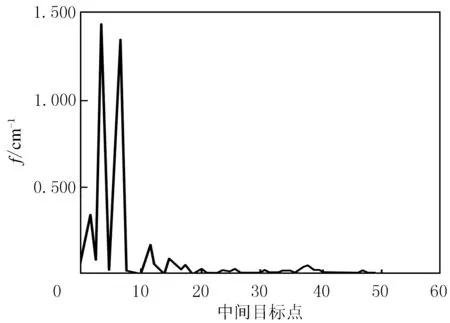
图6 传统算法目标点适应度函数曲线

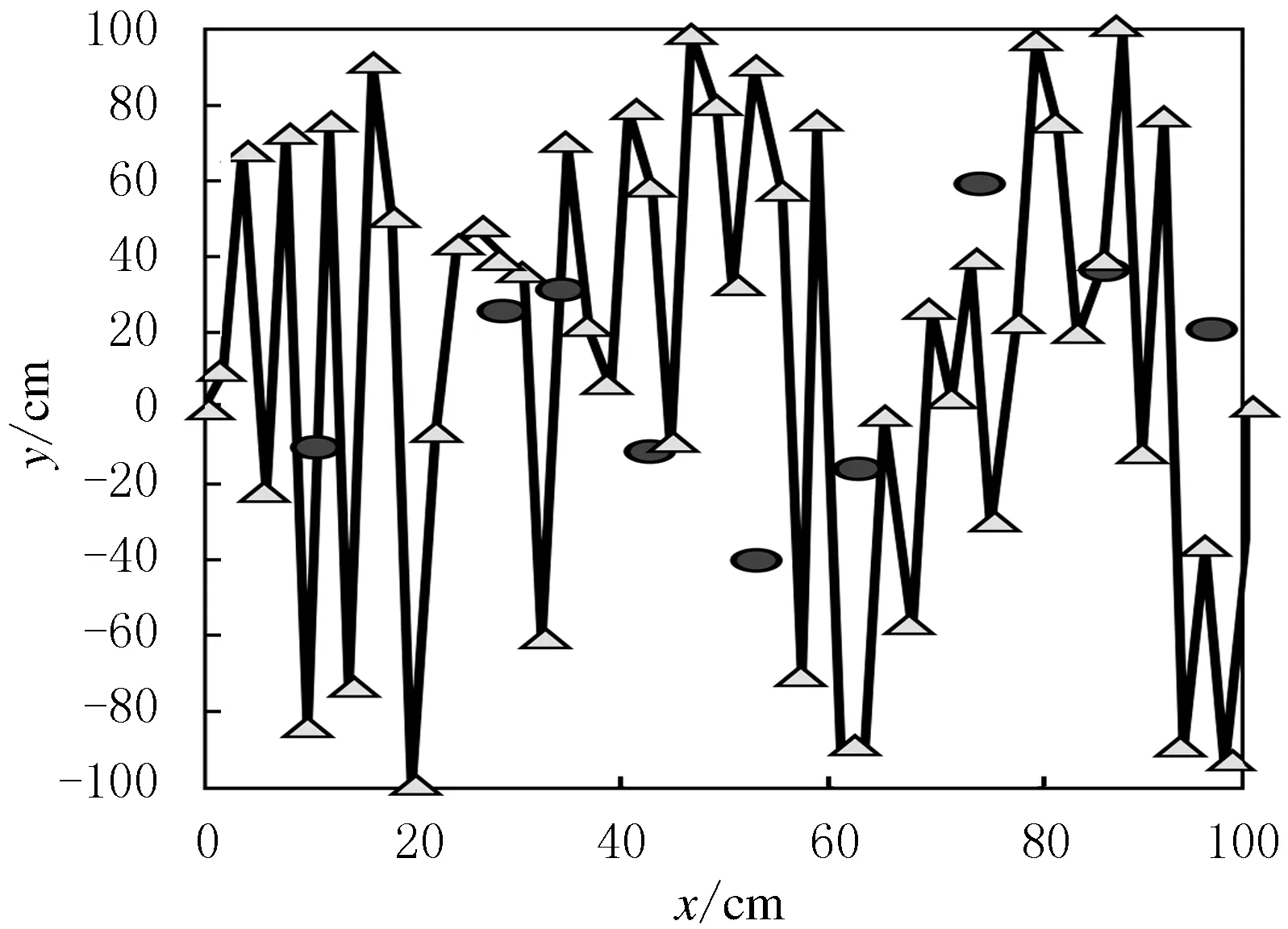
图7 传统算法规划路径

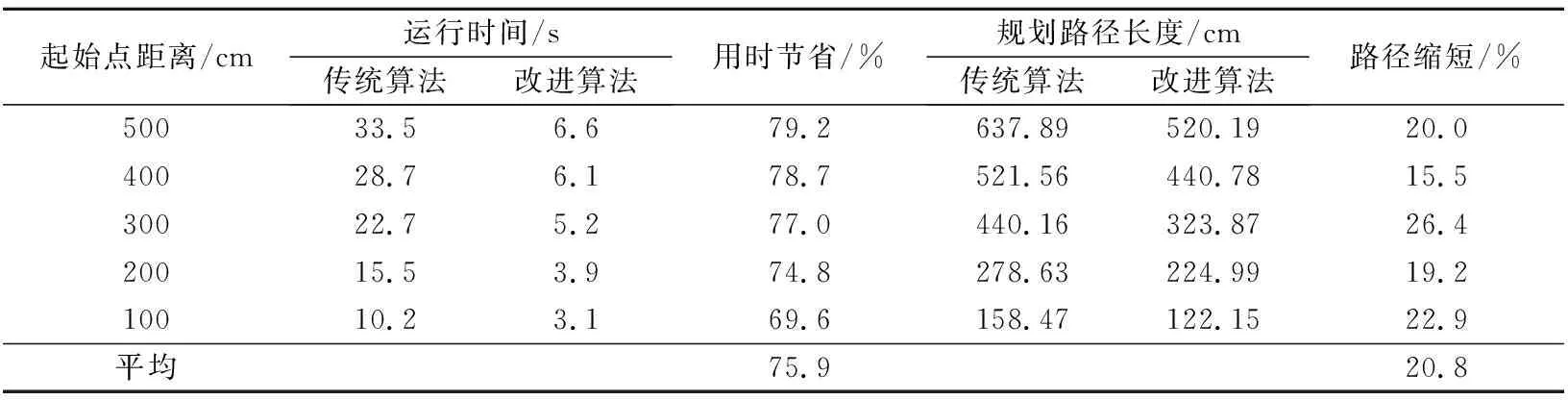
表2 不同算法运行时间和规划路径长度

3 结束语

提出一种极坐标系下基于遗传算法的机器人路径规划算法，应用于机器人路径寻优.算法采用双避障模式，加入重启策略和单纯形交叉算子.与传统直角坐标系下采用遗传算法路径规划结果比较，文中算法规划得到的平均运行时间低于传统算法的75.9%，平均规划路径长度小于传统算法的20.8%.该路径规划算法及2种障碍物模式对解决实际工程中机器人避障和路径规划问题具有一定参考意义.