基于双欧拉模型的流化床气固两相流场数值模拟

朱 博， 王 强， 郭慧军， 张潇玲， 杜明俊

( 1. 辽宁石油化工大学 化学与材料科学学院，辽宁 抚顺 113001； 2. 中国石油集团工程设计有限责任公司 华北分公司，河北 任丘 062552 )

0 引言

目前,对流化床床层内复杂动力学特性的研究，虽然取得一定的进展，但存在许多问题，如气固相间曳力的选择、颗粒相间作用机制、边界条件处理、湍流模型选取等，研究大多依赖经验技术和半经验理论.随着计算机科学及数值分析的不断发展，逐渐形成气固两相流动数值模拟学科，预报流化床工作的全过程，并为工程流态化装置的优化和放大设计提供一种新的手段.

人们对气固流化床内两相流场进行研究[1-8]，并取得一些有意义的成果.Alder B J等[4]首次在分子系统相间扩散数值模拟中提出硬球模型.Moon S J等[5]采用数值方法研究三维振动流化床中黏性颗粒的动力学行为,并发现瞬时振动产生的巨大张力有助于降低黏性颗粒形成的聚团.何成铨[6-7]等研究细粉催化剂在流化床中的密度分布规律，并得出分布图和关系式.Gidaspow D[8]提出把颗粒作为连续相处理的双流体模型，并且成功预测鼓泡床流体力学行为.杨太阳等[9]在双流体模型基础上发展针对气泡的模拟程序，成功模拟鼓泡床中气泡频率、速度、长度特征及颗粒循环状态.

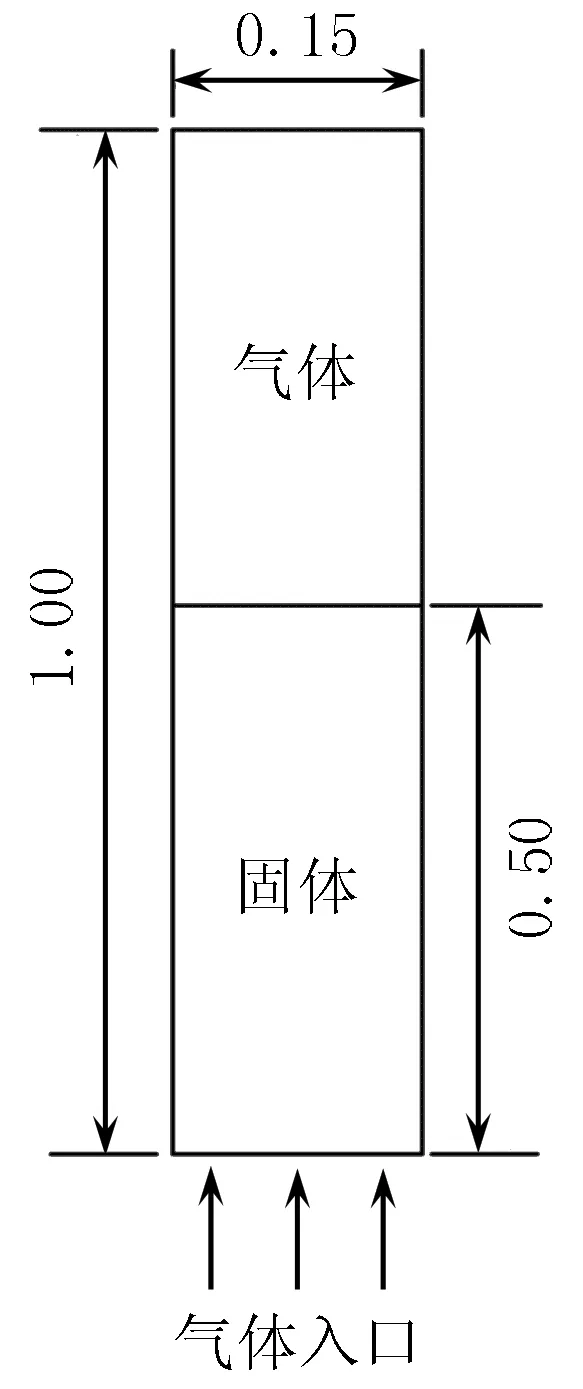
图1 流化床物理模型(单位:m)

对于气固两相流动，相间曳力是表征两相之间相互作用和动量交换的重要参数，决定数值计算总体的准确性[10].对于低流化风速下，采用Syamlal-O’Brien曳力模型计算床内流化过程误差较大[11-12].结合实验数据，笔者对Syamlal-O’Brien曳力模型进行修正，利用FLUENT软件自带的双欧拉模型对均匀床内低速气固两相流场进行数值计算，为进一步改善和推动气固两相流动数值模拟的发展提供依据.

1 模型修正

实验和数值模拟采用高1.00 m，直径为0.15 m带分布板的鼓泡床，入口空气流速为0.25 m/s.顶部压力为标准大气压，固相区充满粒状固体，体积分数为55%，简化的流化床物理模型见图1.利用Gambit进行建模和网格划分.采用结构化矩形网格进行单元划分，并通过床层压降确定模型最适宜的网格数(30 480个).

1.1 数学模型

应用较广泛的气固两相流模型包括欧拉-欧拉拟流体和欧拉-拉格朗日离散相模型，基于计算机资源的限制，大多采用欧拉-欧拉拟流体模型进行数值计算[13-14].在实际流态化过程中，萨夫曼升力对于大粒径颗粒影响较大，对于粒径远小于粒子间距的鼓泡床，可忽略升力对主相流场的影响[14].对于虚拟质量力，当第二相密度远小于主相密度时，虚拟质量影响较大，不能忽略，鼓泡床中第二相颗粒的密度远大于主相气体的密度，因此该项可以忽略[14].采用双欧拉模型对低流化风速下气固两相流场进行数值计算，可以忽略升力、虚拟质量力及壁面滑移边界对流态化过程的影响.

质量守恒方程为

(1)

动量守恒方程为

(2)

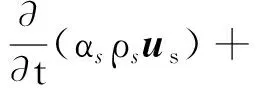
(3)

式中：αv，αs分别为气相和固相的体积分数；uv,us分别为气相和固相的速度矢量；ρv，ρs分别为气相和固相的密度；p为两相共享压力；τ为压力应变张量；Rvs，Rsv分别为气相和固相间曳力；分别为气相和固相间质量传递；usv，uvs分别为气相和固相间速度；g为重力加速度.

1.2 修正Syamlal-O’Brien阻力模型

最小流化速度是指流化床层开始流化时的气体空床线速.原Syamlal-O’Brien阻力模型计算的最小流化速度为0.21 m/s，不能满足低速流化床相间阻力的计算，结合实验数据，重新对相对雷诺数和曳力系数进行界定，对原有的Syamlal-O’Brien阻力模型进行修正，使其满足低速流化过程.

曳力f计算模型为

(4)

式中：CD为曳力函数；Res为相对雷诺数；vr,s为固相沉降速率.

曳力函数CD采用Dalla Valle给出的形式：

(5)

这个模型是基于流化床或沉淀床颗粒的末端速度的测量，并使用体积分数和相对雷诺数的函数关系式：

(6)

式中：ρl为液相黏度；ds为固相颗粒直径；vs为固相速度；vl为液相速度；μl为液相黏度.

液—固交换系数Ksl为

(7)

式中：αs,αl分别为固相和液相分数.

固相自由沉降速度系数为

(8)

1.3 边界条件

计算时，固相颗粒密度为2 600 kg/m3,剪切黏度为1.789×10-5Pa·s,粒径为0.2 mm,气相密度为1.2 kg/m3，剪切黏度为1.89×10-5Pa·s.

入口边界条件为

出口边界条件为

2 数值模拟

实验装置由流化床和辅助设备组成，静床高度为1.00 m,直径为0.15 m,固体颗粒采用Geldart B类颗粒，空气为流化气体，实验在常温常压下进行，实验装置及流程见图2.通过实验测得最小流化速度为0.80 m/s.

数值计算采用FLUENT 6.3软件，并对其进行二次开发，利用C语言编写UDF程序实现修正后Syamlal-O’Brien模型的计算过程，采用一阶迎风格式对控制方程进行离散，利用Phass Coupled SIMPLE算法进行求解，迭代步长为1 ms,修正压力和速度的松弛因子，使其快速收敛.

稳定进气10 s后流化床轴向压力变化的实验结果与计算结果见图3.由图3可知，采用修正Syamlal-O’Brien曳力模型计算结果小于实验结果，但轴向压降变化趋势相同，这主要是受固体颗粒球形度的影响.对比计算结果和实验结果，最大相对误差为4.4%，满足工程实际要求，修正模型能够描述低速气固两相流动相互作用物理过程.

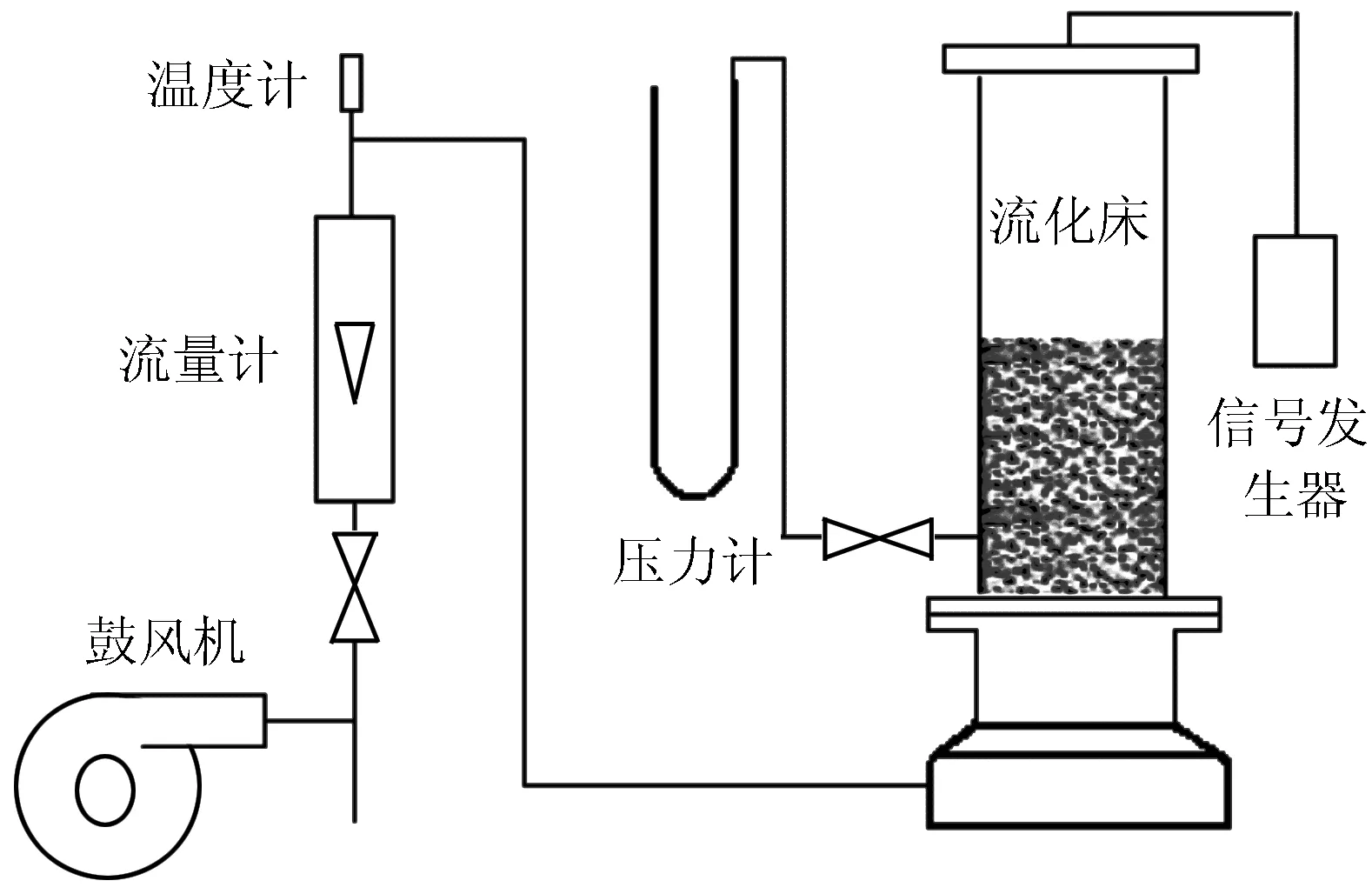
图2 流化床实验装置及流程

图3 10 s后流化床轴向压力变化曲线

Syamlal-O’Brien阻力模型修正前后不同时刻流化床固相颗粒体积浓度云图见图4.由图4可知，修正前模型在0.8 s后开始出现气泡，且随着时间延长，气泡不断上升并长大；修正后模型在1.4 s后逐渐产生气泡，且气泡增长和上升速度较慢.对于固相颗粒，修正前模型在1.5 s前均匀膨胀，之后在床底不均匀气流的脉动下，开始出现不均匀膨胀，且密相床层高度随之降低；修正后模型在2.0 s前上部颗粒均匀膨胀.流态化初期，密相床层轴向上存在速度差，导致高度方向上流态化气速大小不一，较低的气速使流化床床层发生均匀膨胀，较高的气速导致气泡生成.由于计算所用颗粒直径为0.2 mm，属于流态化原理中Geldart B类颗粒，该类颗粒在流态化气速较小时流化床床层先发生均匀膨胀而无气泡生成，随着流态化气速增大至鼓泡速度时才出现气泡.修正后模型计算结果与流态化原理[15]导出的结论一致.

稳定进气2.0 s后不同介质流化床轴向压力变化曲线见图5.由图5可知，靠近床层底部一定区域，修正后的曳力模型计算的固相和气相床层压力大于原模型的，且随床层高度的增加压力逐渐降低，主要是修正曳力模型计算的气泡聚并与破裂频率降低引起的.流化床床内压力场的分布受气泡状态及进气气流影响，采用原曳力模型计算的固相介质和气相介质的轴向压力波动较大，主要原因是修正前模型计算的最小流化速度偏大，短时间内出现大量气泡，随着气泡的不断上升、融合和破碎，使固相区出现不均匀膨胀，从而导致床层压力开始大幅度不规则波动，此时床层压降受脉动气流频率和气泡行为共同控制.修正后模型计算压力波动的范围较小，主要原因是初始流化速度小，床层压力主要受脉动气流波动控制，使床内固相颗粒均匀膨胀.

图4 不同时刻流化床固相颗粒体积浓度云图

图5 2.0 s后不同介质流化床轴向压力变化曲线

3 结论

(1)结合实验数据，对体积分数和相对雷诺数进行重新界定，修正Syamlal-O’Brien曳力模型，使其最小流化速度为0.80 m/s,满足低流化风速条件.

(2)结合修正后曳力模型，采用双欧拉模型对均匀床内低速气固两相流场进行数值计算，计算结果比实验数据略小，最大相对误差为4.4%，满足工程实际要求.

(3)由于Syamlal-O’Brien阻力模型是根据床层压降、表观气速、床层膨胀比等实验数据得到的半经验公式，是在单个颗粒曳力模型的基础上引入颗粒体积分数描述对周围颗粒的影响，建议结合实验，根据数学理论和数值模拟等继续完善一个相对完整的阻力模型.