大型起重船波浪中的运动响应

陈 亮, 张 城, 张小雅

(1.沪东中华造船集团有限公司,上海200135;2.上海船舶运输科学研究所,上海200135)

0 引 言

起重船作业过程是一个极其复杂的过程,在短时间内吊数千吨重物,按中国船级社规范,吊重的重心要算在吊钩以上的滑轮轴上,该点距水面上百米,使全船的重心瞬间提高。全船的横摇惯性半径及浮态都会发生变化。以1 600 t起重船作业工况为例(艉吊1 600 t、吊钩幅度28 m),研究其运动规律。对于起重船有吊重的运动计算,通过BV船级社开发的Hydrostar软件来实现。

1 计算对象

为了更好地说明大型起重船运动特点,采用Hydrostar软件对某大型起重船的运动进行了详细计算和分析。该船总布置图见图1。

该船主尺度:

船长 Lpp=102.0 m;

型宽 B=36.0 m;

型深 D=10.0 m;

调遣吃水 d 1=6.50 m;

作业吃水 d2=6.50 m;

结构设计吃水 d s=7.00 m;

方型系数 Cb=0.955。

2 计算内容

本船用于近海、沿海、内河和港口水域作业。其中,工作环境限定有义波高≤2.5 m,风速≤13.8 m/s。

计算工况:作业工况艉吊1600 t,吊钩幅度28 m。

计算条件:波浪传递函数计算时,波浪频率位于0.1 rad/s～2.0 rad/s之间,间隔0.1 rad/s,共20个频率。浪向位于 0°～180°之间,间隔30°,共7个浪向,其中0°为迎浪方向。

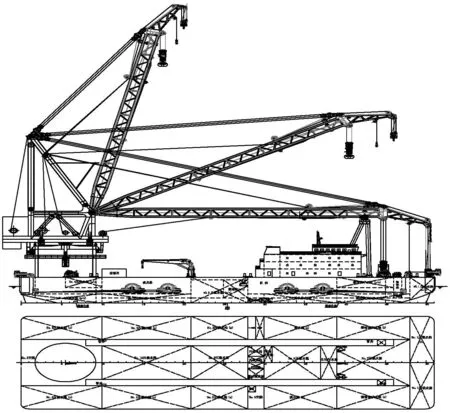
图1 总布置图

3 起重船作业工况下的运动计算

3.1 关于作业工况下起重船的横摇惯性半径的计算

计算横摇惯性半径要计算横摇惯性矩。横摇惯性矩是由船体本身惯性矩Ixx和附加惯性矩J xx两部分组成,其中:Ixx取决于船体的质量分布;J xx主要取决于船体水下的形状及中心位置等因素。工程上通常用经验公式[1]进行估算。由于起重船是一种特殊船型,它大而浅,且船体上层还有臂架和吊重,横摇惯性矩和横摇惯性半径不能采用传统的经验公式,现根据船体的实际质量分布,对每个舱室以及船体结构分别进行计算。惯性矩换算成船体的惯性半径。计算得船体的全船横摇惯性半径

在起重船作业过程中,要考虑1 600 t吊重摆动产生的非线性效应以及钢丝绳的柔性连接,这里作了简化处理,不考虑1 600 t吊重与钢丝绳的柔性连接。

根据经验公式[2]计算常规船横摇惯性半径约为0.33 B。由式(1)算得起重船横摇惯性半径为0.42 B。所以,起重船的横摇惯性半径比常规船要大。

同理,可计算得全船的纵摇惯性半径为0.316 L,根据经验公式计算:常规船在满载状态下,纵摇惯性半径为0.25 L;压载状态下,纵摇惯性半径为0.28 L。所以,起重船的纵摇惯性半径比常规船要大。

3.2 关于作业工况下起重船阻尼系数的确定

因为阻尼是影响运动幅值的重要因素,特别是横摇阻尼的大小是影响计算横摇角大小的主要原因,能否合理地预测横摇阻尼,是准确预报船舶运动的关键之一。人们为此做了很多研究工作,提出过不少方法去估算横摇阻尼,这些方法大致有试验方法、理论计算或经验公式。横摇阻尼估算方法由于黏性较大,至今尚未提出十分合理的阻尼计算理论,只能得到一些近似或定性的结论。下面简要介绍涉及到文中计算的横摇阻尼的一些估算方法。

3.2.1 传统的横摇阻尼修正公式

首先针对常规船,传统的横摇阻尼修正采用驳船经验公式:

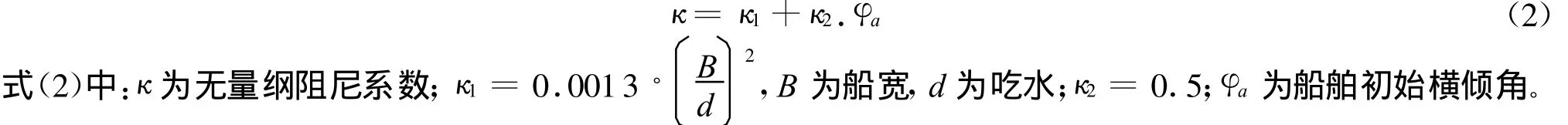
由公式(2)可看出,驳船经验公式为线性。

3.2.2 横摇阻尼

起重船的宽度吃水比B/d远远超过常规船舶,一般起重船为6～14,而常规船为2～3;所以起重船的横摇阻尼和纵摇阻尼也较常规船大。在Hydrostar中,阻尼系数不再按常规的驳船经验公式,对于阻尼系数要重新进行计算。

[3]对线性横摇力矩与横摇阻尼系数的推导关系进行横摇阻尼的计算。在最简单的理想情况下,规则波横浪中,横摇运动表达式为

横摇力矩方程为

由于在考虑横摇力矩时,只考虑线性关系,所以忽略横摇复原力项,线性的横摇力矩方程为

式(4)、式(5)中:Md通过Fluent软件加载横摇运动来计算。横摇力矩整合了剪切力和压力来获得计算结果。即

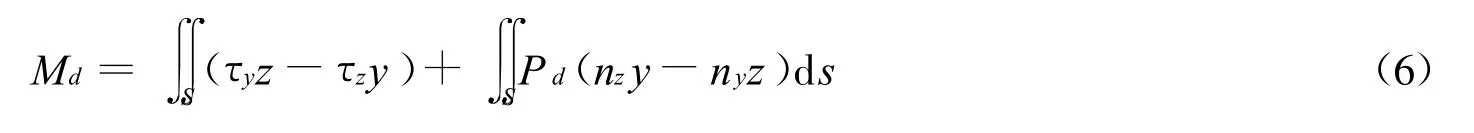
式(6)中:τ为剪力;Pd为动压力。

由式(3)、式(5)、式(6),A和B可以根据傅里叶变换计算得

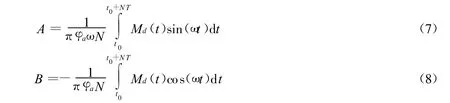
式(7)、式(8)中:A为惯性矩系数;B为阻尼系数。

由于线性化横摇阻尼系数B与未知的横摇角幅值φa有关,因此,求解船舶横向运动响应时需要经过反复迭代计算。

3.2.3 Fluent软件计算横摇一阶阻尼

根据以上理论,通过数值模拟的方法,应用Fluent软件来计算最大横摇角情况下的横摇静水阻力。首先利用Fluent软件建立起重船的动网格模型,通过C++编辑User Defined Function,将横摇运动加载到Fluent中。在一阶线性阻尼中,阻尼系数按临界阻尼相对值取得,一阶阻尼系数通常为临界阻尼的3%～8%。由计算结果可知横摇阻尼系数取临界阻尼的4.38%,纵摇阻尼系数取临界阻尼系数的8%。计算横摇阻尼的步骤:

考虑到Fluent计算的简便,把模型缩小到1/20,即缩尺比λ=20。根据Hydrostar计算缩小到1/20的模型,初始横倾角 φa=4.6°,圆频率ω=2.61 rad/s,周期 T=2.4 s。在Fluent中取迭代时间步长为0.001 s,每1步迭代20次。在1个周期中需要计算2 400步。在Fluent中建立动网格模型,通过C++编辑User Defined Function,将横摇运动加载到Fluent中。下列程序:0为x方向;1为y方向;2为z方向。

以上是User Defined Function的主要部分。由此可看出,加载到模型中的横摇运动相当于是一个角速度,也就是对船壳加载一个角速度。在Fluent中设置此模型为两相流模型,水线面以上为空气,水线面以下为水。文中进行了1.5 T的迭代计算,并对数据进行了处理。以上计算过程见图2和图3。

图2 残差曲线

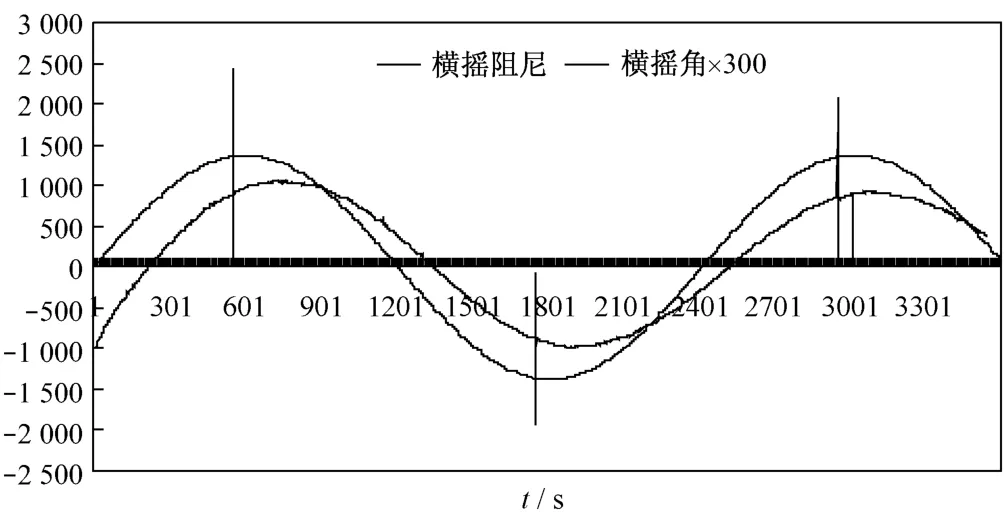
图3 横摇力矩与横摇角

图2 中,残差曲线横坐标表示迭代的步数,纵坐标表示每1步迭代完后的残差值。

图3中,横向坐标为10-3s。为了研究横摇角与横摇阻尼之间的变化关系,横摇角数值乘以300保证量级与横摇力矩一致,并将两者放到同一坐标系中。对于横摇角而言,纵坐标表示度数,对于横摇力矩而言,纵坐标表示力矩大小。由图3表明,横摇力矩和横摇角均呈周期性变化;当横摇角达到最大值时,此时的横摇力矩不一定最大。

求得横摇阻尼系数2 644 N·m,横摇阻力554 N·m·s/rad。

一阶阻尼根据不同船型应取不同值,Hydrostar建议一阶阻尼是取临界阻尼的3%～8%。Hydrostar计算得此模型的临界阻尼为1.265 1×104N·m·s/rad。

由此,可分析得一阶横摇阻尼是临界阻尼的4.38%。

3.2.4 二阶阻尼计算

在二阶阻尼中,横摇阻尼和纵摇阻尼均按照规范[3]规定的公式选取:

式(9)中:ρ为流体密度;B为船宽;L为船长;CD为系数,范围为0.04～0.1。

在本次起重船作业工况中,横摇二阶阻尼的系数CD取0.04,纵摇二阶阻尼的系数,CD取0.08。

3.3 作业工况运动响应结果

Hydrostar计算起重船作业工况的运动响应结果见表1和表2。

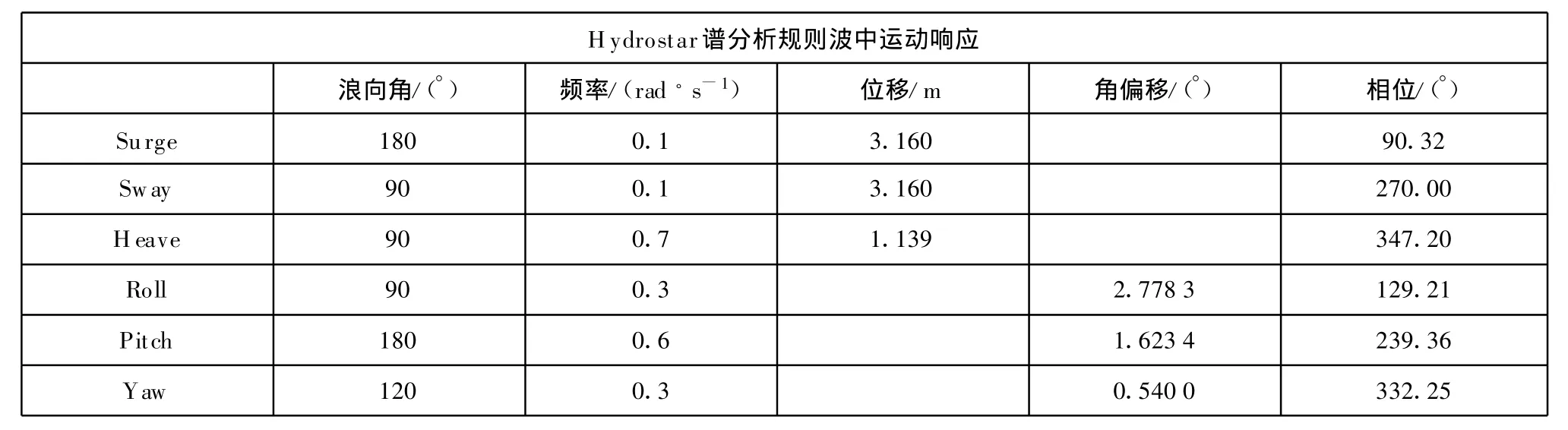
表1 规则波中单位波幅下运动响应

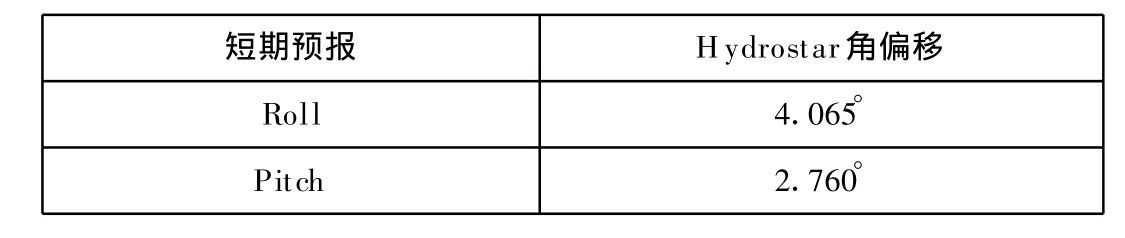
表2 运动短期预报结果

短期预报:在有义波高 Hs=2.5 m时,对应于h1/1 000(超越概率为3.79×10-4)的横摇角为 4.065°,纵摇角 2.760°,此时横摇固有周期T0=23.237 s。

4 结 语

用Hydrostar软件进行作业工况下的运动响应计算,横摇在横浪状态达到最大,纵摇在迎浪时达到最大。运动计算结果均符合规范对起重船运动的规定。

起重船惯性半径和阻尼系数对全船运动产生很大的影响。由于自身的船型特点,采用流体力学的方法可以更准确地计算起重船惯性半径,计算结果可知它的全船惯性半径比常规船要大;阻尼系数对全船运动幅值产生较大的影响。采用Fluent软件对起重船作业工况下的阻尼系数进行了计算分析,合理预测出了横摇阻尼。

5 展 望

该项研究工作无论是在理论上还是在实际工程中都有一定的应用价值,今后拟在以下几方面作进一步研究:

1.由分析可知,在迎浪时,升沉和纵摇最为严重;横浪时,横摇最为严重。实际起重船在运行过程中,耦合状态下的运动响应要远远大于非耦合状态,因此,计算起重船运动过程中必须要考虑耦合影响。

2.由于问题的复杂性,计算起重船作业时忽略了起重船在作业工况下吊重摆动对全船运动的影响。实际作业起吊重物的过程中,需要考虑吊重对摆动产生非线性效应、吊重与钢丝绳之间的柔性连接及吊重还会发生混沌振动等问题。所以,下一步工作应该把吊重的运动与全船的运动结合起来,考虑吊重系统与船体运动之间的耦合作用,使作业工况运动的计算更接近于真实情况。

参考文献

[1] 中国船级社.船舶与海上设施起重设备规范[S].北京:中国船级社,2007.

[2] 李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007.

[3] 谢楠,Dracos VASSALOS,LEE B S.舭龙骨柱体的横摇阻尼的粘性流计算[J].船舶力学,2007,11(6):839-847.