三体船横摇惯性半径的估算方法研究

周立师 段文洋

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

1 引 言

近年来，特种排水型高性能船舶的研究趋于活跃，如深V型船、小水线面双体船以及穿浪双体船等，都是研究和使用较多的船型，同时，三体船也引起了人们极大的关注。三体船船型的特殊构造使得高速三体船的兴波阻力小，2个侧体又能提供足够的稳性，且连接桥还具有提高总纵强度的功能，同时也有利于形成宽阔的甲板面，为设备布置提供更大的空间。此外，该船型还具有优良的耐波性，尤其是可避免双体船的“扭摇”（横摇与纵摇的耦合摇摆）与“急摇”（短周期的横摇），并可明显减小纵摇和升沉［1-2］。由于三体船具有这些突出的优点，其特性研究便成为焦点［3-4］。三体船的横摇性能与三体船的稳性关系极大，而横摇惯性半径正是横摇问题的关键参数之一［5］。

对于单体船的横摇惯性半径的估算值是其船宽的0.30～0.40倍。对于大部分甲板上没有货物或压载的船舶来说，质量主要集中在船体两侧，对于甲板上有货物或压载的船舶而言，货物的质量分布对惯性半径的取值有很大的影响，因此船舶在满载情况下的惯性半径值要小于空载情况。值得注意的是，如果把船舶简化成一根长、宽、高与船的长、宽、吃水相同且质量均匀分布的梁，其横摇惯性半径的解析值为 0.29 倍的船宽［6］。可见，简化的单体梁模型的横摇惯性半径与实际船的横摇惯性半径的取值很接近。也就是说，单体船横摇惯性半径可以简化为质量均匀的单体梁模型横向惯性半径乘以小的修正系数。基于这一观点出发，本文将三体船简化为等效的三体梁模型，通过对三体梁简化模型的研究，给出三体船横摇惯性半径的估算公式。

2 三体船的发展

三体船概念已有较长的历史。上世纪60年代开始开展理论性研究，70年代，前苏联便对三体船的深、浅水阻力进行了理论研究，随后，国外又发表了一些有关三体船方案分析和模型试验的文献。至90年代，这种新船型开始得到厂商的青睐，并有少量实船开始营运，如爱尔兰的“冒险家”号。从90年代中期开始，该船型开始受到国外军方的重视。

目前，已经有不少三体船投入使用，如澳大利亚建造的三体旅游船CatNo.1号（该船在7级风、浪高2.5 m的海浪下能消除船首砰击，可有效减少船在浪高 2.5 m 以上的海浪中的纵摇运动［7］）、澳大利亚的西澳大利亚造船厂建造的世界上最大的AutoExpress127级Benehijigua Express三体船、英国建造的一艘三体试验舰“海神”号和美国三体船军舰“独立号”（已交付海军）。表1所示为检索到的国内外建成和在研的三体船主尺度列表。

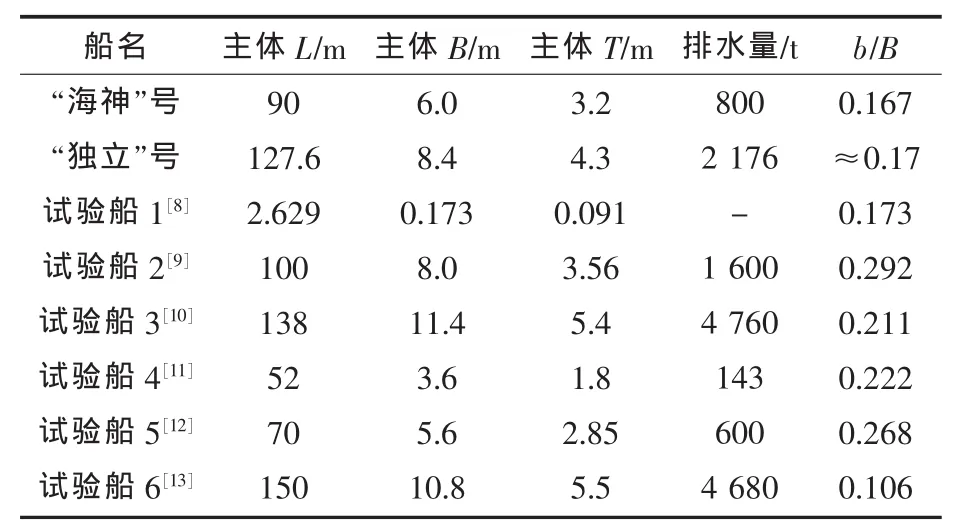
表1 目前建成或试验的三体船主尺度Tab.1 Principal dimensions of trimarans built or tested currently

上述三体船在运行和试验中都表现出了良好的快速性、机动性和稳性。

3 三体船横摇惯性半径的估算

估算单体船的横摇惯性半径时，是将船体简化为一根长梁，通过修正长梁的惯性半径得到估算值。当忽略三体船主侧体连接甲板上的重量时，即假定三体船的所有重量是均分在主侧体上，则可以将三体船简化为三根独立的梁。在简化后的三体梁模型中，主体梁长L、宽B、吃水T，侧体梁长 l、宽 b、吃水 t，主侧体间距为 d（图 1）。

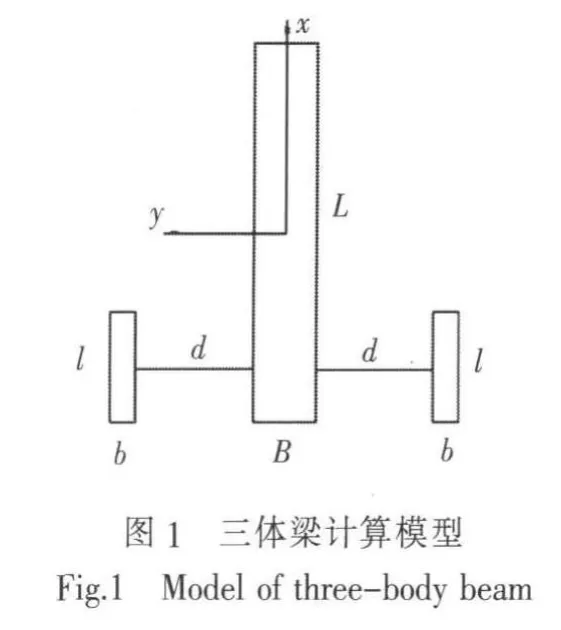
该三体梁的惯性矩可应用材料力学方法求得。单体惯性矩：

式（1）～式（4）中，ρ为质量密度；Δ、Δs分别为三体梁体积和单个侧体梁体积；d为图1所示的主侧体间距；Ixxc为主体惯性矩；Ixxs为侧体惯性矩；It为侧体移轴惯性矩。

由式（4）可知，三体梁的横向惯性半径与主体梁的主尺度、侧体梁的主尺度和主侧体梁的间距有关。对于单体梁模型，横向惯性半径是其船宽的0.29倍，呈一定的线性关系。本文假定的三体梁也是质量均匀分布的，主体和侧体的质量分布均正比于各自的船宽，因此，假定三体梁的横向惯性半径与其总宽度相对应的关系为：

式中，B′为三体梁的总宽，B′＝B＋2b＋2d。

式（5）中的系数α和δ随侧体船宽与主体船宽的比值b／B变化。通过调研已建和试验的三体船，发现 b／B 一般为 0.15～0.3。 表 2 给出了 b／B的范围为 0.10～0.55 时，对应的系数 α 和 δ的取值。

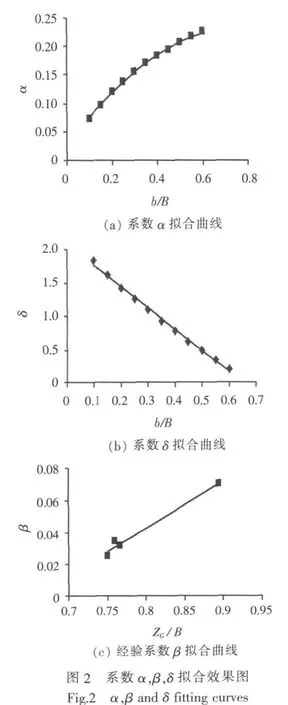
通过对表2中数据进行数值拟合得到的α和δ的估算公式见式（6）和式（7），拟合效果如图 2所示。

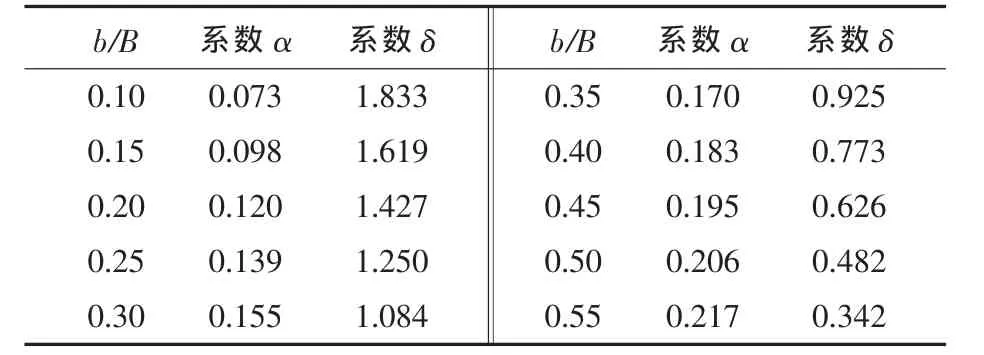
表2 系数α和δ的取值Tab.2 Values of α and δ

4 算 例

本文以4艘三体船为例，采用估算公式计算了其横摇惯性半径，其主尺度如表3所示。

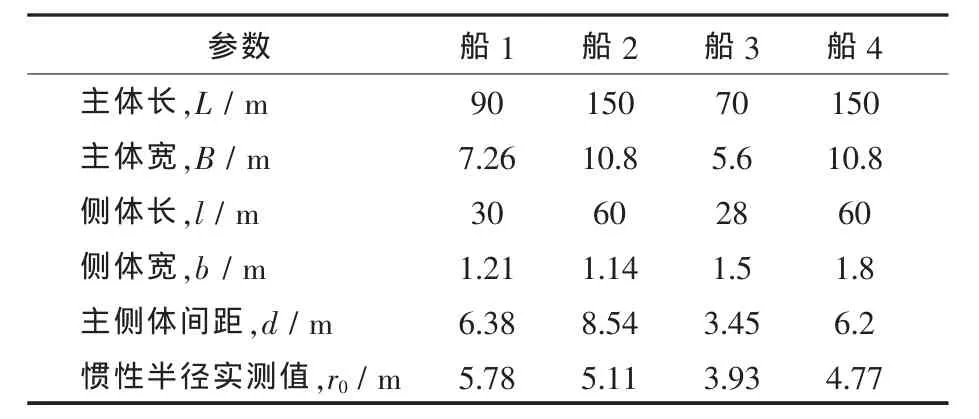
表3 本研究的三体船主尺度Tab.3 Principle dimensions of the trimarans

4.1 三体梁主尺度对横向惯性半径的参数影响

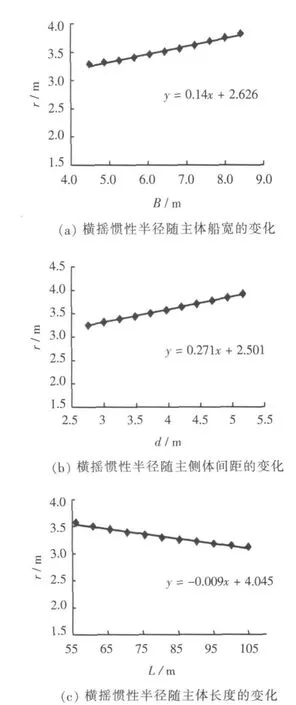
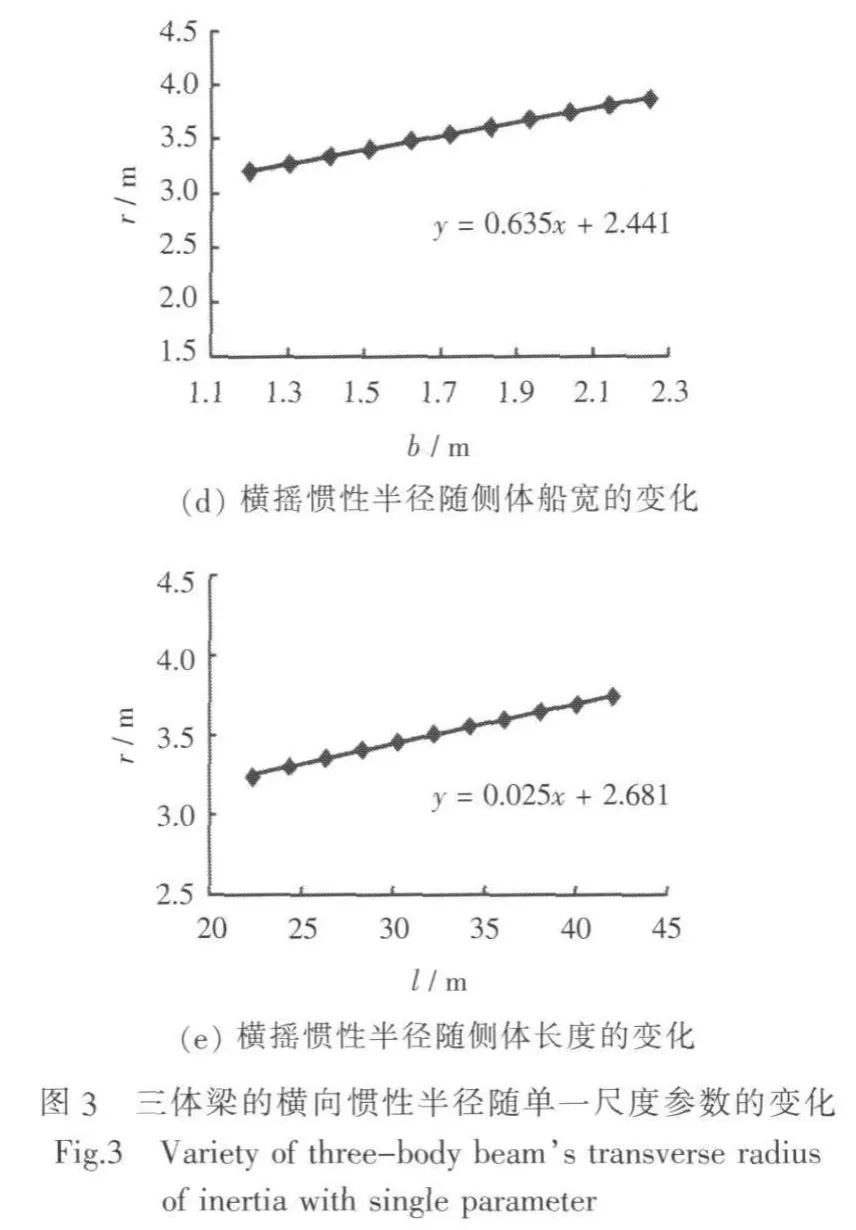
将某一艘三体船简化为3根独立的梁，研究该三体梁的横向惯性半径随单一尺度参数变化情况，如图3所示。图中数据点按式（4）计算，并经线性拟合得到各直线方程。

经研究发现，侧体梁宽、主侧体梁的间距以及主体梁宽是影响横向惯性半径的主要因素，且其随侧体梁宽的变化尤为明显。因主侧体梁的长度对横向惯性半径的影响微小，故先前假设的三体梁横向惯性半径仅与梁的宽度方向相关是成立的。

4.2 三体船横摇惯性半径的估算

应用式（8）对表3中4艘三体船的横摇惯性半径进行了估算，其结果如表4所示。

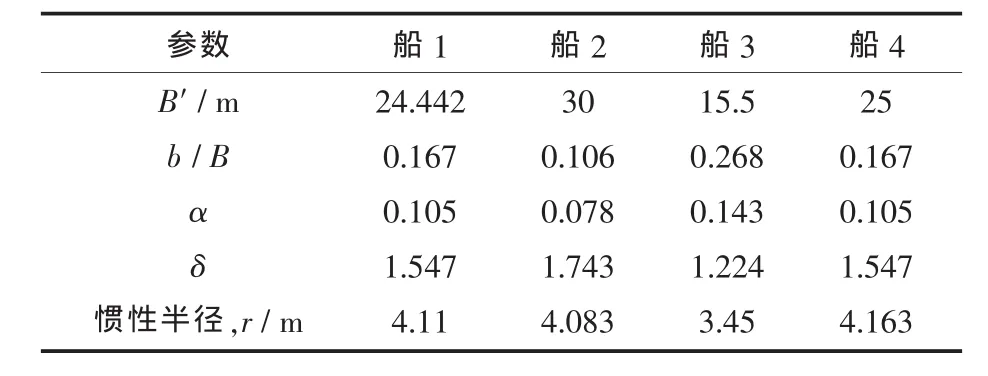
表4 本研究的三体船横摇惯性半径计算结果Tab.4 Results of inertia radius of the trimarans

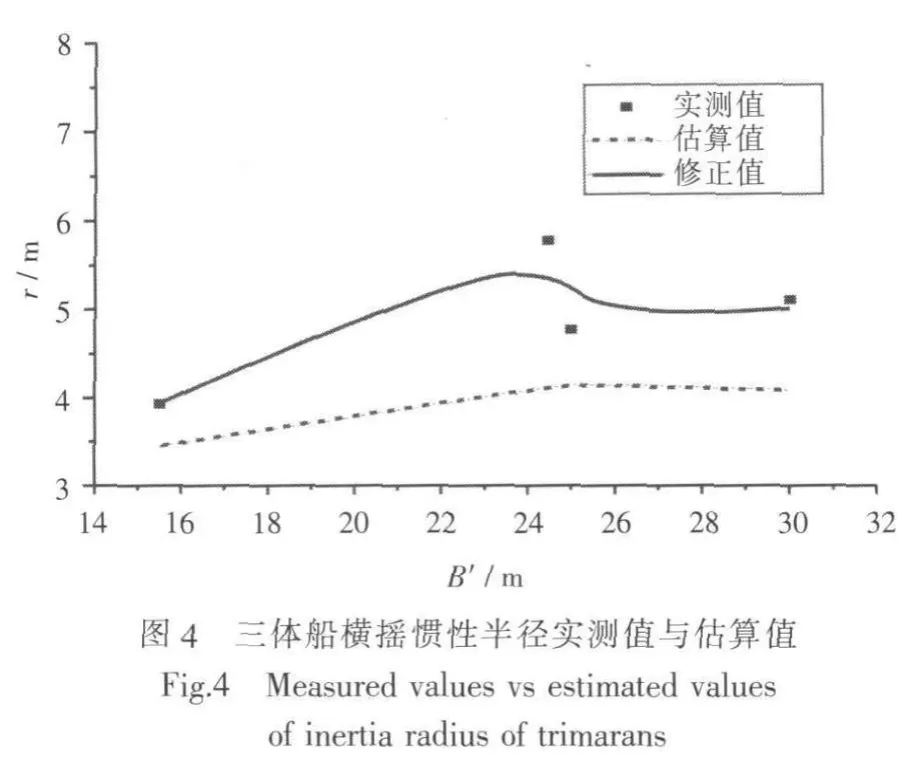
由图4可看出，用式（8）估算的横摇惯性半径值与实测值存在一定的差距，这是因为三体梁模型是假定质量沿各个方向均匀分布，而实际上船舶形状并不像梁一样规则，质量分布沿长度、宽度和水深方向都有一定的变化。并且，由于三体船的特殊结构，其部分压载分布于连接桥和两侧体上。因此，式（8）在估算三体船横摇惯性半径时与其实测值存在一定差距，一般情况下是小于其实测值。故本文在式（8）的基础上引入修正系数β来解决这一问题。即

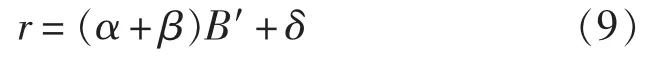
通过研究发现，修正系数β的取值与三体船的重心高度ZG和主体船宽B有关。建议的β取值公式见式（10），β值拟合图见图2c。当然，由于试验数据有限，β的取值还存在一定的局限性，这在以后的研究工作中还有待进一步的完善。

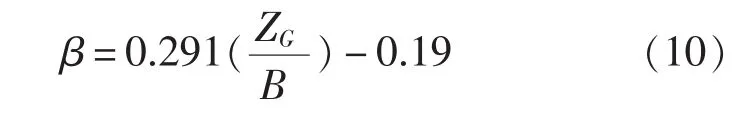
最后，给出三体船横摇惯性半径估算公式见式（11），应用该估算公式计算得到的横摇惯性半径修正值曲线如图4所示。

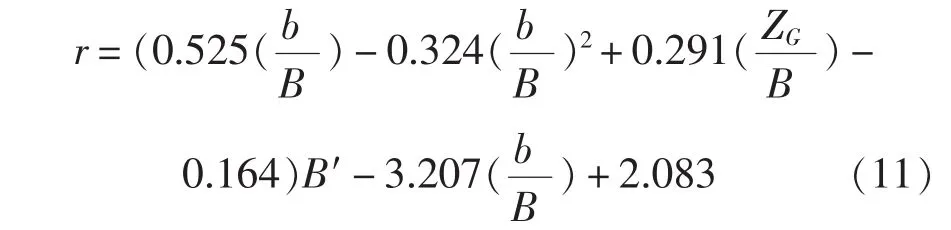
5 结 语

三体船横摇惯性半径的确定对于三体船的船模试验和耐波性预报均有着重要作用。而在船舶初步设计阶段，质量的分布是不确定的。应用本文通过计算三体梁的横向惯性半径给出三体船的横摇惯性半径估算公式，可以仅在给定主尺度和重心高的情况下估算出横摇惯性半径的值，这不仅简化了以往的计算方法，节省了计算时间，而且还有助于快速分析出横摇惯性半径对三体船性能的影响。但对于不同的船型，系数β的取值会有所不同，还需做进一步的研究。

［1］卢晓平，郦云，董祖舜.高速三体船研究综述［J］.海军工程大学学报，2005，17（2）：43-48.

［2］李培勇，裘泳铭，顾敏童.三体船横摇运动［J］.中国造船，2003，44（1）：24-29.

［3］FANG M C，CHEN T，CHEN Y.A parametric study of wave loads on trimaran ships traveling in waves［J］.Ocean Engineering，2008，35（8/9）：749-762.

［4］JIA J B，ZONG Z，SHI H Q.Model experiments of a trimaran with transom stern ［J］.International Shipbuilding Progress，2009，56（3/4）：119-133.

［5］PESMAN E，BAYRAKTAR D，TAYLAN M.Influence of damping on the roll motion of ships ［M］.Italy： Napoli（Ischia），2007.

［6］JOURNEE J M，MASSIE W W.Offshore Hydrodynamics.First Edition.［M／OL］.2001.Delft University of Technology：［2011-11-20］http： ／／www.shipmotions.nl.

［7］郭雷.斜侧体三体船阻力计算及构型研究［D］.哈尔滨：哈尔滨工程大学，2006.

［8］ZHANG J W.Roll damping characteristics of a trimaran displacement ship［J］.International Shipbuilding Progress，1999，46（448）：445-472.

［9］王波，卢晓平，姚迪.三体船操纵性计算与特性分析［J］.哈尔滨工程大学学报，2009，21（1）：47-53.

［10］王玮，王中，卢晓平.片体干扰对三体船附加质量和附加惯性矩的影响研究［J］.海军工程大学学报，2009，21（2）：83-87.

［11］李培勇，裘泳铭，顾敏童.高速三体船型概念设计研究［J］.上海交通大学学报，2004，38（11）：1885-1888.

［12］周耀华.三体船横摇阻尼及非线性运动预报方法［D］.哈尔滨：哈尔滨工程大学，2010.

［13］ZHANG J W.Design and hydrodynamic performance of trimaran displacement ships［D］.London：University College London，1997.