基于全球导航卫星系统的高轨卫星定轨理论研究及仿真实现

王 威 ,董绪荣 ,柳 丽 ,杨 洋

装备指挥技术学院,北京101416

基于全球导航卫星系统的高轨卫星定轨理论研究及仿真实现

王 威 ,董绪荣 ,柳 丽 ,杨 洋

装备指挥技术学院,北京101416

由于地基定轨系统的局限性,提出基于全球导航卫星系统(GNSS)的高轨卫星定轨方法,并设计实现了高轨卫星天基定轨仿真软件。结合高轨卫星天基定轨的特点和 GNSS的建设现状,研究卫星可见性算法和星间观测模型,综合轨道积分和Kalman滤波方法的优点,提出确定高轨卫星轨道的积分滤波方法。仿真结果表明基于GNSS完成天基定轨增加了卫星的观测量,提高了定轨精度。最后在理论研究的基础上,自主开发了集STK、Matlab和Visual C++为一体的高轨卫星天基定轨仿真平台。为北斗系统应用于高轨卫星天基定轨提供了理论上的参考依据和模拟工具。

高轨卫星定轨;Kalman滤波;星间模型;一体化仿真平台

1 引 言

高轨卫星利用卫星导航系统完成定轨,因其导航卫星可见性、观测信息少和信号微弱等问题一直是国内外该领域研究的难点。目前,国外卫星导航系统和我国北斗卫星导航系统的不断建立和完善为高轨卫星定轨提出了更大的挑战并提供了较好的机遇,如何利用丰富的导航卫星资源为高轨卫星定轨服务成为热点问题。同时,多导航系统运行、大容量信息处理和跨平台操作等问题也为建模仿真系统提出了更高的要求。本文针对以上重点问题进行研究,主要研究基于 GNSS实现高轨卫星定轨所涉及的关键理论问题,并在此基础上设计并实现了高轨卫星定轨的一体化建模仿真系统。

2 可见性算法模型

由于高轨卫星接收到的导航信号是导航卫星向地球发送的电磁波信号从地球边缘“溢出”的,而导航卫星向地球发送信号的天线波束宽度是一定的,当高轨卫星位置超过信号的天线波束宽度或者在地球的“信号阴影”里时,均接收不到导航卫星信号,其原理如图1所示,因为信号波束是非常狭窄的,可以通过角度来判断高轨卫星是否落在信号波束中。由图1知

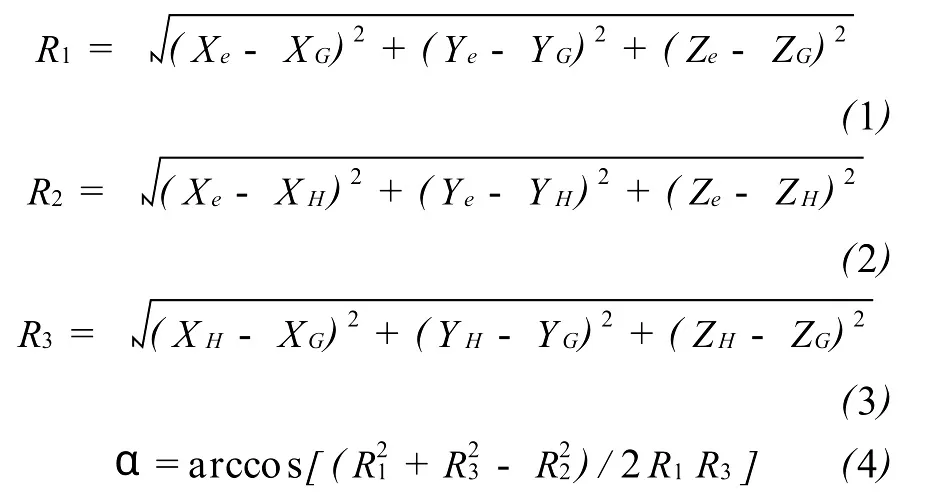
式中,(Xe,Ye,Ze)、(XG,YG,ZG)、(XH,YH,ZH)分别为地球、导航卫星、高轨卫星在J2000坐标系下的坐标。

当14.3°＜α＜19.6°时高轨卫星对该导航卫星可见,否则为不可见。

图1 高轨卫星对导航卫星可见性分析Fig.1 Visibility of the navigation satellites to GEO

由图1可知高轨卫星GEO 1、高轨卫星GEO 2、高轨卫星 GEO 3对导航卫星的可见性为:高轨卫星1的α满足14.3°＜α＜19.6°,而高轨卫星GEO 2和高轨卫星GEO 3均不满足,故对于导航卫星,高轨卫星 GEO 1可见,而高轨卫星 GEO 2、高轨卫星GEO 3均不可见。

3 星上量测方程的建立

式中,(Xj,Yj,Zj)为导航卫星的三维位置;(Xk,Yk,Zk)为高轨用户星的三维位置;bk为时钟误差引起的距离误差;N为整周模糊数。整周模糊数有很多种求解方法,这里假定为已知。

将其线性化,得

式中,(δXk,δYk,δZk)为高轨卫星项对于近似位置的改正值;为高轨用户星至导航卫星Sj的方向余弦,为高轨卫星位置近似值为高轨卫星至导航卫星Sj的距离的近似值为

将观测误差方程(6)写成矩阵形式

求解出 X后,即可按

求得高轨卫星当前时刻的位置坐标。

在上述过程中,需已知高轨卫星的概略坐标。当概略坐标较准确,并且可以观测到四颗以上导航卫星时,按上式解算即可。但若概略坐标误差较大时,由于观测误差方程线性化仅取一次项,系数阵A也是用概略坐标计算,就会使定位解算产生较大误差,此时,应采用重复解算方法,以获得准确的定位结果。观测不到四颗卫星时,该方法失效。对于高轨卫星,无法观测到四颗或更多的导航卫星,所以单纯的用载波相位来确定卫星位置的方法是不切实际的,必须通过用观测量与其他定位方式融合的方法才能正常定位解算。

4 星载导航系统天基定轨

4.1 积分滤波方法

卫星精密轨道的测定是卫星应用的前提。常见的卫星轨道测定方法有动力法和几何法。经典动力定轨法一般采用扩展弧段观测数据来估计某一历元的卫星位置和速度,通过对卫星运动方程进行积分,使不同时间的观测值联系于某一历元的卫星状态参数。这要求作用于卫星的力学模型必须十分精确,否则任何力学模型误差都将带入历元状态参数估值中。一般来说,观测量离解算历元越远,则动力模型的误差影响越大,于是积分弧度越长则力学模型误差的影响越大,即动力法定轨的轨道误差随时间的积累会越来越大。几何定轨法又称运动定轨法,该方法一般不考虑力学模型,仅依据卫星在各个离散历元的观测值估算各历元卫星的状态。对于携载接收机的卫星实现几何定轨更容易,因为不同方向的载波相位观测可以求解卫星的几何坐标,若同时利用载波相位观测,则可平滑卫星运动参数。但是,几何法对可测卫星数有严格的要求,如果某一历元时刻观测不到卫星或者可测卫星数小于四颗,则单纯的几何法定位无解,即几何法定轨受观测数据限制不能给出连续的卫星轨道。而且几何法定轨精度不高,有时不能满足一些实际要求。针对高轨卫星,若要得到连续实时的卫星轨道,则在动力轨道积分方法和 Kalman滤波法的基础上,提出一种新的定轨方法——积分滤波方法。该方法融合了轨道积分和 Kalman滤波两种定轨方法的优点,可以连续给出轨道位置的实时解。实际算例中,用此方法分别考虑了单个导航系统和多个导航系统对风云2D地球静止卫星进行定轨。

对于高轨卫星,星载导航系统积分滤波方法包括轨道积分和滤波两部分。滤波方法中包括状态方程、观测方程的建立,状态转移矩阵和导航卫星轨道的计算。由于高轨卫星上星载导航接收机的实际数据很难得到,因此,需要采用仿真试验的方法来验证提出方法的性能。仿真数据的积分滤波方法流程如图2所示。

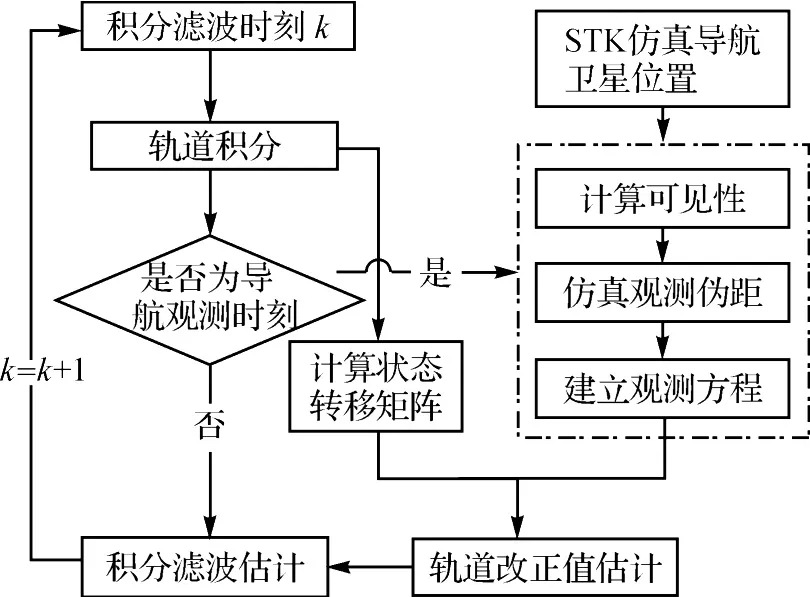
图2 星载导航系统积分滤波方法仿真流程Fig.2 Process of satellite navigation system integration filtering method simulation

4.2 模型建立

4.2.1 滤波状态方程和状态转移矩阵的求解

根据卫星的动力学特性,列出状态方程

式中,Xk为tk时刻的n维状态向量,实际中应该包括卫星的三轴位置向量、速度向量、钟差钟漂、太阳光压系数和三个补偿力模型参数,本文在仿真试验中不考虑钟差钟漂参数和太阳光压系数;Φk,k-1为 n×n维状态转移矩阵;Wk为状态噪声向量。

Wk的协方差矩阵为,一般按实际情况选取经验值。

4.2.2 观测方程及观测矩阵的求解

本文选取伪距作为观测数据,则可列出观测模型

式中,yk为k时刻的观测向量;yk0为由轨道积分得出的卫星概略位置向量;Hk为观测系数矩阵;Vk为观测噪声,其协方差矩阵R可以根据实际观测情况给出经验值。

4.2.3 最优估计解向量

下面由积分滤波估计状态参数最优值。假定已经用轨道积分法得到 k时刻的轨道积分解为Xk,J,则k时刻积分滤波估计可用下式递推得出。

以上式中带^号的为最优估计值,带～号的为预测值。

本文中考虑的摄动力有:地球引力及其摄动(考虑到8×8阶),日月引力摄动,太阳光压摄动。这样的动力学模型具有一定的误差。

4.3 仿真试验

对于星载导航系统的高轨卫星天基定轨方案,考虑基于多个导航系统的情况。

基于多个导航系统的高轨卫星天基定轨方案 ,采用 GPS、GLONASS、Galileo 和 Compass共四个导航系统(虽然后三个导航系统目前不可用,但是轨道分布及参数都基本上设计完成,可以通过仿真软件仿真导航卫星轨道)。

由于目前的 GNSS系统还没有完全建成,而且也没有高轨卫星上的实际试验数据,因此,采用仿真模拟试验验证提出的方案的性能。采用 GEO卫星FY-2D为用户卫星。用STK软件仿真四个导航星座和FY-2D卫星场景。仿真产生所有卫星一天(FY-2D卫星的周期)的轨道数据,仿真时间从2007-07-01T12:30:00.000—2007-07-02T12:29:50.000。仿真的轨道真值用 HPOP星历预报方法产生。地球模型为70×70阶的 EGM96,FY-2D卫星轨道时间间隔为10 s,导航卫星轨道间隔60 s,采用J2000坐标系,UTC时间系统。

计算 GNSS卫星和FY-2D卫星之间的距离,加入随机误差作为模拟的伪距观测值,加入的随机误差服从分布N(0,0.9 m)。STK产生的FY-2D卫星的位置速度向量作为待估计参数的真值。初始值由前一个时刻真值加入已知误差生成。用提出的积分滤波方法计算FY-2D卫星的轨道解,与STK软件给出的真值相减作为误差。

方案的仿真结果如图3所示。

图3 定轨误差曲线图Fig.3 Orbit determination error

从仿真结果可以看出,通过综合多个 GNSS系统信息的方法可以较好地增加观测量,降低定轨误差,方案的精度较高,在3 m以下,取得了很好的效果。

5 星载导航系统天基定轨建模仿真系统

基于以上研究,笔者设计并完成了高轨卫星天基定轨建模仿真系统,仿真系统软件首先借助STK软件模拟仿真多种星座系统,并实现了基本的星座控制功能,最后产生卫星数据,利用Matlab仿真软件进行高轨卫星定轨模型的仿真,对定轨方法实现了原理验证。软件利用Visual C++进行系统集成,同时利用Matcom动态链接库实现了在Visual C++中兼容Matlab的仿真,实现了集 STK、Matlab、Visual C++为一体的高轨卫星定轨建模仿真系统,提高了建模速度和仿真效率。

图4 系统数据流程Fig.4 Data flow of the system

系统数据流程如图4所示。主要功能为:

(1)能够对用户星以及多种导航星座轨道进行仿真,计算任一时刻各类卫星的位置,并实现2D和3D场景中的多功能演示。

(2)能够实现用户星对导航星座卫星的可见性进行分析,并完成该时刻用户星和导航卫星位置、速度及位置坐标、载波相位观测值等数据的生成及存储。

(3)能够对任意时刻高轨卫星天基定轨状况效果仿真,显示星下点轨迹和空间位置,并同时获得导航数据。

(4)能够依据导航数据,采用多种定轨方法进行原理验证,并显示定轨精度和可见性等演示结果。系统运行效果如图5所示。

图5 基于 GNSS的高轨卫星天基定轨建模仿真系统运行效果图Fig.5 Orbit determination for geostationary satellite based on GNSS

6 结束语

本文研究了基于 GNSS的高轨卫星定轨方法,采用积分滤波法实现了高轨卫星的高精度定轨。设计了高轨卫星定轨建模仿真系统,实现了多仿真系统并行操作、仿真环境快速建立、高效能仿真运算等功能。研究内容具有理论和现实意义。

[1] GERLACHL C,SNEEUW N,VISSER P,et al.CHAMP Gravity Field Recovery Using the Energy Balance Approach[J].Advances in Geosciences,2003(1):73-80.

[2] DUNN C,BERTIGER W.The Instrument on NASA′s GRACE Mission:Augmentationof GPS to Achieve Unprecedented Gravity Field Measurements[C]∥Proceedings of ION GPS.Portland:ION,2002:724-730.

[3] SVEHLA D,ROTHACHER M.Kinematic and Reduceddynamic Precise Orbit Determination of Low Earth Orbiters[J].Advances in Geosciences,2003(1):47-56.

[4] LIU Haiying,WNA G Huinan.Orbit Determination of Satellite on the Middle/High Earth Orbit Based on GPS[J].Chinese Journal of Space Science,2005,25(4):293-297.(刘海颖,王惠南.基于 GPS的中、高轨道航天器定轨研究[J].空间科学学报,2005,25(4):293-297.)

[5] YU Shuochun,GAO Yijun.GPS Based Autonomous Orbit Determination Research for Geostationary Satellites[J].Aerospace Control,2005(4):65-69.(俞朔春,高益军.基于GPS的静止轨道卫星自主定轨技术研究[J].航天控制,2005(4):65-69.)

[6] ZHAO Qile,LIU Jingnan,GE Maorong,et al.Precision Orbit Determination of CHAMP Satellite with cm-level Accuracy[J]. GeomaticsAnd Information Science of Wuhan University,2006,31(10):84-87.(赵齐乐,刘经南,葛茂荣,等.CHAMP卫星cm级精密定轨[J].武汉大学学报:信息科学版,2006,31(10):84-87.)

[7] WANG Feixing,LU Biying,ZHOU Zhimin.Research on Autonomous Navigation Method Using TDRSS[J].Space Electronic Technology,2005(3):8-13.(王飞行,陆必应,周智敏.利用TDRSS自主导航定位的方法研究[J].空间电子技术,2005(3):8-13.)

[8] QIN Honglei,LIANG Minmin.Research on Positioning of High Earth Orbital Satellite Using GNSS[J].Chinese Journal of Space Science,2008,28(4):316-320.(秦红磊,梁敏敏.基于GNSS的高轨卫星定位技术研究[J].空间科学学报,2008,28(4):316-320.)

[9] ANDRES R B-M.In-orbit Autonomous Position Determination of SatellitesUsing Sparsely Distributed GNSS Measurements for GTO,GEO and Higher Altitudes[D].Cranfileld:School of Engineering,Cranfield University,2010.

[10] LI Qiao,LIM Samsung,RIZOS Chris,et al.A Multiple GNSS-based Orbit Determination Algorithm for Geostationary Satellites[C]∥Proceeding of IGNSS Symposium 2009,Queensland:IGNSS,2009.

[11] LUTHCKE S B,ZELENSKY N P,et al.The 1-centimeter Orbit:Jason-1 Precision Orbit Determination Using GPS,SLR,DORIS,and Altimeter Data[J].Marine Geodesy,2003(26):399-421.

(责任编辑:杨洪泉)

Research and Simulation of Orbit Determination for Geostationary Satellite Based on GNSS-

WANG Wei,DONG Xurong,LIU Li,YANG Yang
Academy of Equipment Command&Technology,Beijing 101416,China

As the limitations of ground orbit system,this paper presents a method of orbit determination of GEO satellite based on GNSS,and designs an orbit determination of GEO satellite software.Combination of orbit determination of GEO satellite characteristics and construction of GNSS,the satellite visibility algorithms and inter-satellite observation model are discussed,integral filter method is proposed to determine the orbit of geostationary satellite to make use of the advantage of orbit integral and Kalman filter method.Simulation results show that orbit determination of GEO satellite based on GNSS can increase the satellite observations and improve the accuracy of orbit determination.Finally,the paper develops a space-based orbit determination of GEO satellite simulation platform with STK,Matlab and Visual C++.The outcomes of this paper will provide theoretical reference and ideal simulation tool for the application of Compass on orbit determination of GEO satellite.

orbit determination of GEO satellite;Kalman filter;satellites observation model;simulation platform

WANG Wei(1984—),male,PhD candidate,majors in GNSS positioning theory and application.

P228

:A

1001-1595(2011)S-0006-05

2011-01-28

修回日期:2011-03-25

王威(1984—),男,博士生,研究方向为卫星导航定位理论与应用。