基于高斯过程的精密卫星钟差加密

刘 冬,张清华,2

1.西安测绘研究所,陕西西安 710054;2.信息工程大学测绘学院,河南郑州450052

基于高斯过程的精密卫星钟差加密

刘 冬1,张清华1,2

1.西安测绘研究所,陕西西安 710054;2.信息工程大学测绘学院,河南郑州450052

将高斯过程方法应用到精密卫星钟差加密中,通过选择合适的核函数,将5 min间隔的钟差数据插值到30 s间隔。将结果与IGS提供的30 s精密钟差数据和四阶多项式拟合插值方法得到的结果进行比较,结果表明,高斯过程方法具有较高的加密精度,适用于 GPS所有在轨卫星的原子钟钟差的加密,达到厘米级精度。

精密钟差;加密;高斯过程;回归

1 引 言

GPS精密单点定位技术不能用组差的方式来消除卫星钟差,而广播星历中的卫星钟差精度也仅为7 ns,无法满足精密单点定位的要求。通常采用IGS提供的钟差产品,将15 min或5 min的精密卫星钟差加密到用户所需的采样间隔。由于实际数据采样率会更高,所以必须采用估计或内插的方法得到高采样率的卫星钟差。因此,对精密星历进行内插或拟合就成为 GPS精密数据处理等实际应用中的重要工作。

目前,国内外较常用的加密方法是Lagrange多项式插值、Newton多项式插值、Hermite插值、样条函数插值、切比雪夫多项式插值、三角函数插值等[1-2]。

本文采用高斯过程回归方法进行精密钟差加密,通过选择合适的协方差函数,将 IGS提供的5 min间隔的精密钟差数据插值到30 s间隔,试验结果表明,该方法具有较高的加密精度,且对所有的卫星原子钟都有较强的适用性。

2 高斯过程回归

高斯过程回归是近年来由统计学理论发展来的一种全新学习机,它将函数视为变量,由训练数据和贝叶斯估计理论得到关于函数的后验概率估计,达到对函数学习的目的。它对处理高维数、非线性复杂分类和回归问题具有很好的适应性,且泛化能力强,与人工神经网络、支持向量机相比,有较容易实现的特点。

2.1 高斯过程

随机过程可以定义为在某个概率空间上的一簇随机变量。高斯过程是一种重要的随机过程,是对高斯分布的推广。如果高斯分布是描述向量的分布情况,那么可以将高斯过程理解为是描述函数的分布情况。

高斯过程又称正态随机过程,其任意有限变量集合都有着联合高斯分布的特性,即对于任意整数 n≥1及任意的变量 x1,x2,x3,…,xn,与其对应的函数 f(x1),f(x2),f(x3),…,f(xn)的联合概率分布服从n维高斯分布。高斯过程的全部统计特征完全由它的均值 m(x)和核函数 k(x,x′)来确定,一般记为 f(x)～GPf(m(x),k(x,x′))。核函数是任意一对输入的随机变量 x和 x′的协方差函数。高斯过程的核函数必须是半正函数。与神经网络类似,通常需要通过训练数据集来确定核函数的超参数,具体训练方法见参考文献[3—4]。

假设有 N个观测数据的训练集D={(x1,y1),(x2,y2),(x3,y3),…,(xN,yN)},xi∈Rnx,是nx维输入矢量,yi∈R是相应的输出标量,令 X=[x1x2x3… xN],y=[y1y2y3…yN]。应用内积空间中的重构核希尔伯特空间(reproducing kernel Hilbert space,RKHS)来描述输入输出的关系,即考虑映射 φ:Rnx|→H,由此可得

一般情况下,认为 b=0(可以采用剔除均值的方法得到)。对于给定的训练数据集

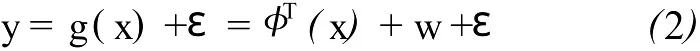
如果假定w的先验概率为N(0,I),其中ε是独立的随机变量,服从均值为0,方差为δ2εI的高斯分布,那么 y是高斯过程。

令 k(xi,xj)=〈φ(xi),φ(xj)〉,则

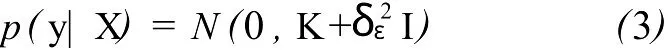
式中,Kij=k(xi,xj)。

2.2 高斯过程预测

高斯过程预测是指对任意的测试输入 x＊,给出其函数值的预测值 g(x＊),写成概率分布函数的形式,即条件分布p(g(x＊)|x＊,X,y)。根据公式(3)可以将训练输出 y和预测值g(x＊)写成联合分布,即

式中,k＊=K(X,x＊),k＊＊=k(x＊,x＊)。根据联合分布,可以很容易得到 g(x＊)的条件分布函数

3 基于高斯过程的钟差加密

导航卫星中在外部空间受到极其复杂的环境影响,使得钟差数据具有一定的不稳定性,又没有具体的规律可循,因此可以通过高斯过程回归的学习能力对钟差数据来进行拟合,进而进行加密。在学习过程中,协方差函数的选择非常重要。

在考虑时变钟漂参数时,国外常用的频漂模型是对数模型和指数模型。同时在对 GPS卫星钟特性分析和实际钟差数据试验的基础上,选取Matern协方差函数作为核函数[3],其表达式如下

式中,v,l是正参数;Kv(·)为修正的Bessel函数;d(x,x＊)为距离函数。在实际应用中,核函数的参数选择为v=3/2,l=1。选择了各向同性函数作为距离函数,即

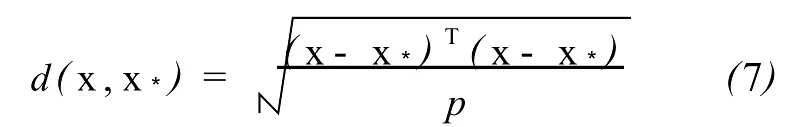
式中,p为比例系数。最终采用的核函数为

式中,s为信号方差,s和p是该核函数的超参数。如果将距离当作变量,显然,该核函数可以看成是一个指数函数和一阶多项式的乘积。

4 算例与分析

为了分析与比较几种钟差加密方法的精度,采用IGS提供的2009-08-21的间隔为30 s的钟差数据(igs15455.clk_30s)。在其中读取卫星的钟差,其采样间隔为30 s,将其作为真值,再从中挑选间隔为5 min的数据作为节点,分别用多项式拟合法(Polyfit),高斯过程回归算法(GP)进行加密,并将加密结果与真值进行比较分析,其方案如下:

(1)用四阶多项式拟合和高斯过程回归算法来对 PRN32卫星在一天内的数据进行加密,并对加密的结果进行统计分析。

(2)采用四阶多项式和高斯过程回归算法对不同类型的卫星原子钟的钟差加密进行加密,对结果进行统计分析。

4.1 PRN32卫星的钟差加密

采用四阶多项式和高斯过程方法对PRN32卫星钟差进行加密,其24小时的拟合结果如图1所示,图2给出了局部放大的拟合结果,图3是钟差拟合残差(与真实钟差的差),每个历元为30 s。由图3可以看出,采用 GP方法得到的精密钟差与真实钟差的偏差非常小,并且在24小时中都非常稳定,而采用四阶多项式方法得到的钟差不仅加密误差加大,而且具有明显震荡。表1给出采用不同方法得到的拟合均方误差(RMS),显然,采用 GP方法进行钟差加密要比四阶多项式方法钟差加密的精度提高很多(相差一个数量级),达到了27 ps,等效距离误差约0.81 cm。

图1 钟差拟合结果曲线(PRN32卫星)Fig.1 Clock error fitting(PRN32)

图2 钟差拟合结果局部放大曲线(PRN32卫星)Fig.2 Clock error fitting selective enlargement(PRN32)

表1 加密精度比较(PRN02卫星)Tab.1 Comparison of densification precision(PRN32)/ns

图3 钟差拟合残差曲线(PRN32卫星)Fig.3 Clock error fitting residual(PRN32)

4.2 不同类型卫星钟的钟差加密

为了验证 GP方法钟差加密的适用性,利用IGS提供的2009-08-21所有卫星钟差数据进行试验。图4是采用四阶多项式方法对不同卫星钟中进行钟差加密精度(均方误差)。图5是采用GP方法对不同卫星钟中进行钟差加密精度(均方误差)。表2是两种方法对不同卫星钟加密精度的统计结果。通过对比,采用 GP方法对不同卫星钟的钟差进行加密,都可以得到较高的插值精度,且不同卫星钟的拟合误差量级基本相同;四阶多项式方法对 GPS中BlockⅡA卫星的Cs钟的拟合误差较大。分析结果表明:采用四阶多项式方法加密钟差,对于 GPS中BlockⅡA卫星的Cs钟和Rb钟,钟差误差达到了分米级;GP方法对于所有的 GPS卫星钟加密都有非常好的适用性,加密精度都可达到厘米级。

图4 多项式拟合的加密精度Fig.4 Densification precision of polynomial fitting

图5 高斯过程回归加密精度Fig.5 Densification precision of Gaussian processregression

表2 不同卫星原子钟加密精度比较Tab.2 Comparison of densification precision for different satellite atomic clocks /ns

5 结束语

钟差加密是 GPS数据处理中重要而经常性的工作,应用高斯过程方法对 GPS卫星钟的钟差进行加密,通过与四阶多项式钟差加密方法的精度对比,得出以下结论:①采用 GP方法对 GPS卫星钟的钟差进行加密具有较高的插值精度高,残差稳定;②GP方法钟差加密对于所有的 GPS卫星钟都有普遍的适用性。

[1] HAN Baomin.Densification Methods of GPS Satellite Clock Errors and Their Impact on Orbit Determination Precision of LEOs[J].Geomatics and Information Science of Wuhan University,2006,31(12):1076-1079.(韩保民.精密卫星钟差加密方法及其对星载 GPS低轨卫星定轨精度影响[J].武汉大学学报:信息科学版,2006,31(12):1076-1079.)

[2] HONG Ying,OU Jikun,PENG Bibo.Three Interpolation Methods for Precise Ephemeris and Clock Offset of GPS Satellite[J].Geomatics and Information Science of Wuhan University,2006,31(6):516-518.(洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报:信息科学版,2006,31(6):516-518.)

[3] RASMUSSEN C E,WILLIAMS C K I.Gaussian Processes for Machine Learning[M].Berlin:Springer,2006.

[4] RASMUSSEN C.Evaluation of Gaussian Processes and Other Methods for Non-linear Regression[D].Toronto:University of Toronto,1996.

(责任编辑:宋启凡)

Densification of Precise Satellite Clock Errors Based on Gaussian Processes

LIU Dong1,ZHANG Qinghua1,2
1.Xi’an Institute of Surveying and Mapping,Xi’an 710054,China;2.Institute of Surveying and Mapping,Information and Engineer U-niversity,Zhengzhou 450052,China

The Gaussian processes(GP)method is used to densify the 5 min interval clock errors to 30 s interval with a suitable kernel function.The densification results are compared with the IGS data and the densified clock errors using the four order polynomial interpolation method.The results indicate that the GP method can provide high densification precision and is applicable to densify the clock errors of all GPS on-board atom clocks.The accuracy is up to the centimeter level.

precise clock errors;densification;Gaussian processes;regression

LIU Dong(1977—),male,PhD,majors in is satellite navigation and nonlinear signal processing.

P135

:A

1001-1595(2011)S-0059-04

2011-01-31

修回日期:2011-03-19

刘冬(1977—),男,博士,研究方向为卫星导航与非线性信号处理。

E-mail:ld_yzy@yahoo.com.cn