基于AHP的农村教师流动主要因素分析
○孙 炎 尚 娜 何 洋
(云南农业大学经济管理学院 云南 昆明 650201)
基于AHP的农村教师流动主要因素分析
○孙 炎 尚 娜 何 洋
(云南农业大学经济管理学院 云南 昆明 650201)
在农村教师的流动过程中,目前存在农村教师的单向外流现象,严重削弱了农村教育资源的发展,对教育公平起到一定的阻碍作用。本文运用层次分析法对农村教师的流动因素进行分析,找出制约农村教师流动的关键因素,并提出了相应的解决对策。
AHP法 农村教师 流动因素
人才流动是指人才在地区、行业、岗位等方面的变动。目前我国农村地区教师的单向外流现象严重削弱了农村中小学的师资力量,成为制约教育均衡发展、实现教育公平的瓶颈。本文主要运用层次分析法,从实证分析角度对制约农村教师流动的因素进行分析,对解决农村教师单向外流现象提出有针对性的合理建议。
一、AHP模型
层次分析法(Analytic Hierarchy Process,AHP)于 20世纪70年代中期由美国运筹学家塞蒂(T.L.Saaty)正式提出,它作为一种多层次权重分析决策法,将决策者的思维过程系统化、模型化、数量化。其最终将各方法或者措施排出优劣次序,用来解决结构较为复杂、准则较多且不易量化的决策问题。AHP在决策分析过程中主要有以下几个步骤。
1、构建问题的层次结构模型
建立层次结构,把问题分解为若干层次。第一层为总目标,中间层可根据问题的性质分成准则层或者部门层等,最底层一般为方案层或者措施层。
2、构造成对比较矩阵
假设当前层次上的因素为P1,P2,P3,…Pn,相关的上一层因素为C(可以不止一个),则可针对因素C,对所有因素P1,P2,P3,…Pn进行两两比较,得到数值aij,其定义和解释见表1。
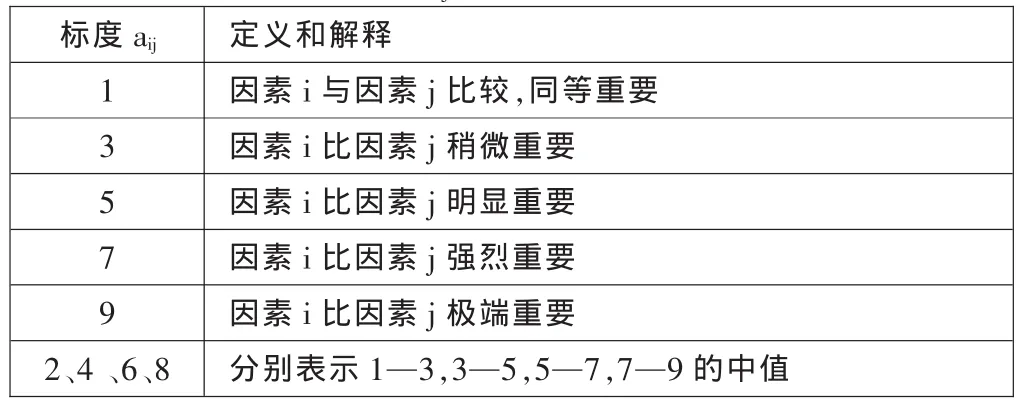
表1 aij的定义和解释
3、计算层次单排列权向量并做一致性检验
记P的最大特征根为λmax,属于λmax的标准化特征向量为 w=(w1,…wn)T,可用和积法计算得到 λmax和 w。在得到判断矩阵P时,有时免不了会出现判断上的不一致性,因而需要利用一致性指标来进行检验。作为度量判断矩阵偏离一致性的指标,可以用CI=(λmax-n)/(n-1)来检查决策者判断思维的一致性。为了度量不同判断矩阵是否具有满意的一致性,还需要利用判断矩阵的平均随机一致性指针RI。对于1到9阶的判断矩阵,RI的值分别如表2。

表2 1到9阶的判断矩阵中RI的值
结果得到随机性一致性比率CR=CI/RI,通常要求CR≤0.1,此时可以认为判断矩阵具有满意的一致性,否则需要对判断矩阵进行调整。
4、计算层次总排列各因素权值并决策
利用同一层次中所有层次单排序的结果,就可以计算针对上一层次而言本层次所有因素重要性的权值,这就是层次总排序。层次总排序需要从上到下逐层顺序进行,对于最高层下面的第二层,其层次单排序即为总排序。最后根据层次总排列各因素权值的相关顺序,我们可以作出所需要的决策。
二、AHP在农村教师流动过程中的应用
1、建立层次结构模型
农村教师流动决策问题可分解为三个层次:第一层是目标层O,即制约农村教师流动因素;中间层是准则层C,本文以政策因素C1、经济因素C2、管理因素C3、个人因素C4共四个准则为决策准则;下层是指标层P,即对经济因素和个人因素的具体分解。其层次结构如图1所示。
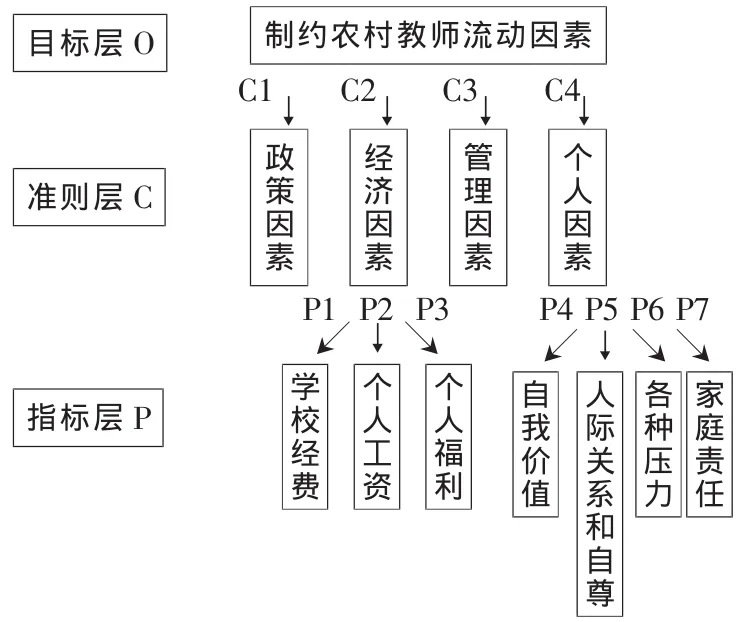
图1 制约农村教师流动因素结构图
2、构造成对比较矩阵
采用表1的1—9标度法进行成对比较,同时根据调研实际情况参考专家意见确定各种因素之间的相对重要程度,进行打分,构造出各个层次中的所有成对比较矩阵(C1和C3为单因素,因此不用给出成对比较矩阵)。
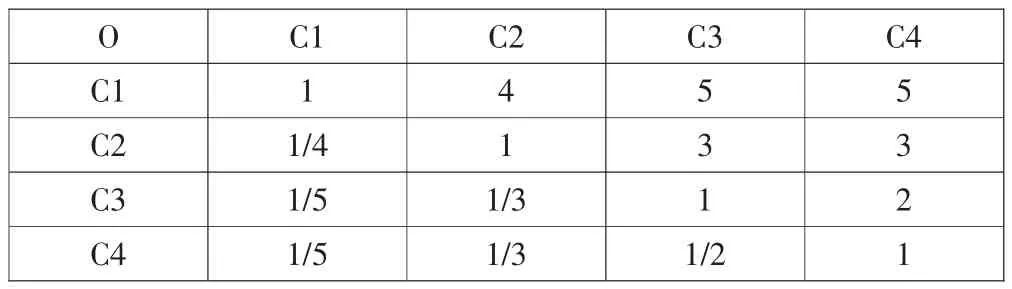
表3 目标层O与准则层C构成的成对比较矩阵J1

表4 C2与P构成的成对比较矩阵J2
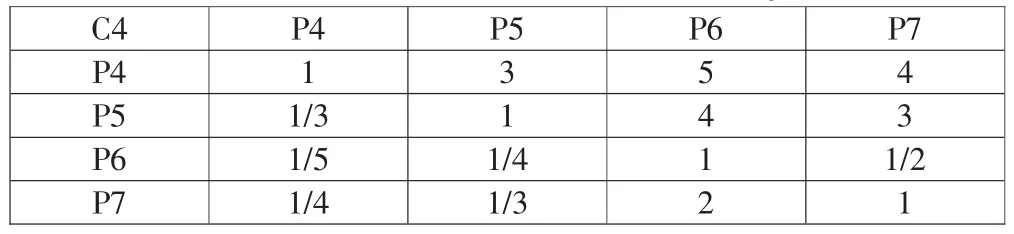
表5 C4和P构成的成对比较矩阵J3
3、层次单排列
用和积法计算矩阵J1的特征根和特征向量:

所以 PW=(2.478,0.966,0.470,0.330)T。
准则层各因素构成的比较矩阵的最大特征根λmax1=4.16,相应的权向量为 W1=(0.573,0.299,0.117,0.081)T。
进行J1矩阵的一致性检验,计算其一致性指标CI1=0.053。
查随机一致性指标RI的表2得RI1=0.89,所以一致性比率为:CR1=CI1/RI1=0.053/0.89=0.06<0.1,这说明矩阵J1是一致性矩阵,所以可选择W1作为权向量。
同理,可以求得矩阵J2的最大特征根λmax2=3.025,相应的权向量为 W2=(0.118,0.681,0.201)T。
进行J2矩阵的一致性检验,计算其一致性指标CI2=0.012。
查随机一致性指标RI2的表2得RI2=0.58,所以一致性比率为:CR2=CI2/RI2=0.012/0.58=0.024<0.1,这说明矩阵J2是一致性矩阵,所以可选择W2作为权向量。
矩阵J3的最大特征根λmax3=4.115,相应的权向量为W3=(0.526,0.273,0.077,0.124)T。
进行J3矩阵的一致性检验,计算其一致性指标CI2=0.038。
查随机一致性指标RI3的表2得RI3=0.89,所以一致性比率为:CR3=CI3/RI3=0.038/0.89=0.043<0.1,这说明矩阵J3是一致性矩阵,所以可选择W3作为权向量。
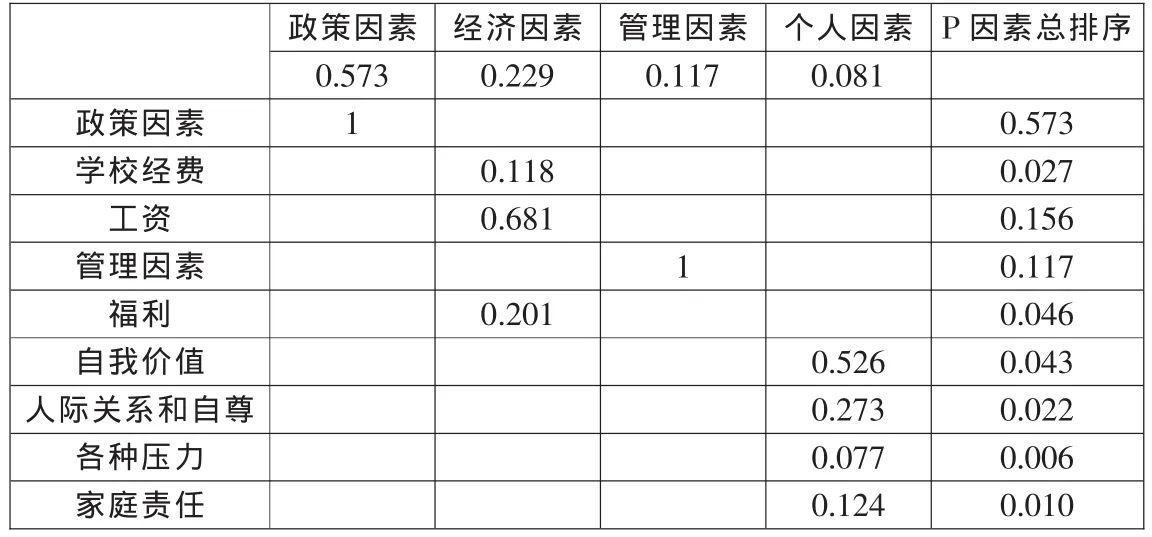
表6 制约农村教师流动因素的层次总排列
4、层次总排列
在制约农村教师流动因素中,利用经济因素和个人因素指标层的单排列结果,就可以计算出针对准则层而言,指标层所有因素重要性权值的结果(计算结果见表6)。
从上述结果可以看出,制约农村教师流动的因素中,政策因素是关键因素,这里政策因素包括农村教育政策和政府政策;经济因素次之;个人因素所占比重最小。
另外,从所有因素的层次总排列可以看出,政策因素还是成为制约农村教师流动的最关键因素,工资成为第二关键因素。其余相关因素的顺序依次是:管理因素、福利、自我价值、学校经费、人际关系和自尊、家庭责任、各种压力。
三、缓解农村教师流动的对策
1、政府对教育的重视与支持
政策因素是制约农村教师流动的关键因素,因此政府在制定农村教育政策时,要考虑到农村现存制度格局,真正实现农村教师流动的均衡发展。近些年来,尽管国家和当地政府在努力纠正城乡教育之间的偏差,但是由于多年问题的积淀而使效果不明显。只有当政策制定与实际情况相结合的时候,其过程和结果才会令人满意。
2、建立农村教师补偿机制
工资是制约农村教师流动的第二关键因素。农村教师工资低成为许多农村教师单向外流的直接原因,因此国家应该建立一套针对农村教师流动的补偿机制。这里的补偿机制不仅包括对农村教师工资的补偿,还需要结合对农村教师的评估、培训和开发过程进行整合与调整,达到强化农村教师的教学素质与教学质量的目的。
3、健全完善农村学校管理制度
在调查中显示,一些有能力的农村教师一旦因为教学工作表现突出,就被提拔做行政工作,他们就少教课或者不教课。这实际是在过分夸大权力在教学过程中的作用。此外,当农村教师想通过自己的能力来实现利益目标时,如果学校管理的各项考核不够公正,不向骨干教师倾斜,那么就会造成农村教师的心理失衡,引起教师们为寻找平衡而流动。因此,农村学校的管理应该更加公平、民主。
[1]胡运权:运筹学教程[M].北京:清华大学出版社,2005.
[2]汪洁:管理学基础[M].北京:清华大学出版社,2009.
[3]杨景祥、苑健斌:层次分析法在供应链构建中的应用[J].中国商贸,2010(3).
[4]兰继斌、刘雁、王中兴:层次分析法方案排序向量的研究[J].重庆工学院学报,2006,21(1).
[5]高志杰:基于AHP的黑龙江省中小企业技术创新能力模糊综合评价[J].生态经济,2010(8).
[6]王瑞珍:从教育公平原则看义务教育城乡差距[J].中共福建省委党校学报,2008(5).
[7]陈潭:公共政策案例分析[M].北京:社会科学文献出版社,2008.
(责任编辑:胡婉君)

