遗传模拟支持向量机在居民消费价格指数预测中的应用
○罗芳琼
(柳州师范高等专科学校 广西 柳州 545004)
遗传模拟支持向量机在居民消费价格指数预测中的应用
○罗芳琼
(柳州师范高等专科学校 广西 柳州 545004)
为了能够准确地对我国居民消费指数进行预测,本文深入研究了支持向量机在居民消费价格指数中的预测,首先阐述了最小二乘支持向量机的基本理论,接着提出了遗传模拟退火算法,最后进行实例研究,结果表明该方法具有较高的预测精度。
支持向量机 居民消费价格指数 预测
居民消费指数可以在国际上通用,该数据指标的意义在于能够反映通货紧缩或膨胀的程度,可以为制定价格政策、工资政策、货币政策以及居民消费政策提供有利的理论依据,而且有利于对国民经济进行核算。
支持向量机具有结构简单和泛化能力强的优势。标准支持向量机算法逐渐演变出了最小二乘支持向量机算法,它的两个调整参数分别为核宽度σ和正则化参数λ,最小二乘支持向量机的训练和泛化能力完全由这两个参数所决定,但是这两个调整参数的选择是比较困难的,没有一种有效的选择方法,通常情况下是根据经验来选择的,一方面费时费力,另一方面预测效果精度不高。因此,应该找出一种优化的调整参数确定手段。很多的模式分类中,需要抽取大量的潜在特征,所以,必须在所抽取的潜在特征中找出明显的子特征,然后依据子特征开始分类。因此,不同的特征都应该明确其对分类的贡献性,以这种方法发现特征子集的方法属于优化组合问题。
一、最小二乘支持向量机
Suykens和Vandewalle首先提出了最小二乘支持向量机的概念,其表达式如下:
设(xi,yi),i=1,2,…,n为非线性系统的输入输出样本数据集合,其中 xi∈,yi∈,d 表示变量的维数。利用最小二乘支持向量机将这些数据样本构成非线性系统模型,主要步骤如下。
首先,利用非线性变换x→φ(x)把原来输入至系统的数据样本点xi转换到另外一个高维的希而伯特空间,原来的问题就被转换成了在高维空间的线性问题。
其次,建立高维空间的线性模型。在高维特征空间中对应于原始输入空间的样本点xi的分类函数可以用如下方程来表示:

其中,<,>用来表示两个向量的内积,φ代表权重向量,φ(x)代表非线性映射函数,α表示阈值。按照Vapnik提出的VC维方法以及结构风险最小化理论,同时利用最小二乘支持向量机完成系统的优化,因此,式(1)中的函数f(x)应该满足以下条件:


其中,λ代表正则化参数。
将拉格朗日算子引入公式(2)和公式(3),可得:
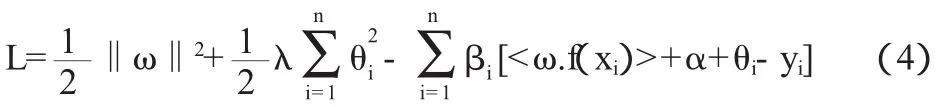
其中:βi≥0代表拉格朗日算子。求出公式(4)的驻点,令ω、α、θi、βi、的一阶偏导数为 0,可得:
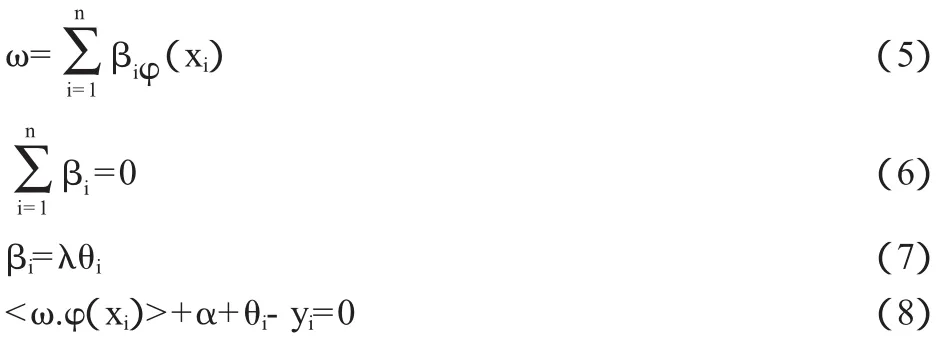
求解方程(5)-(8)能够将ω和θ这两个参数去掉,进而能够得到:

利用最小二乘法求解方程(9),因此,在训练速度上,最小二乘法支持向量机比传统的支持向量机具有更快的速度,=[β1,β2,…βn]T和 α 能够利用最小二乘法计算得到,从而可以获得非线性的系统模型:
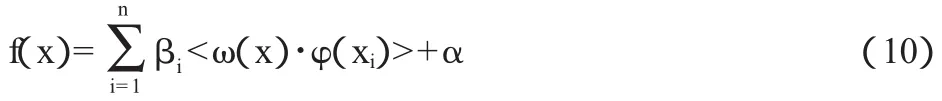
相应的核函数非线性系统模型可以表示为如下的形式:

二、改进的遗传模拟退火算法
1、基于嵌套混合策略的RCPSPGSA算法框架
对于数控机床的故障诊断问题来说,混合策略通常分为三类,分别是嵌入式策略、两阶段策略以及嵌套策略。对于嵌入式策略,将把他元启发手段看作进化功能。两阶段策略利用其他元启发方法在第一阶段初始化GA的初始种群,然后GA以其传统方式在第二阶段工作。在嵌套策略中,其他元启发方法被嵌套在GA中以提高GA的局部搜索能力。在改进的遗传模拟退火算法中选择了嵌套策略。改进的遗传模拟退火算法的操作流程如下所示。
(1)进行参数的初始设置。
(2)产生初始种群。
(3)评估初始种群,并令Best等于当前最优解,k=0。
(4)如果终止条件(进化迭代次数达到预设值或最优解持续Ⅳ次迭代没有发生改变)满足,转到步骤11。
(5)进行选择操作。
(6)交叉操作。
(7)进行变异操作。
(8)形成具有PopSize(种群个体数量)个个体的临时下代种群,该种群中个体将作为SA的初始解。计算该种群的最优解,并更新Best。
(9)使用给定的步长SA提高临时下代种群中的每个个体的能力,新个体以概率 min[1,exp(-△/tk]来接受,接着更新Best。
(10)令 k=k+1,tk=εtk+1,转步骤 4(ε 是退温速率)。
(11)输出最优解 Best。
2、编码方式和解码规则
(1)参数组合。利用遗传模拟退火算法对支持向量机的调整参数进行优化,对于最小二乘支持向量机有两个调整参数,一个是核宽度σ,另一个是正则化参数λ。不同的特征与两个值相对应,一个是0,另外一个是1。0表示不取该特征,1表示确认该特征。因此,可行解的可以表示为(λ,σ,F1,F2,…Fn)。
(2)分类的正确率。利用十折交叉验证的方法把数据集划分为十份,循环地将其中一份数据集看作测试数据,其余九份看作训练样本进行试验,最后得到十次诊断的准确率平均值,对分类准确率进行分类。
(3)借助遗传变异的思想。形成新的参数组合的目的是能够使形成的参数在参数组合空间中充满。将遗传算法和模拟退火算法进行混合,能够提高模拟退火算法的诊断能力,达到形成新的可行参数组合。
三、居民价格消费指数的预测
为了验证该方法的有效性和实用性,选择2004年到2009年的居民消费价格指数的数据作为最小二乘支持向量机的输入样本,将最小二乘支持向量机作为居民价格消费指数预测的分类器导入到遗传模拟退火算法中。首先,利用该算法训练样本数据,从而可以得到最佳的支持向量机参数以及最优的特征组合;接着,利用最小二乘支持向量机对居民价格消费指数进行预测。民消费价格指数进行仿真,仿真结果如表2所示。

表1 2005—2010年居民消费价格指数表
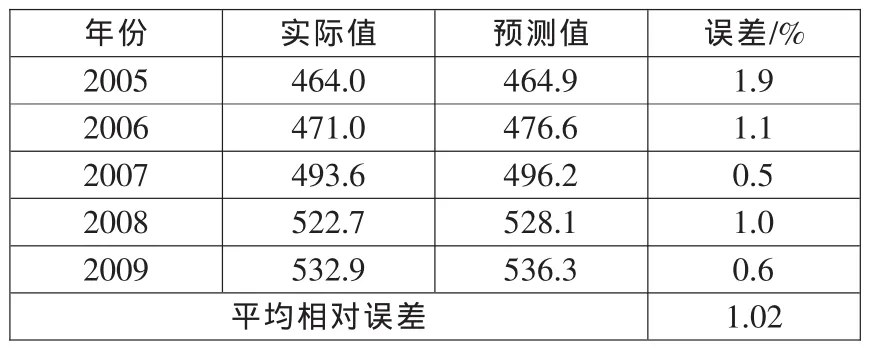
表2 基于遗传模拟退火支持向量机的居民消费价格指数仿真结果
利用遗传模拟退火支持向量机对我国2005—2009年的居
通过表2可以得出以下结论,利用遗传模拟退火支持向量机可以准确地预测居民消费价格指数。相应的遗传模拟退火支持向量机对居民消费价格指数进行预测的误差曲线如图1所示,支持向量机过750次迭代后平均误差降低到0.12456,表明该方法具有良好的预测能力。
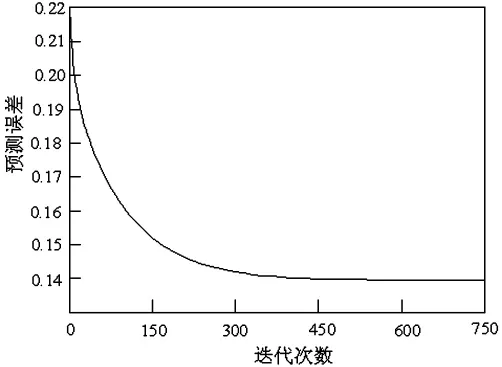
图1 支持向量机预测居民消费价格指数的误差曲线
接着,利用遗传模拟退火支持向量机对2010—2015年我国居民消费价格指数进行预测,预测结果见表3。从而,可以根据预测结果制定货币政策、工资政策等。
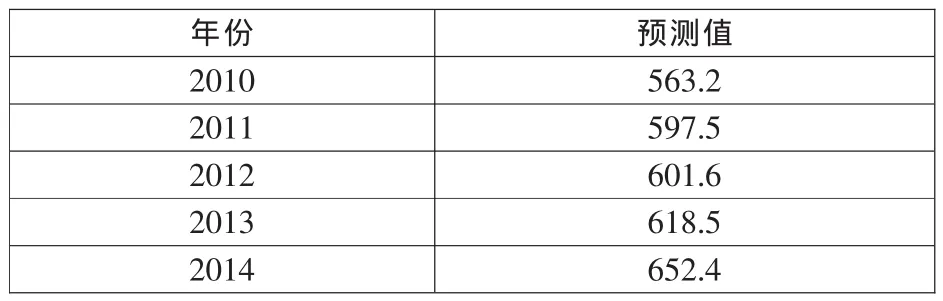
表3 2010—2015年居民消费价格指数预测结果
参数的选择对遗传模拟退火算法支持向量机的预测能力影响比较大,将遗传模拟退火算法的支持向量机和网格搜索法进行对比,其性能优于网格搜索法,比较结果见表4。

表4 遗传模拟退火算法的支持向量机与网络搜索法的比较
四、结束语
利用遗传模拟退火算法对支持向量机进行参数的选择和特征的优化,并且将该方法应用于居民消费价格指数的预测中去,利用2005年到2010年的居民消费价格指数的数据对2011年我国居民价格消费指数进行了预测,结果表明遗传模拟退火算法的支持向量机具有较好的预测准确性,能够成功地排除不利的干扰。
(注:基金项目:基于支持向量机的机器学习方法研究(NO.LSZ2009B005)。 )
[1]曹捍东:基于VAR模型的中国CPI分析[J].统计与决策,2006(14).
[2]张海波、徐慧:我国CPI波动的影响因素分析[J].统计与决策,2009(19).
[3]王计生、喻俊馨、黄惟公:小波包分析和支持向量机在刀具故障诊断中的应用[J].振动、测试与诊断,2008,28(3).
(责任编辑:李文斐)

