Temperature control and cracking prevention in coastal thin-wall concrete structures

Li-xia GUO*, Xiao-hong BAI, Ling ZHONG, Sheng QIANG

1. Faculty of Water Conservancy Engineering, North China University of Water Conservancy and Electric Power,Zhengzhou 450011, P. R. China

2. College of Planning and Architectural Engineering, Henan University of Science and Technology,Luoyang 471003, P. R. China

3. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, P. R. China

1 Introduction

Due to its versatility and acceptability, steel-reinforced concrete is one of the most common materials for construction; the embedded steel is protected from corrosion by concrete.But the hydration heat results in tensile stress in cement paste due to restraint from the aggregates, which may induce micro-cracking or macro-cracking (Bordas et al. 2008; Rabczuk et al. 2008)and lead to steel corrosion when concrete is subjected to seawater because chlorine in seawater destroys the corrosion-inhibitive properties of non-buffered alkalis (Vassie 1984;Al-Gahtani and Maslehuddin 2002; Ahmad 2003). The volume of steel corrosion products is two to four times of the original steel. The subsequent stress evolution may lead to the enlargement of concrete cracks, even structure failure. There are many examples of reinforced concrete structures that cannot remain durable in seawater for 30 years and more. To solve this problem, cooling plastic pipes are used to lower the temperature rise and to prevent cracking,because plastic pipes cannot be corroded by seawater and their prices are very cheap (Hedlund and Groth 1998; Li 2000; Liu et al. 2009; Deng and Murakawa 2006). This paper provides an introduction of a three-dimensional finite element program for thermal analysis of hydration heat in concrete structures with a plastic pipe cooling system, for analysis and design of hydraulic, coastal, and offshore engineering. The purposes of this study were to summarize the cooling results for the Cao’e Sluice and to validate the effect of plastic pipe cooling.

2 Finite element formulation

2.1 Equilibrium equation of heat transfer

A mass concrete structure that generates internal heat due to hydration can be subjected to various boundary conditions. Eq. (1)and the following boundary conditions govern the spatialtemporal variation of temperature (del Coz Diaz et al. 2008; Yaghi et al. 2006; Zhu 1998):

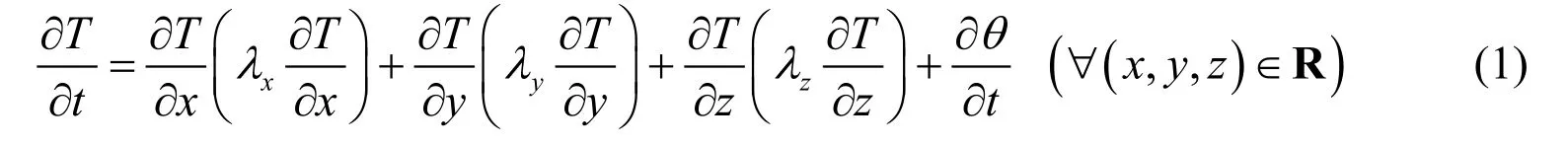
When t = 0,

where T is the transient temperature; T0is the initial temperature; t is time; λx, λy, and λzare, respectively, the thermal conductivities in the x, y, and z directions; and θ is the adiabatic temperature rise of concrete.

For boundary condition C1, the temperature Tbis known. This is a specified temperature condition, such as a constant source of heat:

For boundary condition C2, the adiabatic condition is satisfied, which means that the heat flux is equal to zero through the boundary:

where n is the outer normal direction of the boundary.

For boundary condition C3, the heat flux generated by atmosphere and cooling water convection is represented as

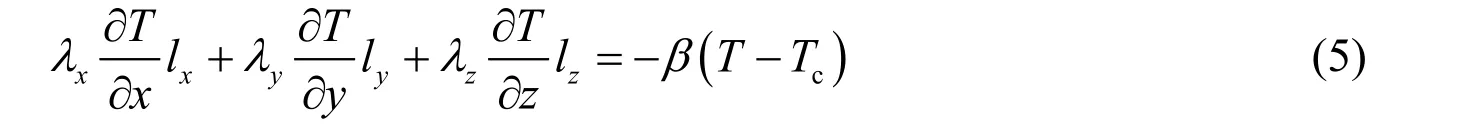
where β is the coefficient of heat convection for the atmosphere or cooling water, Tcis the concrete temperature on the convection boundary surface, and lx, ly, and lzare the direction cosines of the outer normal of the boundary.

The heat transfer problem can be solved using the three-dimensional finite element method. The equation for the method is (Zhu 1998)

where H is the matrix of heat conductivity, R is the added matrix for heat conductivity, Fm+1is the total heat flux vector for internal hydration heat and heat convection at time tm+1, Tmand Tm+1are the temperature matrices at time tmand tm+1, respectively, and the time interval between them is Δtm.

Therefore, if the temperature at time tmis known, then the temperature at time tm+1can be calculated with Eq. (6). When T0is known, the temperature at any time can be calculated.

2.2 Formulation of internal flow

The variation of the concrete temperature induced by hydration heat is controlled by circulating the cooling water through plastic pipes embedded in concrete. The outlet temperature of cooling water is mostly higher than the inlet temperature when the hydration heat of concrete is absorbed by the cooling water. This phenomenon is called heat transfer through internal flow. To calculate the temperature distribution of cooling water along the pipe,the energy conservation principle was used, which means that the heat supplied to the pipe is equal to the heat absorbed by the flowing water. In general, the temperature increment of internal flow ΔTwiis shown in Eq. (7)(Zhu and Xu 2003):

where λ is the thermal conductivity, cwis the specific heat of water, ρwis the density of water, qwis the inflow rate of water, s is the area along the cooling pipe, and Γ0is the boundary of pipe.

If the temperature of water at the inlet is known, the unknown temperature of the cooling water along the pipe can be calculated with Eq. (7).

2.3 Formulations of strain and stress

In the numerical process for stress analysis, the strain was calculated first, and then the corresponding stress could be obtained. If the time interval [t0, t]is subdivided into K steps,the strain increment Δεkat a typical step [tk-1,tk](k =1,2,… ,K)can be expressed as

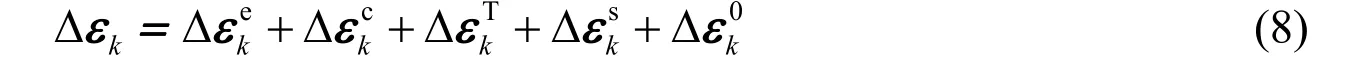
After the strain increment is calculated, the corresponding stress increment Δσkcan be obtained:

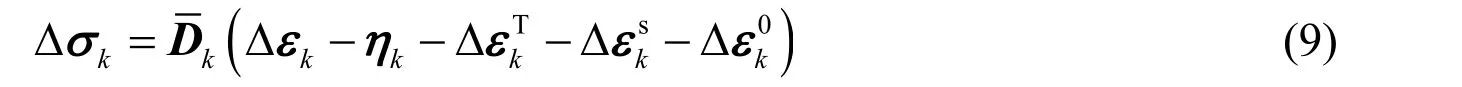
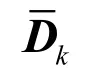
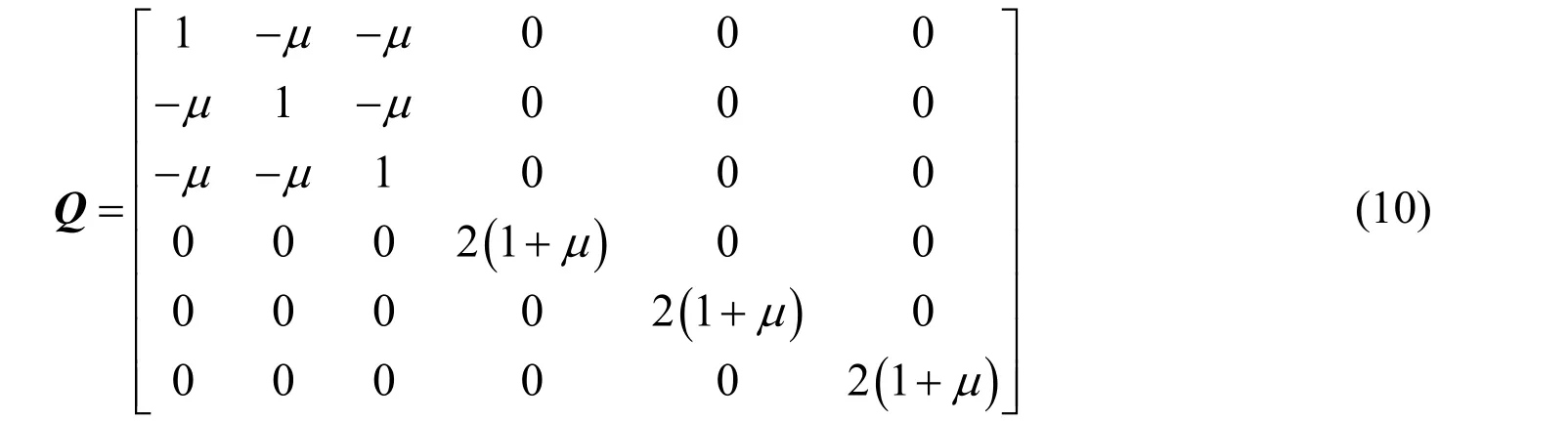
where µ is Poisson’s ratio.

The total stress at the moment of the kth step is

where σk-1is the total stress at the (k-1)th step.

3 Application of cooling pipe in Cao’e Sluice

3.1 Background of Cao’e Sluice

The estuary of the Qiantang River is a typical tidal estuary with a strong current and large tidal range that have caused serious damage to the sea dikes on both banks. The Cao’e Sluice, a hydraulic project constructed to solve this problem, is known as China’s first sluice of a tidal estuary for its large-scale and complicated conditions.

The spread footing is a concrete structure placed on the rock foundation. A footing was cast once on December 1, 2005. After 20 days, a sluice pier was cast with two lifts and the heights of the two lifts were both 0.4 m. The geometrical layout is illustrated in Fig. 1. The layout of the pipe loop was located at the center the sluice pier. There were 12 layers of pipes in all, and the first layer of pipes was laid 0.2 m above the footing. The distance between each group of cooling pipes was 0.4 m. Feature points S1 through S4 are also shown in Fig. 1, in which S1 is the surface point and other points are located in the concrete.

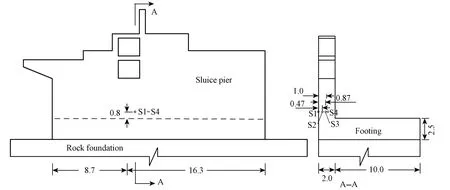
Fig. 1 Size of sluice and layout of feature points (unit: m)

The footing and pipe loop were modeled as shown in Fig. 2 by using eight-node isoperimetric solid elements. The dimension of rock was considered to be 45 m × 24 m × 6 m to simulate the effect of heat transferring from placed concrete to rock. As the temperature gradient of rock was smaller than that of the placed concrete, the mesh of the placed concrete was generated more finely than that of the rock. Hence, the total number of solids of the finite element mesh is 21 719 and the total number of nodes is 26 177.

Fig. 2 FEM mesh for simulation

3.2 Properties of materials

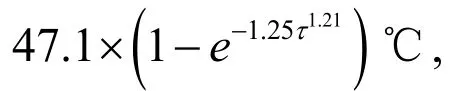
Table 1 Thermal properties of materials

The concrete of the sluice pier was mixed with 138.3 kg/m3of ordinary Portland cement(CEM I 42.5), 241.0 kg/m3of milled slag, and 1 308 kg/m3of limestone aggregate, and the concrete has a water/cement ratio of 0.41. The 28-day split concrete tensile strength obtained by in situ tests was 3.72 MPa, with a safety factor of 1.65. That is, the allowed 28-day tensile strength was 2.3 MPa. The creep compliance model is shown as follows:

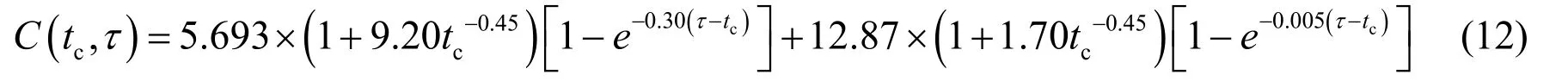
where tcis the age of concrete at the time of loading.

3.3 Results and discussion

With the three-dimensional finite element program, the construction process of the Cao’e Sluice with no pipe cooling system and dynamically updated geometry of the FEM mesh were simulated, and the temperature and stress of the sluice pier were analyzed. Fig. 3 shows the temperature history of the feature points. The temperature increased due to the hydration heat(Song et al. 2006; Mo and Deng 1998), and reached its maximum value at about two days after casting. Because of the heat transferring from concrete to the outside air, the peak temperature was less than the sum of the initial temperature and the adiabatic hydration temperature rise.After two days, the block began to cool down, but still required a long time to reach the environmental temperature. The peak temperature occurred at point S4 because point S4 was located on the centerline of the section and was far away from the heat dispersing surface.Fig. 4 shows the variation of stress at the same points of the sluice pier. At first, a compression stress developed inside the block and a tensile stress developed on the surface; this is because concrete tended to expand due to the temperature rise, while the boundary conditions restricted its expansion. The maximum compression stress also occurred at about one day after the sluice pier was cast. Compression stress decreased as expected because the block began to cool down.Finally, the compression stress changed to tensile stress and the tensile stress became increasingly large and exceeded the allowed tensile strength (2.3 MPa). Thus, cracks may have appeared. Cracks accelerate steel corrosion because steel is subjected directly to seawater, then,corrosion products cause the concrete to crack seriously, and the concrete structure may be damaged.

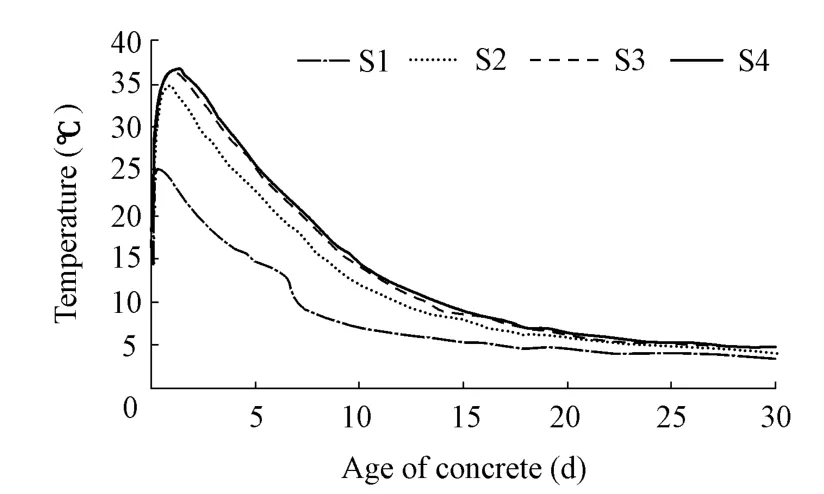
Fig. 3 Temperature of feature points without pipe

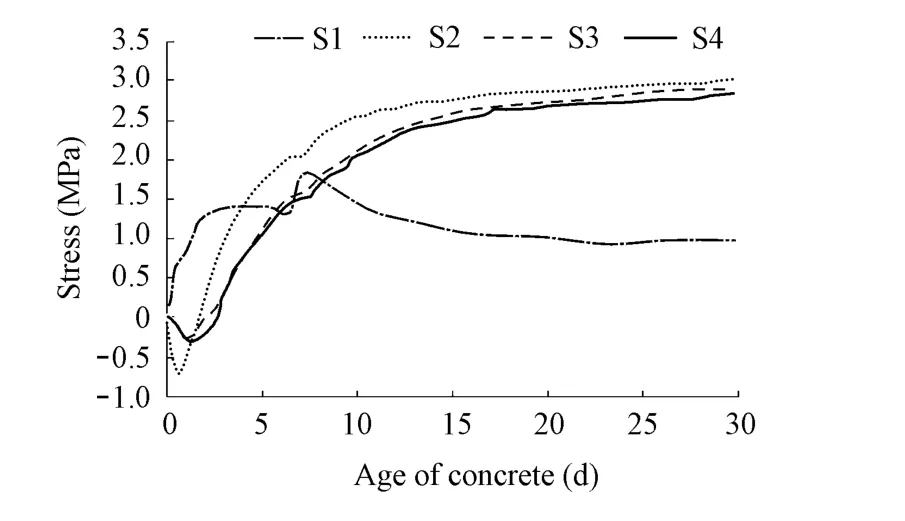
Fig. 4 Stress of feature points without pipe

The temperature histories of concrete with plastic pipe at the feature points due to the hydration heat are presented in Fig. 5. The figure shows that the temperature of concrete with the pipe cooling system decreases more rapidly than the non-cooled concrete, and the peak temperature at the feature points with pipe is less than that without pipe. This trend is much more apparent at point S3, which is at a location close to cooling pipe. In the cooled concrete,however, the stress did not reach the allowed tensile strength, 2.3 MPa, either before or after the stripping of forms (Fig. 6). The disconnection of the water after five days can be found for the cooled cases, but did not cause any increase in the risk of cracking.

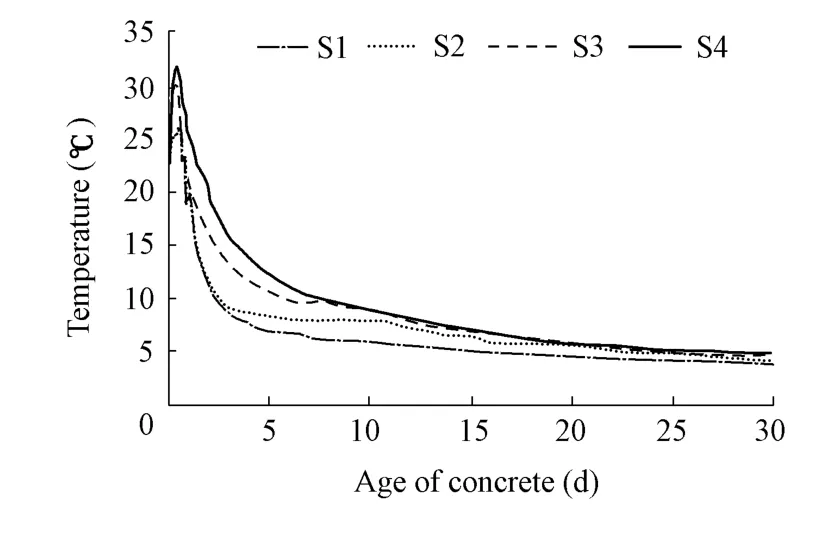
Fig. 5 Temperature of feature points with pipe

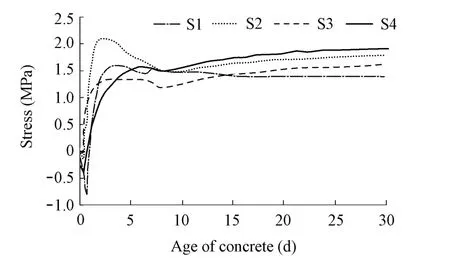
Fig. 6 Stress of feature points with pipe

Fig. 7 shows the possible critical zones at the longitudinal section. In general, the tensile stress at interface corners and the footing area where cracks usually occur is more commonly than that in other areas, but the stress does not reach the allowed tensile strength. That is to say,the plastic pipe cooling system is applicable to preventing cracking.

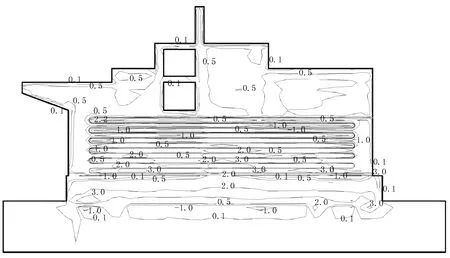
Fig. 7 Profile of concrete stress with plastic pipes at 30th day (unit: MPa)

4 Conclusions

A dynamic computer simulation of a sluice with and without cooling pipe system has been presented in this paper. The level of thermal stress in the construction was significantly improved by embedded cooling water. The following conclusions can be drawn:

(1)In general, the cooling effect of steel pipes is better than that of plastic pipes, but plastic pipes cannot be corroded by seawater and have the properties of good flexility and low price; therefore, they are usually used for temperature control. Results in this paper show that plastic pipes have the ability to reduce the temperature rise effectively, and that the maximum temperature at all feature points of concrete without plastic pipes is 3.5℃ higher than that at the same feature points of concrete embedded with pipes.

(2)The thermal stress of concrete without plastic pipes is larger than that with pipes,preventing the Cao’e Sluice from cracking. Post-cooling of concrete with plastic pipes is applicable to cracking prevention in hydraulic, coastal, and offshore engineering.

Ahmad, S. 2003. Reinforcement corrosion in concrete structures, its monitoring and service life prediction: A review. Cement and Concrete Composites, 25(4-5), 459-471. [doi:10.1016/s0958-9465(02)00086-0]

Al-Gahtani, A. S., and Maslehuddin, M. 2002. Characteristics of the Arabian gulf environment and its impact on concrete durability: An overview. Proceedings of the 6th Saudi Engineering Conference, 169-184.Dhahran: King Fahd University of Petroleum and Minerals.

Bordas, S., Rabczuk, T., and Zi, G. 2008. Three-dimensional crack initiation, propagation, branching and junction in non-linear materials by an extended mesh free method without asymptotic enrichment.Engineering Fracture Mechanics, 75(5), 943-960. [doi:10.1016/j.engfracmech.2007.05.010]

del Coz Diaz, J. J., Garcia Nieto, P. J., Suarez Sierra, J. L., and Penuelas Sanchez, I. 2008. Non-linear thermal optimization and design improvement of a new internal light concrete multi-holed brick walls by FEM.Applied Thermal Engineering, 28(8-9), 1090-1100. [doi:10.1016/j.applthermaleng.2007.06.023]

Deng, D., and Murakawa, H. 2006. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Computational Materials Science, 37(3), 269-277. [doi:10.1016/j.mcn.2008.03.006]

Hedlund, H., and Groth, P. 1998. Air cooling of concrete by means of embedded cooling pipes, Part I:Laboratory tests of heat transfer coefficients. Materials and Structures, 31(5), 329-334.[doi:10.1007/BF02480675]

Li, R. C. 2000. Field test on cooling water plastic pipes for Three Gorges Dam. China Three Gorges Construction, (5), 20-23. (in Chinese)

Liu, X. Q., Li, T. C., and Han, B. 2009. Direct algorithm for simulating cooling effect of water pipes in concrete. Journal of Hydraulic Engineering, 40(7), 892-896. (in Chinese)

Mo, L. W., and Deng, M. 2006. Thermal behavior of cement matrix with high-volume mineral admixtures at early hydration age. Cement and Concrete Research, 36(10), 1992-1998. [doi:10.1016/j.cemconres.2006.07.002]

Rabczuk, T., Zi, G., Bordas, S., and Nguyen-Xuan, H. 2008. A geometrically non-linear three-dimensional cohesive crack method for reinforced concrete structures. Engineering Fracture Mechanics, 75(16),4740-4758. [doi:10.1016/j.engfracmech.2008.06.019]

Song, H. W., Kwon, S. J., Byun, K. J., and Park, C. K. 2006. Predicting carbonation in early-aged cracked concrete. Cement and Concrete Research, 36(5), 979-989. [doi:10.1016/j.cemconres.2005.12.019]

Vassie, P. 1984. Reinforcement corrosion and the durability of concrete bridge. Ice proceedings, 713-723.Hamburg: Der Versuchsanstalt.

Yaghi, A., Hyde, T. H., Becke, A. A., Sun, W., and Williams, J. A. 2006. Residual stress simulation in thin and thick-walled stainless steel pipe welds including pipe diameter effects. International Journal of Pressure Vessels and Piping, 83(11-12), 864-874. [doi:10.1061/(ASCE)0733-9372(2007)133:4(447)]

Zhu, B. F. 1998. Thermal Stresses and Temperature Control of Mass Concrete. Beijing: China Electric Power Press. (in Chinese)

Zhu, Y. M., and Xu, Z. Q. 2003. A calculation method for solving temperature field of mass concrete with cooling pipes. Journal of Yangtze River Scientific Research Institute, 20(2), 19-22. (in Chinese)